过程内分析 Intraprocedural Analysis
定义 definition
在过程内分析中,我们会对程序和标签进行一定处理。和RDentry RDexit类似,我们将程序每一句代码执行划分成初始和结束。分别用 init : Stmt -> Lab ,final : Stmt -> f (Lab)表示。
将代码块本身用 blocks( ) 表示,同时给予方程定义 对代码块进行细化分解。对独立语句用{ } 包裹,对复杂语句依旧用 blocks( ) 表示,同时对细化后的结果进行并运算。
此时,我们可以对某一个代码执行过程进行描述 : Labels(S) = { l | [B]^l ∈ blocks(S)}
执行完 S 代码后,所有数据构成的表格 由进入该语句前数据表格和执行过程中改变的数据表格组成。也就是说 Label 由 init 和 final 共同组成。
流 flows
一如之前的思路,描述完语句之后,还要描述语句之间的逻辑关系。而流就是数据流分析的逻辑关系。面对单纯赋值的语句或者没有操作的语句,它的流就是空。面对代码块,它的流包括代码的执行流,以及输入输出流。
至此,数据流分析的构成要素已经全部提出。
一个例子 An example
我们来用一个例子加深理解

我们将这整个流程图看作一个整体进行分析。用Example作为整段代码的标签。
首先简单用标签作方程右值
init(Example) = 1 final(Example) = {2} Labels(Example) = {1,2,3,4}
将流简单的表示为集合 {(1,2),(2,3),(3,4),(4,2)}
接下来进行方程化
Labels (Example) = {init(Example)} ∪ { l | ( l , l' ) ∈ flow(Example) } ∪ { l' | ( l , l' ) ∈ flow(Example)}
一眼看上去可能会疑惑为什么是这样,我们来分析一下。
Labels 是 包含整个代码执行过后各变量值的表格
而变量由进入该流程前的表达式以及流程内部表达式决定。也就是说,Labels = init ∪ flow
flow是由(1,2),(2,3),(3,4),(4,2)组成的集合输入是1,输出是2。我们将while do和z:=1分开,flow (z:=1) = 空 flow(while do ) = flow (3,4) ∪ { ( 2,init (3,4) ) } ∪ { ( final(3,4) , 2 ) }
flow(3 , 4) = flow(3) ∪ flow(4) ∪ { final(3) , init(4) }
flow(Example) = { final(3) , init(4) } ∪ { ( 2,init (3,4) ) } ∪ { ( final(3,4) , 2 ) }
上面等式右侧六个元素是程序运行过程中记录改变的变量的表格
也就是说最终的labels会包含这六个表格的一个或两个或零个
整合起来就是Labels (Example) = {init(Example)} ∪ { l | ( l , l' ) ∈ flow(Example) } ∪ { l' | ( l , l' ) ∈ flow(Example)}
可用表达式分析 Available Expressions Analysis
这个时候,我们完成了对一段代码块或者一个程序的代码逻辑上的一个分析与简化。接下来,我们对代码具体内容进行一个简化。
我们可以想象这样一种场景,当a+b被多次当作右式赋值给不同的变量,我们是否需要多次重复这一个算式运算。答案显然是不需要,只要计算一次结果,那么a+b的结果就已知了。但是这个时候又会出现另一种情况,当a或者b在流程中被改变了,那么a+b的值也会发生变化。那么我们究竟要不要对像a+b这样的多次重复表达式进行简化呢。我们又如何对他进行简化呢.
同样以一串简单代码为例
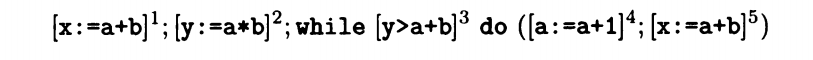
当语句1计算完a+b结果后,第一次3所代表的循环判断不需要被计算了,当4语句执行后5所代表的a+b需要被重新计算,而同时3所代表的循环判断又不需要进行计算了。
显然之前的描述方式中没有能够描述这样一个a+b变量的表达,但正如我们可以用v表达任一单一变量,我们可以用一个新的符号表示像a+b这样的作为整体可以看作是变量的变量运算。AExp就是人们想到的符号。同时,为了不忽视像 a 和 b 这样作为运算式成员的变量,我们用AExp(v)来表示这些变量。
接下来,我们要对a+b是否变化进行判断,当a或者b变化时,我们需要重新计算,也就是抛弃我们之前的计算,而在下一次计算时,我们会重新定义a+b的结果。
所以,我们对AExp的动作进行定义,kill和generate 即消灭和生成
由于分析器不能直观辨别出下一句代码是否会对a或者b进行操作,所以我们对每一句代码都要进行对AE 的定义,依照惯例,我们对每一句代码的开始和结束两个状态进行定义。AE entry ( l ) 和AE exit ( l )
以上面的代码为例子对AE entry 和AE exit 进行描述
对1描述如下: AE entry (1) = 空
AE exit (1) = gen AE (x:=a+b) ∪ AE entry (1)
对2描述如下: AE entry (2) = AE exit (1)
AE exit (2) = gen AE (y:=a*b) ∪ AE entry (2)
对3描述如下:AE entry (3) = AE exit (2) ∩ AE exit (5)
AE exit (3) = AE entry (3)
对4 描述如下: AE entry (4) = AE exit (3)
AE exit(4) = AE entry (4) \ kill AE (a+b , a*b , a+1)
对5描述如下: AE entry (5) = AE exit (4)
AE exit (5) = gen AE (x:=a+b) ∪ AE entry (5)
总结如下:
AE entry (l) = 空 (当 l = init(S) ) / ∩{AE exit (l') | ( l' , l ) ∈ flow (S) } (其他情况)
AE exit (l) = (AE entry(l)\kill AE (B^l) ) ∪ gen AE (B^l)
结果表达式分析 (根据理解自己翻译的) Reaching Definition Analysis
kill和gen 除了能够描述可用表达式的生成与改变,也可以用于变量的生成与改变,从而判断程序结束时,变量最终结果。因此,我们参照上面对于可用表达式的描述以下面的代码为例对参数也进行相似的描述。

RD entry (1) = { (x,?) , (y,?) }
RD eixt (1) = RD entry (1) \ kill RD { (x,?) , (x,1) (x,5) } ∪ gen RD (x,1)
RD entry (2) = RD exit (1)
RD eixt (2) = RD entry (2) \ kill RD { (y,?) , (y,2) (y,4) } ∪ gen RD { (y,2) }
RD entry (3) = RD exit (2) ∪ RD exit (5)
RD eixt (3) = RD entry (3)
RD entry (4) = RD exit (3)
RD eixt (4) = RD entry (4) \ kill RD { (y,?) , (y,2) (y,4) } ∪ gen RD { (y,4) }
RD entry (5) = RD exit (4)
RD eixt (5) = RD entry (5) \ kill RD { (x,?) , (x,1) (x,5) } ∪ gen RD { (x,5) }
这个时候我们就可以明确的知道程序最后每个变量的值是多少。
必定使用表达式分析 (个人理解的翻译) Very Busy Expressions Analysis
不知道大家有没有注意到,我们目前在数据流分析这一专题中举的例子都是while循环,没有出现过if。if和while有什么区别呢。while是真则做操作循环重复,if是真假各有分支,只做一次。也就是说针对while的可用表达式分析,对于if来说似乎并不是那么有用。
但是对于if来说是不是就不存在可重复使用的表达式呢。在某种情况下,还是存在的。比如说下图中的代码
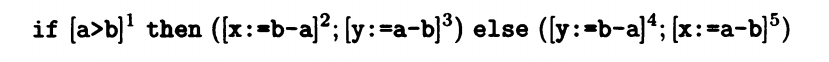
无论a是否大于b ,a-b和b-a都会被使用,只不过赋给了不同的变量。在这一段代码中,与之前的while的单一输入多种输出不同,if相较于输出,输入更加具有不确定性。对于程序的分析而言,我们需要知道的就是那些输入会进入yes分支,那些会进入no分支,所以我们从输出向输入分析,也叫做逆流分析。
我们可以列出以下表达式:
VB entry (1) = VB exit (1)
VB entry (2) = VB exit (2) ∪ {b-a}
VB entry (3) = VB exit (3) ∪ {a-b}
VB entry (4) = VB exit (4) ∪ {b-a}
VB entry (5) = VB exit (5) ∪ {a-b}
由于 VB exit(5) 和 VB exit (3) 都是这一代码块的最终输出,对这一代码块的执行没有影响,所以VB exit(5) 和 VB exit (3)都是空,也就是说,VB entry (3) = VB exit (3) ∪ {a-b}和VB entry (5) = VB exit (5) ∪ {a-b}都可以改写为 VB entry (3) = {a-b} , entry (5) = {a-b}
同样的,我们对VB exit (l) 进行定义:
VB exit (1) = VB entry (2) ∩ VB entry (4)
VB exit (2) = VB entry (3)
VB exit (3) = 空
VB exit (4) = VB entry (5)
VB exit (5) = 空
活变量分析 Live Variables Analysis
活变量是在使用之前只经过一次定义赋值的变量。分析活变量有什么意义呢?
我们先分析一下再做评论。以下图代码为例:
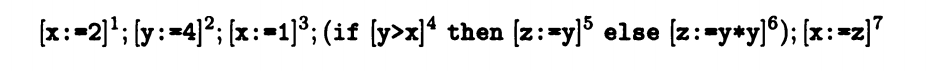
上面的代码具有一个输入两个分支以及一个必定使用的表达式的特征,正向分析和逆向分析都可以,我们也可以对比一下两者的不同。
正向分析:
LV entry (1) = 空
LV exit (1) = LV entry (1) ∪ gen LV (x:=2)
LV entry (2) = LV exit (1)
LV exit (2) = LV entry (2) ∪ gen LV (y:=4)
LV entry (3) = LV exit (2)
LV exit (3) = LV entry (3) \ kill LV (x:=2) ∪ gen LV (x:=1)
LV entry (4) = LV exit (3)
LV exit (4) = LV entry (4)
LV entry (5) = LV exit (4)
LV exit (5) = LV entry (5) ∪ gen LV (z:=y)
LV entry (6) = LV exit (4)
LV exit (6) = LV entry (6) ∪ gen LV (z:=y*y)
LV entry (7) = LV exit (5) ∪ LV exit (6)
LV exit (7) = LV entry (7) \ kill LV (x:=2,x:=1) ∪ gen LV (x:=z)
逆向分析:
LV entry (1) = LV exit (1) \ kill LV (x:=2)
LV exit (1) = LV entry (2)
LV entry (2) = LV exit (2) \ kill LV (y:=4)
LV exit (2) = LV entry (3)
LV entry (3) = LV exit (3) \ kill LV (x:=1)
LV exit (3) = LV entry (4)
LV entry (4) = LV exit (4)
LV exit (4) = LV entry (5) ∪ LV entry (6)
LV entry (5) = LV exit (5) \ kill LV (z:=y)
LV exit (5) = LV entry (7)
LV entry (6) = LV exit (4) \ kill LV (z:=y*y)
LV exit (6) = LV entry (7)
LV entry (7) = LV exit (7) \kill LV (x:=z)
LV exit (7) = 空
我们可以清晰的看到无论是流还是逆流,我们的入口都是空,其余的方程关系都可以通过移项实现转换,而不同之处就在于我们需要找的是入口的可能性还是出口的可能性。
接下来,我们要对方程进行化简。对于LV exit 我们不需要对形式化简,只需要求出LV entry。对于LV entry 我们忽视赋值表达式的右值的计算,只在意左值和右值分别使用的变量名。左值用 \ 右值用 ∪ 。我们可以对LV entry 进行如下改写:
LV entry (1) = LV exit (1) \ {x}
LV entry (2) = LV exit (2) \ {y}
LV entry (3) = LV exit (3) \ {x}
LV entry (4) = LV exit (4) ∪ {x,y}
LV entry (5) = LV exit (5) \ {z} ∪ {y}
LV entry (6) = LV exit (6) \ {z} ∪ {y}
LV entry (7) = LV exit (7) \ {x} ∪ {z}
再将 LV entry 和 LV exit 整合得到最简表示
LV entry (7) = {z}
LV entry (6) = {y}
LV entry (5) = {y}
LV entry (4) = {y} ∪{x,y}
LV entry (3) = {y}
LV entry (2) = 空
LV entry (1) = 空
LV exit (7) = 空
LV exit (6) = {z}
LV exit (5) = {z}
LV exit (4) = {y}
LV exit (3) = {y} ∪{x,y}
LV exit (2) = {y}
LV exit (1) = 空
这时我们可以看到第一句代码对这个程序没有任何影响,也就是说是一句可去代码。这也就是分析活变量的意义:找出死代码去除,简化程序。
派生数据流信息 Derived Data Flow Information
经过上面的活变量分析,我们可以发现实质上,活变量分析就是寻找定义和使用之间是否还含有重定义,如果有,那么这个定义就可以省略,而离使用最近的定义就是唯一有用的定义。既然如此,我们可以将定义和使用建立连接,从而对程序进行简化。 我们将定义连接使用称作UD chain 使用连接定义称作DU chain,将定义到使用的代码块用clear表示,clear 是包含 变量v , 定义语句标签 l ,使用语句标签 l' 的一个函数。
我们用use(x,l) 表示 x在标签为 l 的代码中被使用,def(x,l) 表示 x 在标签为x 的代码中被定义。
以下图为例理解UD链和DU链
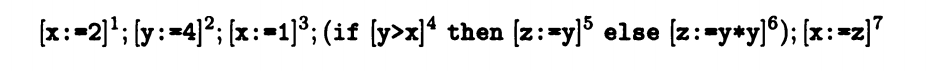
首先给出通用表达式
ud(x,l') = { l | def (x,l) ^ ヨl'‘ : (l,l'') ∈ flow(S) ^ clear (x,l'',l')} ∪ {? | clear(x,init(S),l')}
寻找第l' 的x是在哪里定义的,只需要找在S中的第一句到 l' 的语句中是否存在定义,同时在那一句之后到 l’ 是否没有被重定义。也就是表示为{ l | def (x,l) ^ ヨl'‘ : (l,l'') ∈ flow(S) ^ clear (x,l'',l')} 。如果从第一句开始,这个变量就没有被定义,那么这个变量就是在S之前的某一句定义的,也就是{? | clear(x,init(S),l')}。ud的 l' 是一句运算表达式 。l是运算表达式用到的变量的定义式
同样的给出DU链表达式
du(x,l) = {l' | def (x,l) ^ ヨ l'' : (l,l'') ∈ flow(S) ^ clear (x,l'',l') } 当l不等于?时
l 是一句定义句 ,从当前句往后找符合在S 中同时使用了x的 l‘ 记录
当 l 等于 ? 时 du(x,l) = {l' | clear(x,init(S),l')}
也就是针对S中使用但是没有在S中定义的变量所在语句。
从特殊的du(x,?)和使用x的那一句代码对应的 ud(x,l') 我们可以清楚的看到du和ud的关系: du(x,l) = { l' | l ∈ ud(x,l')}
最后给出上述例子的ud链和du链的表格,以提供读者验证。

理论证明 Theory
结构归纳法 structural induction
我们十分熟悉数学归纳法,数学归纳法是对一组无穷项的数列进行数据归纳的一种方式。结构归纳法与其类似,是对任意大小的结构进行归纳的一种方式。即:提出一个针对最小结构单元以及任意子结构都成立的命题
举一个例子
我们以二分查找算法为例:
存在一组有序数列3,4,5,7,2,1,6,8
第一次查找将数列分成两部分:3,4,5,7和2,1,6,8
第二次查找再细分:3,4 5,7 2,1 6,8
第三次查找: 3 4 5 7 2 1 6 8
每一次都将整体分成两个部分,直到最后只有一个最小单元。每一个子结构都满足最初结构的属性。这就是结构归纳法
结构上的操作语义 Structural Operational Semantics
而结构归纳法在程序分析中的应用就是将代码块分解成最小单元代码进行描述。在对结构描述之前,先对数理结构进行简单描述
数据类型
整型描述: A[x]σ = σ(x) 对于整数型操作语句 变量 x 为 σ(x)
A[n]σ = N[n] 对于整数型操作语句 值为N[n]
A[a1 opa a2]σ = A[a1]σ opa A[a2]σ 对于AExp的操作描述,将各元素描述后进行操作。
布尔型描述:B[not b]σ = ┐ B[b] σ 对于布尔型操作语句 not 用┐描述
B[b1 opb b2]σ = B[b1]σ opb B[b2]σ 对于大的布尔结构进行细化描述
B[a1 opb a2]σ = A[a1]σ opb A[a2]σ 对于最小的结构先对元素各自描述再对操作描述
之后对结构进行描述
对于结构的描述可以用<S,σ>表示,而对于一个结构,他可能是复杂结构或者是简单结构。也就是说,<S,σ> 的结果可能是一个确定的值,也可能是仍需要执行的S 以及已经得到的中间结果σ。
用符号表示:<S,σ> -> σ' and <S,σ> -> <S',σ'>
此时,我们可以对所有不同类型的语句进行描述:
对于赋值语句 x=a 可以描述成 \<[x:=a]^l , σ> -> σ[x -> A[a]σ ]
代码块 S1, S2 描述成 <S1,σ> --> <S1',σ'> | <S1;S2,σ> --> <S1';S2,σ'> (S1为复杂语句,执行一步后,得到σ‘ ,剩余S1部分和S2 当作新的整体)
也可以能是<S1,σ> --> σ' | <S1;S2,σ> --> <S2,σ'> (S1是简单语句,一步执行可以完成所有操作 )
面对判断语句 我们描述为 <if [b]^l then S1 else S2 , σ> --> <S1,σ> 当真时
<if [b]^l then S1 else S2 , σ> --> <S2,σ> 当假时
面对while语句 我们描述为 \<while [b]^l do S, σ \> --> <(S;while [b]^l do S ),σ> 当真时
<while [b]^l do S ,σ > --> σ 当假时
我们来对下面一个例子进行尝试

< [x:=5]^1 ; [y:=1]^2 ; while [x>1]^3 do ([y:=x\*y]^4 ; [x:=x-1]^5 ) , σ>
--》 < [y:=1]^2 ; while [x>1]^3 do ([y:=x\*y]^4 ; [x:=x-1]^5 ) , σ’>
--》< while [x>1]^3 do ([y:=x\*y]^4 ; [x:=x-1]^5 ) , σ‘’>
--》 < [y:=x\*y]^4 ; [x:=x-1]^5 while [x>1]^3 do ([y:=x\*y]^4 ; [x:=x-1]^5 ) , σ‘’>
--》< [x:=x-1]^5 while [x>1]^3 do ([y:=x\*y]^4 ; [x:=x-1]^5 ) , σ‘’’>
--》 < while [x>1]^3 do ([y:=x\*y]^4 ; [x:=x-1]^5 ) , σ‘’‘‘>
--》 σ’‘’‘’
再运用之前所学到的流,将这一完整结构代码细化:
<S, σ> --> σ' 用流的知识可以表示为 final(S) = {init(S)}
<S, σ> --> <S',σ'> final (S) 被包含于 final(S')
flow(S) 被包含于 flow(S')
blocks(S) 被包含于 blocks(S')
此时我们是否可以用结构归纳法对上述描述进行归纳
活变量正确性证明 Correctness of Live Variable Analysis
证明活变量是正确的只需要证明确实只有活变量才对我们程序运行结果产生影响。
我们从特殊到一般,首先用x=y+z来考虑:
我们令V1={y,z} V2={x},同时用~表示相等关系:σ1 ~v1 σ2 ( σ1(y,z) = σ2(y,z) )
显然,当σ1 ~v1 σ2 时σ1 ~v2 σ2也成立。也就是说 ~ 的关系不会因为计算而改变。因此我们将计算前和计算后状态分开,分别用N,X表示。N(l) = live entry (l) X(l) = live exit (l)
同时,由于~不会改变,只要在一段代码执行中活变量依旧是活变量,结果就不会改变,用符号表示就是:σ1 ~X(l) σ2 --> σ1 ~N(l') σ2 所以只有活变量才会对程序运行结果有影响。也就是说:<S,σ1> --> <s',σ1'> σ1 ~N(init(S)) σ2就会有σ2’满足<S,σ2> --> <s',σ2'> σ1‘ ~N(init(S‘)) σ2’
<S,σ1> --> σ1' σ1 ~N(init(S)) σ2就会有σ2’满足<S,σ2> --> σ2' σ1‘ ~X(l) σ2’
框架 Frameworks
我们回过头来看之前讲的可用表达式分析,必定使用表达式分析,结果表达式分析,活变量分析来寻找其中共性搭建一个框架。
可用表达式分析,我们当时做出了以下结论
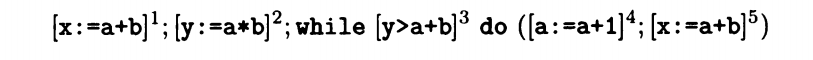
AE entry (1) = 空
AE exit (1) = gen AE (x:=a+b) ∪ AE entry (1) = gen AE (x:=a+b)
AE entry (2) = AE exit (1) = gen AE (x:=a+b)
AE exit (2) = gen AE (y:=a*b) ∪ gen AE (x:=a+b)
AE entry (3) = AE exit (2) ∩ AE exit (5) = gen AE (y:=a*b) ∪ gen AE (x:=a+b) ∩ AE exit (5)
AE exit (3) = AE entry (3) = gen AE (y:=a*b) ∪ gen AE (x:=a+b) ∩ AE exit (5)
AE entry (4) = AE exit (3) = gen AE (y:=a*b) ∪ gen AE (x:=a+b) ∩ AE exit (5)
AE exit(4) = AE entry (4) \ kill AE (a+b , a\*b , a+1) = AE exit (5) \ kill AE (a+b , a\*b , a+1)
AE entry (5) = AE exit (4) = AE exit (5) \ kill AE (a+b , a\*b , a+1)
AE exit (5) = gen AE (x:=a+b) ∪ AE entry (5) = gen AE (x:=a+b) ∪ AE exit (5) \ kill AE (a+b , a\*b , a+1)
我们可以看到 AE entry (3) 是交集,也就是说半序集的逻辑关系是交集,每一次循环的结果都是上一次循环的子集,属于被包含关系,下限是所有表达式的解,上限是空
结果表达式分析

RD entry (1) = { (x,?) , (y,?) }
RD eixt (1) = RD entry (1) \ kill RD { (x,?) , (x,1) (x,5) } ∪ gen RD (x,1)
RD entry (2) = RD exit (1)
RD eixt (2) = RD entry (2) \ kill RD { (y,?) , (y,2) (y,4) } ∪ gen RD { (y,2) }
RD entry (3) = RD exit (2) ∪ RD exit (5)
RD eixt (3) = RD entry (3)
RD entry (4) = RD exit (3)
RD eixt (4) = RD entry (4) \ kill RD { (y,?) , (y,2) (y,4) } ∪ gen RD { (y,4) }
RD entry (5) = RD exit (4)
RD eixt (5) = RD entry (5) \ kill RD { (x,?) , (x,1) (x,5) } ∪ gen RD { (x,5) }
现在我们对所有表达式进行计算从而得出最终结果
RD entry (1) = { (x,?) , (y,?) }
RD eixt (1) = { (x,1),(y,?) }
RD entry (2) = { (x,1),(y,?) }
RD eixt (2) = { (x,1),(y,2)}
RD entry (3) = { (x,1),(y,2) }
RD eixt (3) = { (x,1),(y,2) }
RD entry (4) = { (x,1),(y,2) }
RD eixt (4) = { (x,1),(y,4) }
RD entry (5) = { (x,1),(y,4) }
RD eixt (5) = { (x,5),(y,4) }
RD entry (3) = { (x,5),(y,4) }
RD eixt (3) = { (x,5),(y,4) }
RD entry (4) = { (x,5),(y,4) }
RD eixt (4) = { (x,5),(y,4) }
RD entry (5) = { (x,5),(y,4) }
RD eixt (5) = { (x,5),(y,4) }
我们可以看到运行过程中,每一句改变x,y的代码都发挥了作用。最后的结果是经过共同处理的结果。也就是说,半序集的逻辑关系是并集,每一次循环的结果都包含于下一次循环,下限是空,上限是所有表达式的结果
必定使用表达式分析
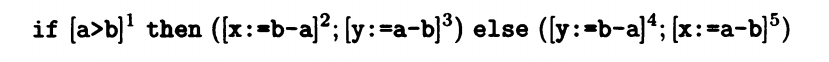
VB exit (1) = VB entry (2) ∩ VB entry (4)
VB exit (2) = VB entry (3)
VB exit (3) = 空
VB exit (4) = VB entry (5)
VB exit (5) = 空
VB entry (1) = VB exit (1) = {a-b} ∪ {b-a} ∩ {a-b} ∪ {b-a}
VB entry (2) = VB exit (2) ∪ {b-a} = {a-b} ∪ {b-a}
VB entry (3) = VB exit (3) ∪ {a-b} = {a-b}
VB entry (4) = VB exit (4) ∪ {b-a} = {a-b} ∪ {b-a}
VB entry (5) = VB exit (5) ∪ {a-b} = {a-b}
这里,我们使用了逆流分析,init(S) 是 VB exit(5) final(S) = VB entry (1)
我们可以看到结果是交集,也就是说半序集逻辑关系是交集,属于被包含关系。下限是所有表达式结果。
活变量表达式
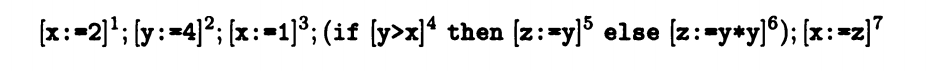
我们选择逆流分析
LV entry (1) = LV exit (1) \ kill LV (x:=2)
LV exit (1) = LV entry (2)
LV entry (2) = LV exit (2) \ kill LV (y:=4)
LV exit (2) = LV entry (3)
LV entry (3) = LV exit (3) \ kill LV (x:=1)
LV exit (3) = LV entry (4)
LV entry (4) = LV exit (4)
LV exit (4) = LV entry (5) ∪ LV entry (6)
LV entry (5) = LV exit (5) \ kill LV (z:=y)
LV exit (5) = LV entry (7)
LV entry (6) = LV exit (4) \ kill LV (z:=y*y)
LV exit (6) = LV entry (7)
LV entry (7) = LV exit (7) \kill LV (x:=z)
LV exit (7) = 空
LV entry (7) = {z}
LV entry (6) = {y}
LV entry (5) = {y}
LV entry (4) = {y} ∪{x,y}
LV entry (3) = {y}
LV entry (2) = 空
LV entry (1) = 空
LV exit (7) = 空
LV exit (6) = {z}
LV exit (5) = {z}
LV exit (4) = {y}
LV exit (3) = {y} ∪{x,y}
LV exit (2) = {y}
LV exit (1) = 空
我们可以看到在没有求最终结果的 LV exit(4) 是并集关系,也就是说半序集逻辑关系是并集,属于包含关系。下限是空。
这四种分析方法所建立的模型都是单调的,或单调递增或单调递减,也就是说我们要构建的框架是单调的
建立框架后,我们需要找到通过框架研究问题的方法。对于单调函数并且每一次函数的因变量都是下一次函数的自变量,我们可以选择迭代的方法寻找问题的解。
流程为:初始化流以及标签等需要使用到的数组集合或者表格。每执行一句代码对这些数据进行更新,最后输出结果。
用可用表达式分析的例子来演示
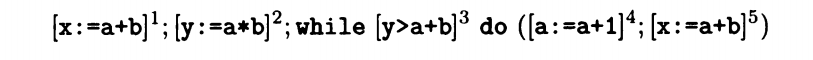
对于这一段代码,它的流是{(2,3),(3,4),(4,5),(5,3)},使用到的表达式是a+b,a*b,a+1。我们用U来表示这三个表达式的集合{(a+b),(a\*b),(a+1)}
迭代必须有出口,我们先证明结果存在:从理论上,假设有b行代码,有b^2个元素且是满射关系。每一次迭代的最后结果只可能是改变一个变量或者是增加b个变量。对于一个有限的集合,当每一次都增加b个变量时,最后一定会因为达到满集而终止。也就是之前提到的RD = f (RD)。
从上面的例子出发,不断迭代会发现a+b的极限只能是y,也就是x=y=a+b所以确实存在出口,就像使用迭代方法计算阶乘,最后一次循环1的阶乘是1.
接下来验证结果的正确性,也就是正确结果确实存在于集合中:首先,每一次进入这一段代码的数据集合总是包含于所有进入这一段代码可能的数据集合。每一次代码操作可能去除或者新增数据。对于去除的操作,每一次的结果都包含于原先的集合。对于新增,我们可以把新的数据集合表示为原数据集合并上这一次对应函数关系所对应的结果,他一定是包含于所有可能的集合并上上一次所有可能的集合对应同样的函数关系得到的结果。无论如何,不会有大于包含所有可能性集合的集合。也就是说,所有可能的结果都在分析的结果中。
除了迭代法以外,还有一种方式可以计算结果,那就是遍历法,把所有路径全部走一遍。这一方法的结果必定是全部结果并且没有不可能的结果。如同我们在可计算的验证之中提到的,迭代法的结果是近似值,而遍历法不会是近似值,因为如果程序最终崩溃无法得到结果,这一路径就是错误路径,也就不属于结果中的一员。遍历法会在后面的过程间分析使用到。




