过程间分析 interprocedural
在之前，我们介绍的都是一些简单的代码块，没有涉及函数的调用等复杂情况，接下来，我们学习过程间分析的一些技术来实现对复杂情况的研究。
对一个程序，我们用P来表示，对于程序中变量的声明用D表示，对变量的调用用S表示。我们可以简单的将begin和end作为程序开头结尾的标志。
对于变量声明语句，我们记录变量名，以及变量对应的作用域。我们用proc p(val x,res y) is^l_n S end^l_x 来表示。其中x表示调用变量，y表示结果变量，is表示开端，end表示结尾，l_n,l_x分别表示开端结尾语句的标签。
对于调用语句，我们必须知道调用的语句位置在哪，结果返回到哪个语句，我们用l_c表示调用语句位置，l_r表示结果返回语句位置。同时用call p(x,y)对调用的声明语句进行记录。完整表述是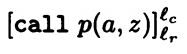
我们接下来使用流的思想，对程序进行分析：
先单独对调用部分分析
init(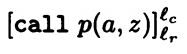) = l_c
final(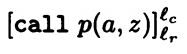) = l_r
blocks()= {}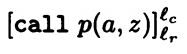
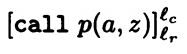labels(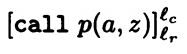) = {l_c,l_r}
flow(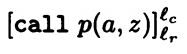) = {(l_c;l_n),(l_x;l_r)}
(l_c;l_n) 代表进入p之前的数据流
(l_x;l_r) 代表退出p之后的数据流
之后结合调用部分前后的代码
init(p) = l_n
final(p) = {l_x}
blocks(p) = {is^l_n,end^l_x} ∪ blocks(S)
labels(p) = {l_n,l_x} ∪ labels(S)
flow(p) = {(l_n,init(S))} ∪ flow(S) ∪ {(l,l_x) | l ∈ final(S) }
一个例子 An Example
可以将fib理解为函数，传入的变量是z，u输出的变量是v。call调用fib，传入x，0。进入if-else，如果z<3输出y=0+1，否则调用fib并且分别传入z-1,u和z-2,v进行递归算法
结构上的操作语义 Structural Operational Semantics
同样的我们要运用结构归纳法描述任意大小结构的代码实现完整分析代码。
此时的操作语义不再区分是布尔型还是整型语句，在过程间分析中，我们可以理解为只有依旧会调用函数的函数和不再调用函数的函数，与前文的<S,σ> -> σ' and <S,σ> -> <S',σ'>类似，我们依旧使用特殊字符表示，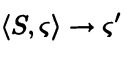
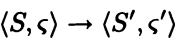
同时相较于之前简单的if语句和while语句，过程间分析的代码之间的跳转更加复杂，我们选择遍历所有有效路径的方法来记录可能出现的情况。
我们将完整的路径用CP表示：
当该语句是结束语句，即end或者出口语句，CP_l,l = l
当语句是调用函数语句，CP_l_c,CP_l = l_c,CP_l_n,l_x,CPl_r,l
当语句处在没有调用函数的流中，CP_l_1,l_3 = l_1,CP_l_2,l_3
对于可能的有效路径的标签对必须满足上述三个式子
以上面的例子为例：
CP_9,_10 = 9,CP_1,\_8,CP\_10,\_10
CP_1,_8 = 1,CP_2,\_8
CP_2,\_8 = 2,CP_3,_8 / CP2,\_4,\_8
CP\_3,_8 = 3,CP\_8,\_8
CP_4,\_8 = 4,CP\_1,_8,CP\_5,\_8
CP\_5,\_8 = 5,CP\_6,\_8
CP_6,\_8 = 6,CP\_1,\_8,CP\_7,\_8
CP_7,\_8 = 7,CP_8,\_8
CP\_8,\_8 = 8
CP\_10,\_10 = 10
执行4后一定执行5，否则就是无效路径
上下文敏感和上下文不敏感 Context-sensitive Versus Context-insensitive
为了将上下文连接在一起，对于每一次调用我们都可以看作新的数据流分析，和函数调用时的情况相似，主函数先停止运行，等待调用的函数响应。我们将主函数停止时状态表示为^l，调用的函数流起始状态表示为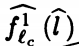
函数退出时状态表示为^l' ,主函数重新开始的状态表示为
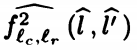。我们可以很清楚的知道主函数停止时状态等于调用函数起始状态，函数退出状态等于主函数重新开始的状态。
l和l‘的作用就是区分不同时候调用同一个函数，即记录上下文信息。
我们可以简单记录最后一次调用 ^(空) [9] [4] [6] 来判断路径是否满足有效路径，也可以记录最后两次调用 ^ [9] [9,4] [9,6] [4,4] [4,6] [6,4] [6,6] 显然记录越多的调用次数能够更加精准判断有效路径，但随着记录的增加，算法和成本会增加，所以选择合适记录数方法是最佳选择。
当然，我们也可以选择不记录：无论是何时调用，我们只在意结果的变化，不在意是哪一句调用的，回到哪一句。我们可以将语句描述为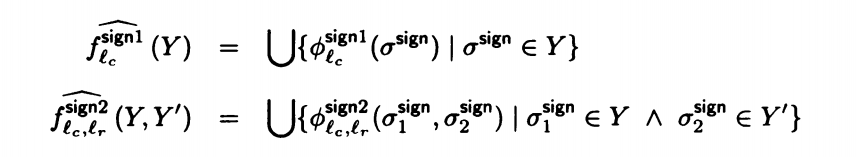
Y是所有可能的结果值。这就是上下文不敏感。
当我们选择记录时，描述就会变成：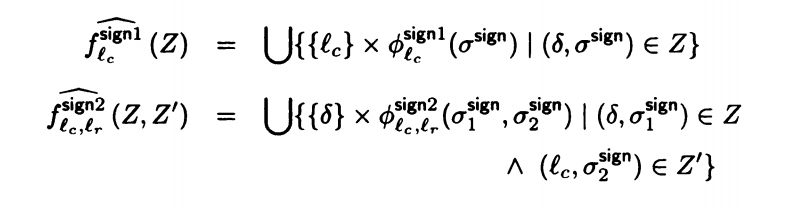
除了上面的记录调用函数的方法，我们还可以记录声明的代码语句实现上下文敏感。可以认为将每一个函数抽象为一个状态，每一次调用都对应其状态。
相对应的，我们将上下文信息依旧用δ表示，对于当前调用的抽象状态用d表示。
我们列出下面的表达式
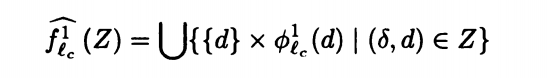
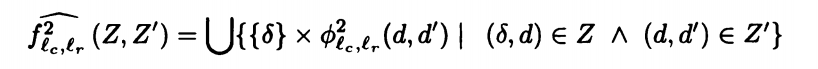
对于调用前的状态，记录在d中。对于调用的函数进行进一步划分，直到不再调用函数，将结果计算记录到d
流敏感和流不敏感 Flow-sensitive versus Flow-insensitive
至今为止，我们所讨论的数据流分析都是流敏感的分析方法，都是有时候代码的顺序不影响代码执行的结果，虽然流不敏感的分析方法可能会使结果的可能集合比流敏感的集合大（流不敏感的分析方法准确性要低于流敏感）。但是对于复杂的流敏感分析方法，流不敏感确实可以简化分析过程。
回到最初的定义，我们用流不敏感的方法描述过程间分析：
对于每一句代码执行的结果，我们可以引入AV(S)来表示
AV([skip]^l) = 空
AV([x:=a]^l) = {x}
AV(S1;S2) = AV(S_1) ∪ AV(S_2)
AV(if [b]^l then S1 else S2) = AV(S_1) ∪ AV(S_2)
AV(while [b]^l do S) =AV(S)
AV(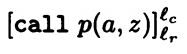) = {z}
除此之外，我们还要描述路径，用上文的CP我们可以描述成：
CP([skip]^l) = 空
CP([x:=a]^l) = 空
CP(S1;S2) = CP(S_1) ∪ CP(S_2)
CP(if [b]^l then S1 else S2) = CP(S_1) ∪ CP(S_2)
CP(while [b]^l do S) =CP(S)
CP(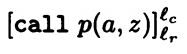) = {p}
AV(S)和CP(S)可以构成全部变量集（全局变量和局部变量），我们用IAV(S)表示
IAV(p) = (AV(S) \ {x} ) ∪ {IAV(p') |p' ∈ CP(S)}
我们可以发现，上面的定义是上下文不敏感的，每一次调用S 都是同一个S 不会有任何分别。
进一步的，我们对
进行分析
IAV(fib) = (空 \ {z} ) ∪ IAV(fib) ∪ IAV(add)
IAV(add) = {(y,u) } \ {u}
合并后可得 IAV(fib) = IAV(add) = {y}
上述分析中并没有考虑fib 和add 哪一个先定义，哪一个先调用，只是对fib和add执行的最终结果进行分析，这就是流不敏感。
指针表达式 Pointer expression
上面可以看作是对于函数的分析，接下来讲对于指针的分析。
相对于之前的AExp算法表达式，我们用PExp来表示指针表达式。相对于之前直接使用变量，我们用Sel选择器选择指针间接使用变量。其中car表示当前位置，cdr表示下一位置。
总的而言，我们可以简单描述几种表达式的状态：
a ::= p |n |a_1 op_a a_2 |nil
b ::= true | false |not b|b_1 op_b b_2 | a_1 op_r a_2 |op_p p
S ::= [p:=a]^l |[skip]^l |S_1;S_2 | if [b]^l then S_1 else S_2 |while [b]^l do S | [malloc p]^l
除此之外，我们用 ζ 来表示指针在堆中的位置，用◇表示指向空的指针。
对于指针表达式的描述，除了指针外还有表达式。和之前的描述方法相似，都是使用State
对于AExp 我们可以简单描述为fin(Z+Loc+{◇})
BExp 则为fin T
对于AExp中的变量，我们定义为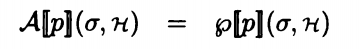
其中 σ 是指 p 的类型，在包含指针的代码中，变量不一定是类似于浮点数，整数这样的数据类型，还有可能是指针的地址，当然也有可能是空。
H 是 p 所在的heap，在包含指针的代码中，我们需要知道指针要指向的位置，为了同意描述，我们将栈顶记录，根据偏移量描述位置
对于常数，我们定义为
对于计算我们将其分解为两个变量或者常数的表达式的运算操作：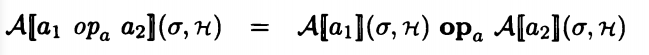
对于空指针的变量赋值为◇
相似的对于布尔类型的表达式，先描述变量再操作，描述变量的方法和运算表达式一样，操作符op_r二元运算 ，op_p单元运算。
我们用一个例子来理解一下（x指向链表的第一个位置）
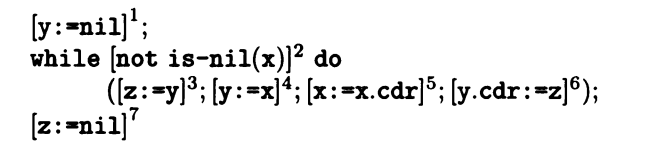
我们可以很轻松的知道这段代码的意思是，把x的链表复制到y上，而z是中间变量。
我们可以描述成：
第一句是statement声明<σ[y -> A[nil] (σ,Н)],Н>
第二句是布尔类型的语句，not (φ\is-nil(x))
第三句到第六句都是赋值语句
第七句也是声明语句<σ[z -> A[nil] (σ,Н)],Н>
其中，对于每一个形如A\z的式子都可以转换成φ\z又可以进一步改写成σ(z)
特别的形如A\y.cdr的式子先改写成φ\z.cdr再改写成H(σ(x),cdr) 当H(σ(x),cdr)指向空时，可以写成undef
由于堆是可以扩展的，在我们记录堆中数据的时候，会出现要在中间插入数据，面对这一情况，显然是十分繁琐的事情。因此我们提出抽象堆的概念，也就是相当于C++中的node，本身是独立的，通过记录前后的node位置连接整个结构。在中间插入数据只需要改变插入数据前后的node的内容。
对于这种方法，我们使用S表示抽象的声明，H表示抽象的堆，is表示抽象的位置
首先是抽象位置，如何表示一个抽象位置呢。抽象位置实质上就是某个变量的位置，我们用n_X表示。n_X 是代表实际位置 σ(x) 。
抽象声明，对于同一个变量，我们应用同一个声明，所以对于声明的描述，我们只需要记录变量名和他所在的抽象位置。
对于抽象堆，要记录变量之间的关系以及当前使用的变量值在堆中的位置。所以我们记录相关变量所在抽象位置，以及偏移量
我们用上面的例子应用一下
y = nil : 原本y指向一个抽象位置n_Y ，前后分别对应n_V n_W，执行完y = nil后，我们删掉抽象位置n_Y，创建一个n_Φ，将n_V指向n\_Φ,n\_Φ指向n\_W。
is-nil不改变
形如z = y 的式子：直接将z指向y所指向的n_Y，将n_Y变成n_Y和n_Z共同的抽象位置，同时，将z原来指向的抽象位置去除掉和z的联系
特殊的 z = y.cdr ：相类似的将z原来指向的抽象位置去除掉和z的联系，将z指向n_Y的后面一个抽象位置，并且加上z的印记
除了上面代码出现的情况，还有x = a ：把原来 x 所指向的抽象位置去除x的印记，新建一个抽象位置，加上 x 的印记。
