以语法为导向的上下文不敏感的控制流分析 Syntax Directed 0-CFA Analysis
经过上一篇的理论证明,我们得到控制流分析存在一个最小的解,但是仅仅根据上一篇文章的分析方法,我们不能利用数学的等式计算出最小解。所以我们以语法为导向得到有限约束集。使得最小解可以计算得到。
对于两个控制流分析的解,如果任意一个的最小解是另一个解的解,那么两解的公共部分一定是包含于真正的最小解之中。
例子 Example

和之前上下文不敏感的控制流分析的抽象化一样,对于let in 结构,我们可以列出这样的式子:(C , p) |= (fun f x => (f ^1(fn y => y ^2) ^3) ^4) ^5 (C , p) |= (g ^6(fn z => z ^7) ^8) ^9 C(5) 包含于 p(g) C(9) 包含于C(10)
对于fun结构,我们列出:{fun f x => (f ^1(fn y => y ^2)^3)^4}包含于C(5) 也包含于p(f) (C , p) |= (f ^1(fn y => y ^2)^3)^4
对于t_1 t_2的结构得到 (C , p) |= f ^1 (C , p) |=(fn y => y ^2)^3。
对于fn 得到{fn y => y ^2}包含于C(3) (C , p) |=y ^2
对于y ^2得到p(y) 包含于 C(2)
对于(C , p) |= (g ^6 (fn z => z ^7) ^8) ^9得到 (C , p) |= g ^6 (C , p) |= (fn z => z ^7) ^8
g为f的结果
{fn z => z ^7} 包含于 C(8) p(z) 包含于C(7)
我们可以最终得到
(C , p) |= (fun f x => (f ^1(fn y => y ^2) ^3) ^4) ^5
(C , p) |= (g ^6(fn z => z ^7) ^8) ^9
(C , p) |= (f ^1(fn y => y ^2)^3)^4
(C , p) |= f ^1
(C , p) |=(fn y => y ^2)^3
(C , p) |=y ^2
(C , p) |= g ^6
(C , p) |= (fn z => z ^7) ^8
上述式子我们可以合并成(C , p) |= (fun f x => (f ^1(fn y => y ^2) ^3) ^4) ^5 (C , p) |= (g ^6(fn z => z ^7) ^8) ^9。
接下来,我们简单证明上面的结果是代码的最小解:我们将整段代码的关系记作(C ^T, p ^T),也就是任意一句包含在这一段代码中的代码的关系(C , p)都包含在(C ^T, p ^T)中,同样的每一句代码的最小解也一定包含于(C ^T, p ^T)中。所以,当(C ^1, p ^1) 和(C ^2, p ^2)拥有一个共同的表达式满足对应关系,那么这个表达式就可以对(C ^1, p ^1) 和(C ^2, p ^2)进行共同描述。
根据上面的定理我们可以得到上述的结果是所有(C , p)的共同描述。
同时,由于(C , p)是有限的,(C , p)的任何描述的子集都在上述结果中,所以上述结果是一个摩尔集,也就是最小解。
基于约束的上下文不敏感的控制流分析Constraint Based 0-CFA Analysis
在之前的分析中,我们已经实际上已经得到了控制流的约束条件。对于上述例子就是满足
C(5) 包含于 p(g)
C(9) 包含于C(10)
f 包含于C(5) 也包含于p(f)
{fn y => y ^2}包含于C(3)
p(y) 包含于 C(2)
p(z) 包含于C(7)
也就是说控制流的约束条件就是满足(C , p) |= e_0的条件
即:(我们将C[]表示为约束条件)
C[c ^l] = 空集
C[x ^l] = {r(x) 包含于 C(l)}
C[(fn x => e_0) ^l] = {{fn x => e_0} 包含于 C(l)} C(e_0)
C[(fun f x => e_0) ^l] = {{fun f x => e_0} 包含于 C(l)} C(e_0) {{fun f x => e_0} 包含于 r(f)}
C[(t_1 ^l_1 t_2 ^l_2) ^l] = C[t_1 ^l_1] C[t_2 ^l_2] 当fn x => t_0 ^l_0在t_1中或者 fun f x => t_0 ^l_0在t_1中 时 C(l_2) 包含于 r(x) C(l_0) 包含于 C(l)
C[(if t_0 ^l_0 then t_1 ^l_1 else t_2 ^l_2) ^l] = C[t_0 ^l_0] C[t_1 ^l_1] C[t_2 ^l_2] C[l_1] 包含于 C[l] C[l_2] 包含于 C[l]
C[(let x = t_1 ^l_1 in t_2 ^l_2) ^l] = C[t_1 ^l_1] C[t_2 ^l_2] C[l_1] 包含于 r[x] C[l_2] 包含于 C[l]
C[(t_1 ^l_1 op t_2 ^l_2) ^l] = C[t_1 ^l_1] C[t_2 ^l_2]
例子Example
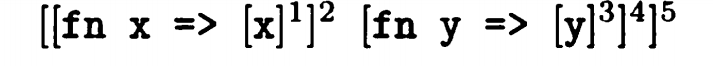
C[((fn x = x ^1) ^2 (fn y => y ^3) ^4) ^5] = {
{fn x => x ^1} 包含于 C(2)
r(x) 包含于 C(1)
{fn y => y ^3} 包含于 C(4)
r(y) 包含于C(3)
左表达式包含参数,右表达式对左表达式的参数进行操作 ==> C(4) 包含于 r(x)
C(4)对y进行操作 ==> C(4) 包含于 r(y)
C(1) 包含于 C(5)
C(3) 包含于 C(5)
}
C[e_0] 和 (C , p)关系是C[e_0]是约束关系的实体,(C , p)是约束关系的逻辑表示,(C , p) |= e_0 需要满足 C[e_0] 。约束条件中的C(l) 与 (C , p)的C对应 。r(x) 与 (C , p)中的p对应。
我们对于相互转化的关系用 (C , p) [C(l)] = C(l) 和 (C , p)[r(x)] = p(x)表示。
其中对于基本类型语句t (C , p) [{t}] = {t} 对于本身是运算又会返回值参与其他运算的语句t (C , p) [{t}] 包含于 rhs' => lhs] = (C , p) [lhs]
所以我们可以得到这样的式子 (C , p) |= C[e]
我们简单证明式子成立且为最小解: 举一个t_1 ^l_1 t_2 ^l_2的例子,l_1的运算结果会运用到t_2中所以(C_1, p_1)包含于(C_2, p_2),也就是约束条件渐渐叠加。因为(C ,p) 是有限个,所以有一个解是极限值,也就是最小解。
在实际应用中,我们可以用链表的形式记录:
对一个C[e]的约束条件,我们生成(C , p)来储存。首先进行初始化,生成空的链表,然后根据语句类型生成限制条件链以及变量,当语句为fn x => x 时将id_x保存至D[C(l)]中并且生成限制条件添加在E[q]中。当语句是其他时,生成限制条件添加在E[q]中。然后根据约束条件生成由最初的根语句对应的工作列表的解逐步演变成最终工作列表的解。即将参数id根据约束条件记录进D[C(l)]中。
我们简单证明该解为最小解:首先,对于第一步和第二步是显然有界的,第三部由于代码块有限,所以约束条件也是有终止的。所以解是可计算的。然后证明为最小解,假设(C‘ , p’) |= C[e] 那么任意D[C(l)] 包含于 C'(l)中 D[r(x)] 包含于 p'(x)中。这在第一步中实现。随后第二部中保证了对于任何形式的t p的处理使得(C , p) |= C[e]始终满足。所以该解为最小解。
根据上面的描述,我们得到以下结论:(C , p) |= C[e] 是最小解,以语法为导向和基于约束的结果是相同的,
伪代码
Init : W = nil D[q] = nil E[q] = nil
Build :
for cc in C[e] :
case cc of
{t} p : add(p,{t})
p1 p2 : E[p1] = cons(cc,E[p1])
t p => p1 p2:E[p1] = cons(cc,E[p1]) E[p] = cons(cc,E[p])
Iteration :
while W ≠ nil :
q = head(W) W = tail(W)
for cc in E[q]
case cc of
p1 p2 : add(p2,D[p1])
{t} p => p1 p2: if t ∈ D[p] then add(p2,D[p1])
添加数据流分析 Adding Data Flow Analysis
控制流分析可以通过添加数据流分析的内容使得控制流分析对于变量的分析不再仅仅是抽象表示,也会包含抽象值。
首先我们要对控制流分析本身的val进行拓展,使得它满足数据流分析的要求:将bool类型和int类型的值进行抽象表示,其中包括tt为True ff为False -为负数 0为0 +为正数。同时我们定义运算 - 和 - 运算依旧是 -。 - 和 0 运算依旧是-。 -和+运算可能是 - 0 + 。0和0运算是0.+和+运算是+。
由于对于val进行了拓展,所以对于(C , p) |= c ^l需要将d_c记录到C(l)中从而实现数据流分析。
例子 Example

这是一个包含常数的let in语句
(C , p) |= (let f = () ^9 in () ^14) ^15可以得到约束条件C(9) 包含于 p(f) C(14) 包含于C(15)以及(C , p) |= () ^9 (C , p) |= () ^14
(C , p) |= (fn x => () ^8) ^9可以得到 {fn x => () ^8} 包含于 C(9)
(C , p) |= (if (x ^1 > 0 ^2) ^3 then (fn y => y ^4) ^5 else (fn z => 25 ^6) ^7) ^8可以得到(C , p) |= (x ^1 > 0 ^2) ^3 当C(3) 为true时,(C , p) |= (fn y => y ^4) ^5 C(5)包含于C(8) 。当C(3) 为false时,(C , p) |= (fn z => 25 ^6) ^7 C(7)包含于C(8) 。
(C , p) |= (x ^1 > 0 ^2) ^3 可以得到 (C , p) |= x ^1 (C , p) |= 0 ^2 x ^1 > 0 ^2 包含于 C(3)
(C , p) |= x ^1 可以得到 p(x) 包含于C(1)
(C , p) |= 0 ^2 可以得到{d_0} 包含于 C(2)
(C , p) |= (() ^12 0 ^13) ^14 可以得到(C , p) |= () ^12 (C , p) |= 0 ^13
(C , p) |= (f ^10 3 ^11) ^12可以得到(C , p) |= f ^10 (C , p) |= 3^11
(C , p) |= 0 ^13可以得到{d_0} 包含于 C(13)
(C , p) |= f ^10可以得到p(f) 包含于C(10)
(C , p) |= 3^11可以得到{d_3} 包含于C(11)
约束条件:
C(9) 包含于 p(f)
C(14) 包含于C(15)
{fn x => () ^8} 包含于 C(9)
当C(3) 为true时,(C , p) |= (fn y => y ^4) ^5 C(5)包含于C(8) 。
当C(3) 为false时,(C , p) |= (fn z => 25 ^6) ^7 C(7)包含于C(8) 。
{x ^1 > 0 ^2} 包含于 C(3)
p(x) 包含于C(1)
{d_0} 包含于 C(2)
{d_0} 包含于 C(13)
p(f) 包含于C(10)
{d_3} 包含于C(11)
由于x ^1的实参是3 ^13。所以{+}包含于C(1)。由于C(2)为{0},所以C(3)为{tt}。约束条件为(C , p) |= (fn y => y ^4) ^5 C(5)包含于C(8)
(C , p) |= (fn y => y ^4) ^5得到 {fn y => y ^4} 包含于 C(5)
最终,我们得到
(C , p)(C(1)) = {+}
(C , p)(C(2)) = {0}
(C , p)(C(3)) = {tt}
(C , p)(C(4)) = {+}
(C , p)(C(5)) = {fn y => y ^4}
(C , p)(C(6)) = {}
(C , p)(C(7)) = {}
(C , p)(C(8)) = {fn y => y ^4}
(C , p)(C(9)) = {fn x => () ^8}
(C , p)(C(10)) = {fn x => () ^8}
(C , p)(C(11)) = {+}
(C , p)(C(12)) = {fn y => y ^4}
(C , p)(C(13)) = {}
(C , p)(C(14)) = {}
(C , p)(C(15)) = {}
(C , p)(p(f)) = {fn x => () ^8}
(C , p)(p(x)) = {+}
(C , p)(p(y)) = {0}
(C , p)(p(z)) = {}
相较于单纯的控制流分析,改变的是减少了对于不执行的代码的约束条件的分析,增加了对变量的描述。
即单纯的控制流分析是
(C , p)(C(1)) = {}
(C , p)(C(2)) = {}
(C , p)(C(3)) = {}
(C , p)(C(4)) = {}
(C , p)(C(5)) = {fn y => y ^4}
(C , p)(C(6)) = {}
(C , p)(C(7)) = {fn z => 25 ^6}
(C , p)(C(8)) = {fn y => y ^4 ,fn z => 25 ^6}
(C , p)(C(9)) = {fn x => () ^8}
(C , p)(C(10)) = {fn x => () ^8}
(C , p)(C(11)) = {}
(C , p)(C(12)) = {fn y => y ^4 ,fn z => 25 ^6}
(C , p)(C(13)) = {}
(C , p)(C(14)) = {}
(C , p)(C(15)) = {}
(C , p)(p(f)) = {fn x => () ^8}
(C , p)(p(x)) = {}
(C , p)(p(y)) = {}
(C , p)(p(z)) = {}
添加上下文敏感 Adding Context Information
依旧是根据实例介绍内容
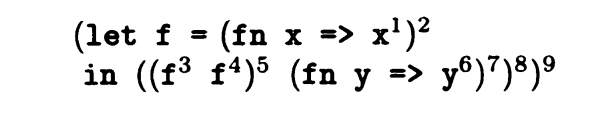
let in结构 C(2) 包含于 p(f) C(8) 包含于 C(9)
fn x => x ^1 结构 {fn x => x ^1} 包含于 C(2)
f ^3 f ^4 结构 C(4)包含于p(x) C(1)包含于C(5)
fn y => y ^6 结构 {fn y => y ^6}包含于 C(7)
() ^5 () ^7 结构 C(7) C(5)包含于 p(x) C(1)包含于C(8)
x ^1 结构 p(x) 包含于 C(1) p(y) 包含于 C(6)
包含链:
{fn x => x ^1} 包含于 C(2) 包含于 p(f)
{fn y => y ^6}包含于 C(7) 包含于 p(x)
C(1) 包含于 C(8) 包含于 C(9)
C(1)包含于C(5)包含于 p(x) 包含于 C(1)
p(y) 包含于 C(6) 包含于 C(7) 包含于 p(x)
(C , p)结果:
C(1) = {fn x => x ^1 , fn y => y ^6}
C(2) = {fn x => x ^1}
C(3) = {fn x => x ^1}
C(4) = {fn x => x ^1}
C(5) = {fn x => x ^1 , fn y => y ^6}
C(6) = {fn y => y ^6}
C(7) = {fn y => y ^6}
C(8) = {fn x => x ^1 , fn y => y ^6}
C(9) = {fn x => x ^1 , fn y => y ^6}
p(f) = {fn x => x ^1}
p(x) = {fn x => x ^1 , fn y => y ^6}
p(y) = { fn y => y ^6}
这一过程就是上一篇文章的最后伪代码部分做的工作
对于单一let in结构的代码,我们之前的描述就足够了,并且不会特别复杂,但是面对多重let in结构,就会出现描述冗余复杂的情况。比如:

仅仅使用上面的描述,我们得到
(fn x1 => x1) 包含于 p(f1)
(let f1 in) 包含于 C(let in let in)
fn x2 =>x2 包含于 p(f2)
((f1 f2) fn y => y) 包含于 C(let in)
fn y => y 包含于 C()
也就是最小解是(fn x1 => x1) fn x2 =>x2 fn y => y
这说明随着let in结构的增加,最小解的集合会变大,其中的冗余会变多。冗余所在就是,对于x1来说只和fn x2 => x2发生关系 ,x2只和 fn y => y 发生关系。也就是我们可以只是用fn y => y来描述这个程序。
所以我们提出上下文敏感来实现变量的溯源。
上下文敏感的控制流分析 k-CFA Analysis
上下文敏感就是找到不同调用点各参数之间的关系,也就是将虚参对应的实参找到并且记录。
当语句是x ^l 时,我们记录x为p(x,ce(x))保存在C(l,δ)中
p(x,ce(x))表示当前虚参为x,在上下文环境变量中找到该虚参对应的实参,或者先找到对应实参一致的虚参。
当语句是fn x => e_0时,我们记录为(fn x => e_0,ce_0) 保存在C(l,δ)中。
(fn x => e_0,ce_0)表示当前虚参为fn x => e_0,以及上下文环境中的实参。
其他的语句描述类似,相较于上下文不敏感的控制流分析多了上下文环境变量的记录和语句所对应的上下文环境变量的集合。
除此之外,上下文敏感的控制流分析多了一些条件:即对于fn x=> x来说ce_0是最终的环境变量集合。fun也是一样。对于t_1 t2的结构,则存在当前执行环境为一个环境变量集合。将环境变量和语句标签记录在一起,记作δ_0。并将当前语句变量和这个集合建立对应关系当作新的环境变量,记作ce_0[x -> δ\_0]
例子 Example
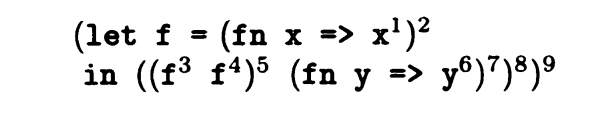
一个let in结构说明只有一次调用,也就是1-CFA
我们利用上下文敏感的控制流分析进行描述:
上述例子中 f 为调用的函数,为一个小的分析单元。我们记作ce_0[f -> ^],即在分析前,环境变量暂时没有参数。
对于in中的代码,存在 f ^3 f ^4和() ^5 () ^7 的结构,也就是存在两个小的环境变量集合,记作ce_0[x -> 5] ce_0[x -> 8]
由于 f 在执行5时进行转化,所以对于 f 的分析要包括C(5)的环境变量,同理由于() ^8为最外面的语句,所以在调用 f 时,也需要C(8)的环境变量,我们可以得到:
C(1,5) = {(fn x => x ^1 ,ce_0)}
C(1,8) = {(fn y => y ^6 ,ce_0)}
C(2,^) = {(fn x => x ^1 ,ce_0)}
C(3,^) = {(fn y => y ^6 ,ce_0)}
C(4,^) = {(fn x => x ^1 ,ce_0)}
C(5,^) = {(fn y => y ^6 ,ce_0)}
C(7,^) = {(fn x => x ^1 ,ce_0)}
C(8,^) = {(fn y => y ^6 ,ce_0)}
C(9,^) = {(fn x => x ^1 ,ce_0)}
p(f,^) = {(fn x => x ^1 ,ce_0)}
p(x,5) = {(fn x => x ^1 ,ce_0)}
p(x,8) = {(fn y => y ^6 ,ce_0)}
笛卡尔积算法CPA The Cartesian Product Algorithm
我们使用笛卡尔积算法来实现控制流分析。
首先笛卡尔积算法是什么:循环内下沉到最小单元再进行新的循环。也就是我们之前的分析过程,先分析let in结构,再分析let中的内容,直到let分析到最小单元,分析in重复操作。
由于控制流分析是将程序代码从整体到局部的按步分析的方法,同时控制流分析并不需要将每一次分析的结果进行整合化简,所以笛卡尔积算法很适合控制流分析。
总结
控制流分析适用于以函数为导向语言,即对于每一部分函数都是一个单元,存在自身的环境变量,对于一个程序,我们先对所有函数进行分析,再在主函数中将这些环境变量应用实现对程序的分析。
当然控制流分析也适用于以对象为导向的语言,每一个对象都是一个单元,存在自身环境变量,对于一个程序,我们先对对象进行分析,再在代码中应用这些分析结果,即环境变量。
控制流分析是基于约束的分析的一种,我们首先进行抽象表示,并对约束条件进行分析,然后利用代码处理程序使得生成约束条件,最后找到最终解。




