首页

阅读

活动

安全导航

内容精选

首发于

LuoXuan

程序分析理论初实践初探索

DR003XM

所谓归属感

re2c

前言

本文主要依据NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions Ville Laurikari Helsinki University of Technology Laboratory of Computer Science PL 9700, 02015 TKK, Finland vl@iki.fi这篇论文以及re2c自身代码进行描述。

EXP抽象化

re2c的抽象化过程和我们程序分析理论中的内容有很高的一致性。首先是最基本的结构单元EXP。每一句代码都是EXP，而这些EXP往往可以进一步分解：如123+234，在程序分析理论的结构上的操作语义部分，我们提出了这样的分析方法：A[a1 opa a2]σ = A[a1]σ opa A[a2]σ。这里也是一样，同时还增加了实际分析的细节：首先，我们将123+234整个EXP转换成EXP+EXP。随后对第一个EXP进行同样的分解。由于123不包含op所以转换成VAR。对于VAR我们进行按位读取识别：将第一位和后续分开。第一位看作DGT，后续看作新的VAR。直到将123全部识别。随后对234进行同样的操作。

即

EXP->EXP+EXP->VAR+EXP->1 VAR +EXP ->12 VAR +EXP ->123+EXP->123+VAR->123+2 VAR->123+23 VAR ->123+234

NFA自动机

NFA Nondeterministic Finite Automaton 非确定有限状态自动机

有限状态自动机。首先对状态进行定义，状态是自动机每一次处理信号的结果，每一次接收信号后会进入新的状态，这个状态可能是循环状态（处理信号后之前的处理机制依旧适用），也可能是下一个状态（已经不适用于相同状态的处理，需要进入新的状态，应用新的处理机制）

要实现上面所描述的状态，需要进行相应的运算，对于应用新的处理机制的运算为组合运算，用RS表示。对于依旧使用当前机制的运算为重复运算，用R^*表示。除此之外，还有替换运算：从当前状态转换到下一状态可以应用两种不同的处理机制，比如说一个EXP可以处理成VAR，也可能是一个函数的调用。用R|S表示。

DFA自动机

DFA Deterministic Finite Automaton 确定有限状态自动机

其确定性在于该模型用于解决已知字符串是否满足自动机设置。即满足条件就继续否则退出，这种是就是是不是就是不是的设置使得自动机只存在一条路径，不会出现R|S的运算。这不代表DFA自动机一次只能应用一种处理机制，DFA自动机和NFA自动机实际可以相互转化，DFA自动机每一个状态的处理机制是NFA相对应处理机制的集合。

即对于下面一个NFA自动机，我们可以转换成如图二所示的DFA自动机

图一

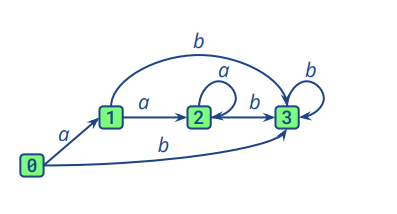
图二

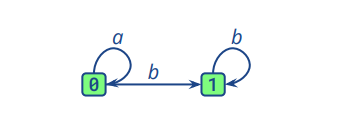
图二中的0包含图一中的0,1,2：在接收初始状态时，进入NFA的0，也就是DFA中的0(0)。接收到a则进入NFA的1，也就是DFA中的0(1)。接收到b则直接进入NFA的3，也就是DFA的1(3)。其余部分相似。所以DFA的处理机制是NFA处理机制的集合。

TNFA自动机

NFA with tagged transitions就是在NFA的基础上加上了tag元素，用于记录自动机处理过程。

也就是TNFA不仅包含NFA中有的有限个状态，有限个符号，运算关系，初始状态，结束状态，还包含有限个标签。

在处理一个输入时，首先接收前，自动机处于上一个状态，接收输入时，设置tag在当前处理机制，进入下一个状态

虽然加上了Tag，但是NFA的不确定性依旧存在，所以我们要把TNFA转换成DA deterministic automata。

首先，我们要找到初始状态，根据TNFA的处理机制确定TDFA的初始状态。再根据所有的处理机制，将处理机制进行分类集合，形成TDFA的处理机制。最后确定退出状态。

TDFA自动机

同样的TDFA是加上了tag的DFA。

相较于TNFA，TDFA不仅包含有限个状态，有限个符号，初始状态，最终状态，还包含过度函数，初始化和终止化。

tag的作用

当我们想要匹配[0-9]*[a-z]\*的时候，在[0-9]和[a-z]之间的处理机制的转换在没有tag的时候不能明确标识出来。加入tag后，我们不再需要通过检测到非[0-9]切换处理机制，再重复读取该非[0-9]的信号。

当然，tag的添加不具有唯一性，比如正则表达式为(a|b)*t_0 b (a|b)\*的处理机制，对于abba信号，t_0可以标记在第一个a后面，也可以标记在第一个b后面。为此，我们添加一项原则使得tag唯一。对于包含重复处理机制的匹配，我们尽可能的多去实现重复，也就是说，除非当前处理机制不能应用，或者应用当前匹配机制后无法继续匹配，否则使用当前处理机制。

例子

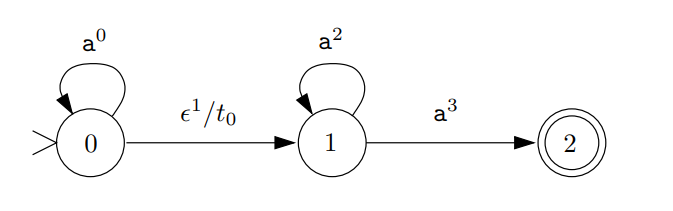
0是初始状态，接收信号后，可能应用同样的处理机制或者进入下一状态。所以TDFA的初始状态也是0.

状态1可能使用同样的处理机制也可能进入状态2，而状态2是TNFA的终止状态，所以对于TNFA的1，2是TDFA的1，也是TDFA的终止状态。除此之外，TDFA具有终止化操作，即对于进入TDFA的1(2)后，会退出程序。同样的，在TDFA的初始状态0中，会包含初始化达到使用新的处理机制进入程序的作用。其中，过度函数就是应用处理机制时记录标签从而达到记录执行过程的作用。

伪代码实现

对于一个状态t，进行a处理

对于任意状态u->u'之间存在a处理，则添加到链表中。

reach(t,a)

for u->u' == a ： r = r + (u' , k)

当前状态所有可能的处理机制进行遍历，找到进入其他状态的最短路径。

t_closure

for (u , k) ∈ S (：push(u,0,k) ;)

init closure

while stack (: pop(s,p,k) ; for s -> u (: if tag (: remove ; add )

if (u,p',k') ∈ closure and p < p' (: remove (u,p',k') ;) if (u,p.k) not ∈

closure : (add(u,p,k) ; push (u,p,k))))

将TNFA转换成TDFA

for map item : add map item to init ; signal map item

while signal map item : unsignal signal item ; for symbol : u <- t_closure(reach(t,a)) ; c <- list ;for map item in u : if map item not in k : add map item to c ; if u -> u' == R : add R to c ; else signal u' ; t = u' ; c = a ; if u' == final : finish ;

伪代码执行流程：

将当前状态的处理机制保存到链表中，将所有保持0状态的处理机制添加到初始化部分。接收信号，将所有能够处理a信号的处理机制添加到新的链表中，并且将该链表中的处理机制进行筛选，找到能够跳转的最短的应用链群。将跳转的状态和使用的处理机制链记录，重复上述步骤处理新的状态直到进入终止状态。

popmaster

看到作者的出题思路是抽象代码树和污点分析，因为之前发了几篇程序分析理论的文章但是一直没有实践，所以拿这道题自己实践一下。

污点分析在第一篇程序设计分析理论中，我写的是语义分析，但在后面的文章中还没有正式出现。关于抽象代码树，要在后面的抽象解释才提到。

我们已经介绍的只是数据流分析的部分内容，所以这篇文章首先会是根据数据流分析的过程间分析编写一个遍历以入口函数为起点的所有路径的脚本实现代码分析。

最后我们还会看一看出题人的exp，提前看看抽象解释和污点分析，为我们后面的学习建立一个预期。

编程思路

这一道题是一个单输入多输出的问题，根据之前流的理论，我们应该从输入开始分析。同时这道题是函数的跳转，所以我们选择过程间分析。根据上下文敏感的想法，我们在分支处应该是调用函数，主函数暂停，执行调用函数，调用函数退出的状态是主函数重新开始的状态。基于这一理论，我们定义一个函数，当出现分支时继续调用自身函数，未出现分支时，如果依旧是过程函数，还是调用自身，如果是eval输出函数，那么结束并输出pop链

除此之外，不少师傅在比赛时，选择从eval开始判断，先寻找不覆盖变量的eval，再往上找。是使用了逆流分析的方法，在之前的文章里，我们提到逆流分析一般是多输入单输出的情况，为什么这里单输入多输出会使用逆流分析呢，主要是只需要找到一条链，多输出转换成了单输出，把这道题变成了单输入单输出的问题。当然，这并不意味着多输出的程序不能用逆流分析的方法。只是缺少了一些过程间分析的内容。

编写过程

类，函数，变量

函数有过程的函数和结束的eval函数

变量就是每一次要赋值的类名

这一个程序主要是跳转比较多，每一个具体执行没有太多需要注意的安全问题，要结合过程间分析编写代码。

我们之前提到过程间分析需要记录跳转前跳转后状态。在这里主要是记录上一个类和下一个类是哪个的问题。这个时候想到树结构能够记录上下同时满足多个分支。

在众多树结构中，我们想到结构归纳法帮助我们简化逻辑，在这个程序中最小单元是函数，我们用函数当作树状图的元素。我们记录每一个函数属于哪个类便于变量赋值，把函数是eval的当作终点。

对于一个形如

class Un9h32{
    public $msePmc1;
    public function NndvxI($HeqXE){
        for($i = 0; $i < 35; $i ++){
            $aKMhTe= $HeqXE;
        }
        if(method_exists($this->msePmc1, \'T0bEwD\')) $this->msePmc1->T0bEwD($HeqXE);
        if(method_exists($this->msePmc1, \'CdFIxA\')) $this->msePmc1->CdFIxA($HeqXE);

}
public function gQLRqZ($cMmLT){
    eval($cMmLT);

}

}

的类，我们需要记录类名，函数，函数指向的函数/eval

我们要让python读取class后面的内容直到{ 记录为类名

public $直到 ; 记录为变量名

public function 直到 ( 记录为函数名

$this->xxx-> 直到( 记录为下一个函数名

封装成一个以函数名为主键的表，

先是一个类的封装

因为不会字符匹配所以仅仅通过位置获取，通用性差，后面再修改

代码如下

#coding=utf-8
import os, sys, re

i = 1
j = 1

class func:
    class_name = \'\'      #类名
    cur_function = \'\'     #当前函数名
    next_function = []    #下一个函数名
    var = \'\'         #变量名
    bool_cur = False     #是否是eval
    bool_next = False   #下一个函数是否多个    

    

with open(\'asd.php\') as file:
    for content in file:
        if \'class\' in content:
            class_name = content[6:12]
        if \'public $\' in content:
            var_name = content[12:19]
        if \'public function\' in content:
            f = func()
            f.cur_function = content[20:26]
            f.class_name = class_name
            f.var = var_name 
            i = i + 1
            j = 1
        if \'eval\' in content:
            f.bool_cur = True
        if \'method_exists\' in content:
            f.next_function.append(content[62:68])
            if j>1 :
                f.bool_next = True
            j = j + 1
print(f.class_name)
print(f.cur_function)
print(f.var)
print(f.bool_next)
print(f.bool_cur)
print(f.next_function[1])

拓展到多个类

由于树状结构本人不会，所以用写一个文件的方式构造树结构

#coding=utf-8
import os, sys, re

i = 1
j = 1
m = 1


class func:
    class_name = \'\'      #类名
    cur_function = \'\'     #当前函数名
    next_function = []    #下一个函数名
    var = \'\'         #变量名
    bool_cur = False     #是否是eval
    bool_next = False   #下一个函数是否多个



w_file=open(\'tree.txt\',\'w\')

#读取记录    

with open(\'asd.php\') as file:
    for content in file:
        if \'class\' in content:
            class_name = content[6:12]
        if \'public $\' in content:
            var_name = content[12:19]
        if \'public function\' in content:
            if i > 1 :
                w_file.write(f.cur_function)
                w_file.write(\'\\n    class_name \')
                w_file.write(f.class_name)
                while j > m:
                    w_file.write(\'\\n      f \')
                    w_file.write(f.next_function[m-1])
                    m = m + 1

            w_file.write(\'\\n    var \')    
            w_file.write(f.var)
            w_file.write(\'\\n    bool_cur \')
            w_file.write(str(f.bool_cur))
            w_file.write(\'\\n    bool_next \')
            w_file.write(str(f.bool_next))
            w_file.write(\'\\n\')


            
            f = func()
            f.cur_function = content[20:26]
            f.class_name = class_name
            f.var = var_name 
            i = i + 1
            

    if \'eval\' in content:
        f.bool_cur = True
    if \'method_exists\' in content:
        f.next_function.append(content[62:68])
        if j>1 :
            f.bool_next = True
        j = j + 1

处理数据，使数据成为链状结构。

定义函数

#处理数据

def paixu(content,keyword):    
    pre_content = content + keyword +\'-->\'
    position = tree_content.find(keyword)
    key_position = tree_content.find(\'f \',position)
    keyword = tree_content[key_position+2:key_position+8]             
    post_next = tree_content.find(\'bool_next\',position)
    num = tree_content[post_next+10:post_next+11]
    num = int(num)
    while num >= 1:
        paixu(pre_content,keyword)
        key_position = tree_content.find(\'f \',key_position+1)
        keyword = tree_content[key_position+2:key_position+8]
        num = num - 1
    post_cur = tree_content.find(\'bool_cur\',position)
    current = tree_content[post_cur+9:post_cur+10]
    current = int(current)
    print(pre_content)
    if current == 1:
        w_file.write(pre_content+\'\\n\')
        print(pre_content+\'\\n\')

但是python递归深度有限制，同时可能会导致栈溢出

仅仅针对这一道题，我们限制链的长度，先找到一条能够到eval的链

t = 0

#处理数据

def paixu(content,keyword,t):    
    pre_content = content + keyword +\'-->\'
    if t > 10:
        print(pre_content)
        r_file.write(pre_content+\'\\n\')
        return 0

position = tree_content.find(keyword)
key_position = tree_content.find(\'f \',position)
keyword = tree_content[key_position+2:key_position+8]             
post_next = tree_content.find(\'bool_next\',position)
num = tree_content[post_next+10:post_next+11]
num = int(num)
while num >= 1:
    t = t + 1
    paixu(pre_content,keyword,t)
    key_position = tree_content.find(\'f \',key_position+1)
    keyword = tree_content[key_position+2:key_position+8]
    num = num - 1
post_cur = tree_content.find(\'bool_cur\',position)
current = tree_content[post_cur+9:post_cur+10]
current = int(current)    
if current == 1:
    print(pre_content)
    r_file.write(\'\\n\')
    r_file.write(pre_content+\'\\n\')
    r_file.write(\'\\n\')
    return 0

从入口开始找路径

#coding=utf-8
import os, sys, re

sys.setrecursionlimit(3000)

class func:
    class_name = \'\'      #类名
    cur_function = \'\'     #当前函数名
    next_function = []    #下一个函数名
    var = \'\'         #变量名
    bool_cur = 0     #是否是eval
    bool_next = 0   #下一个函数是否多个





#读取记录    
def read():
    i = 1
    j = 0
    m = 1
    k = 0
    w_file=open(\'tree.txt\',\'w\')
    with open(\'class.php\') as file:
        for content in file:
            if \'class\' in content:
                class_name = content[6:12]
            if \'public $\' in content:
                var_name = content[12:19]
            if \'public function\' in content:
                if i > 1 :
                    w_file.write(\'cur \')
                    w_file.write(f.cur_function)
                    w_file.write(\'\\n    class_name \')
                    w_file.write(f.class_name)
                    while j >= m:
                        w_file.write(\'\\n      f \')
                        w_file.write(f.next_function[m-1])
                        m = m + 1

                w_file.write(\'\\n    var \')    
                w_file.write(f.var)
                w_file.write(\'\\n    bool_cur \')
                w_file.write(str(f.bool_cur))
                w_file.write(\'\\n    bool_next \')
                w_file.write(str(f.bool_next))
                w_file.write(\'\\n\')

            k = 0
            f = func()
            f.cur_function = content[20:26]
            f.class_name = class_name
            f.var = var_name 
            i = i + 1
            
        if \'eval\' in content:
            f.bool_cur = 1
        if \'method_exists\' in content:
            f.next_function.append(content[62:68])
            j = j + 1
            k = k + 1
            f.bool_next = k
        else:
            if \'$this->\' in content:
                next_position = content.find(\'$this->\')
                true = content.find(\'->\',next_position+7)
                if true != -1:
                    f.next_function.append(content[next_position+16:next_position+22])
                    j = j + 1
                    k = k + 1
                    f.bool_next = k


t = 0

#处理数据

def paixu(content,keyword,t):    
    position = tree_content.find(\'cur \'+keyword)
    pre_content = content + keyword +\'-->\'
    post_cur = tree_content.find(\'bool_cur\',position)
    current = tree_content[post_cur+9:post_cur+10]
    current = int(current)
    if current == 1:
        print(\'yes  \'+pre_content)
        r_file.write(\'yes  \')
        r_file.write(pre_content+\'\\n\')
        r_file.write(\'\\n\')
        return 0
    if t > 30:
        print(\'no  \'+pre_content)
        r_file.write(pre_content+\'no\\n\')
        return 0

key_position = tree_content.find(\'f \',position)
keyword = tree_content[key_position+2:key_position+8]             
post_next = tree_content.find(\'bool_next\',position)
num = tree_content[post_next+10:post_next+11]
num = int(num)
while num >= 1:
    t = t + 1
    paixu(pre_content,keyword,t)
    key_position = tree_content.find(\'f \',key_position+1)
    keyword = tree_content[key_position+2:key_position+8]
    num = num - 1
    t = t - 1


    


    
content = \'\'

\\#read()

r_file=open(\'result.txt\',\'w\')
with open(\'tree.txt\') as w_file :
    keyword = \'qZ5gIM\'
    tree_content = w_file.read()
    position = tree_content.find(keyword)    
    content = keyword + \'-->\'
    key_position = tree_content.find(\'f \',position)
    keyword = tree_content[key_position+2:key_position+8]
    post_next = tree_content.find(\'bool_next\',position)
    num = tree_content[post_next+10:post_next+11]
    num = int(num)
    while num >= 1:
        t = t + 1
        paixu(content,keyword,t)
        key_position = tree_content.find(\'f \',key_position+1)
        keyword = tree_content[key_position+2:key_position+8]
        num = num - 1

验证可行

要把有覆盖变量的eval去除掉

我们将read 读取eval 的语句改成

if 'eval' in content: f.bool_cur = 1 if '=\'' in content[:-1]: f.bool_cur = -1

到这一步已经可以完成pop链查找

但是我比较好奇是不是有一条没有拼接的链

所以继续加限制

#coding=utf-8
import os, sys, re ,linecache

sys.setrecursionlimit(3000)

class func:
    class_name = \'\'      #类名
    cur_function = \'\'     #当前函数名
    next_function = []    #下一个函数名
    var = \'\'         #变量名
    bool_cur = 0     #是否是eval
    bool_next = 0   #下一个函数是否多个
    token = 0





#读取记录    
def read():
    token = \'\'
    i = 1
    j = 0
    m = 1
    k = 0
    last_last_last_content = \'\'
    last_last_content = \'\'
    last_content = \'\'
    now_content = \'\'
    w_file=open(\'tree.txt\',\'w\')
    with open(\'class.php\') as file:
        for content in file:
            last_last_last_content = last_last_content
            last_last_content = last_content
            last_content = now_content
            now_content = content
            if \'class\' in content:
                class_name = content[6:12]
            if \'public $\' in content:
                var_name = content[12:19]
            if \'public function\' in content:
                if i > 1 :
                    w_file.write(\'cur \')
                    w_file.write(f.cur_function)
                    w_file.write(\'\\n    class_name \')
                    w_file.write(f.class_name)
                    while j >= m:
                        w_file.write(\'\\n      f \')
                        w_file.write(f.next_function[m-1])
                        m = m + 1

                    w_file.write(\'\\n    var \')    
                    w_file.write(f.var)
                    w_file.write(\'\\n    bool_cur \')
                    w_file.write(str(f.bool_cur))
                    w_file.write(\'\\n    bool_next \')
                    w_file.write(str(f.bool_next))
                    w_file.write(\'\\n    token \')
                    w_file.write(str(f.token))
                    w_file.write(\'\\n\')
    
                k = 0
                f = func()    
                f.cur_function = content[20:26]
                token = \'\'
                f.class_name = class_name
                f.var = var_name 
                i = i + 1
                
            if \'eval\' in content:
                f.bool_cur = 1
                if \'=\\\'\' in last_content:
                    f.bool_cur = 2
                if \'.\\\'\' in last_last_content:
                    num_content = last_last_last_content
                    if \'>\' in last_last_last_content:
                        num1_before_position = num_content.find(\'if(\')
                        num1_after_position = num_content.find(\'>\')
                        num2_after_position = num_content.find(\')\')
                        num1 = num_content[num1_before_position+3:num1_after_position]
                        num1 = int(num1)
                        num2 = num_content[num1_after_position+1:num2_after_position]
                        num2 = int(num2)
                        if num1 > num2:
                            f.bool_cur = 2    
                
            if \'method_exists\' in content:
                f.next_function.append(content[62:68])
                j = j + 1
                k = k + 1
                f.bool_next = k
                if \'=\\\'\' in last_content:
                    f.token = 1
                if \'.\\\'\' in last_last_content:
                    num_content = last_last_last_content
                    if \'>\' in last_last_last_content:
                        num1_before_position = num_content.find(\'if(\')
                        num1_after_position = num_content.find(\'>\')
                        num2_after_position = num_content.find(\')\')
                        num1 = num_content[num1_before_position+3:num1_after_position]
                        num1 = int(num1)
                        num2 = num_content[num1_after_position+1:num2_after_position]
                        num2 = int(num2)
                        if num1 > num2:
                            f.token = 1    
            else:
                if \'$this->\' in content:
                    next_position = content.find(\'$this->\')
                    true = content.find(\'->\',next_position+7)
                    if true != -1:
                        f.next_function.append(content[next_position+16:next_position+22])
                        j = j + 1
                        k = k + 1
                        f.bool_next = k
                    if \'=\\\'\' in last_content:
                        f.token = 1
                    if \'.\\\'\' in last_last_content:
                        num_content = last_last_last_content
                        if \'>\' in last_last_last_content:
                            num1_before_position = num_content.find(\'if(\')
                            num1_after_position = num_content.find(\'>\')
                            num2_after_position = num_content.find(\')\')
                            num1 = num_content[num1_before_position+3:num1_after_position]
                            num1 = int(num1)
                            num2 = num_content[num1_after_position+1:num2_after_position]
                            num2 = int(num2)
                            if num1 > num2:
                                f.token = 1        

t = 0

#处理数据

def paixu(content,keyword,t):    
    position = tree_content.find(\'cur \'+keyword)
    token_position = tree_content.find(\'token \',position)
    token = tree_content[token_position+6:token_position+7]
    token = int(token)
    if token == 1:
        return 0
    pre_content = content + keyword +\'-->\'
    post_cur = tree_content.find(\'bool_cur\',position)
    current = tree_content[post_cur+9:post_cur+10]
    current = int(current)
    if current == 2:
        return 0
    if current == 1:
        print(\'yes  \'+pre_content)
        r_file.write(\'yes  \')
        r_file.write(pre_content+\'\\n\')
        r_file.write(\'\\n\')
        return 0
    if t > 30:
        print(\'no  \'+pre_content)
        r_file.write(pre_content+\'no\\n\')
        return 0


    key_position = tree_content.find(\'f \',position)
    keyword = tree_content[key_position+2:key_position+8]             
    post_next = tree_content.find(\'bool_next\',position)
    num = tree_content[post_next+10:post_next+11]
    num = int(num)
    while num >= 1:
        t = t + 1
        paixu(pre_content,keyword,t)
        key_position = tree_content.find(\'f \',key_position+1)
        keyword = tree_content[key_position+2:key_position+8]
        num = num - 1
        t = t - 1


    


    
content = \'\'

# read()

r_file=open(\'result.txt\',\'w\')
with open(\'tree.txt\') as w_file :
    keyword = \'qZ5gIM\'
    tree_content = w_file.read()
    position = tree_content.find(keyword)    
    content = keyword + \'-->\'
    key_position = tree_content.find(\'f \',position)
    keyword = tree_content[key_position+2:key_position+8]
    post_next = tree_content.find(\'bool_next\',position)
    num = tree_content[post_next+10:post_next+11]
    num = int(num)
    while num >= 1:
        t = t + 1
        paixu(content,keyword,t)
        key_position = tree_content.find(\'f \',key_position+1)
        keyword = tree_content[key_position+2:key_position+8]
        num = num - 1

我将所有有拼接的数据全部过滤，最后结果是没有，可能是我代码还有问题，也有可能本身就是希望过滤拼接字符来实现pop链

发布于2021-09-18 17:01:36

16赞

0条评论

安全客

商务合作

内容需知

投稿须知
转载须知
官网QQ群：568681302

合作单位

程序分析理论 初实践初探索