前言
N1CTF 2021中主要有4道考察Crypto方向的题目,题目整体难度相对较高,在这里对这4道题目进行一下分析。
checkin
| Name | Category | Points | Solves |
|---|---|---|---|
| checkin | CRYPTO | 624 / 1000 | 7 |
题目描述
None
题目描述
本题中未知量x的表达式为:
x = 2021 * p + 1120 * q
且未知量x和已知量h满足:
x + x^(-1) ≡ h (MOD N)
同余式两边同乘x,移项,得:
x^2 + 1 - h * x ≡ 0 (MOD N)
同时本题还提供了512位素数p的高22位p_0,那么我们借助p_0计算出x的一个近似估计x_approx:
x_approx = 2021 * (p_0 << 490) + 1120 * (N // (p_0 << 490))
x同该近似估计x_approx之间的误差x_diff约为500位,如果我们将x_diff看作一个新的未知量,根据x和h的模N同余方程,此时我们可以设关于x_diff的模N多项式f为:
f(x_diff) = (xx + x_diff)^2 + 1 - h * (xx + x_diff)
此时500位左右的x_diff可以看成模N同余方程f(x_diff) ≡ 0 (MOD N)的一个小整数解,我们可以使用CopperSmith攻击求出。
这里需要注意得是,SageMath中small_roots方法的epsilon参数的默认值为0.05,该默认参数下的bound不足以解出本题的小整数解,根据1/2 * N^(beta^2 // delta - epsilon)我们可以直接调整epsilon的值为0.01,但是此时small_roots方法将会在100×102的矩阵上应用LLL算法,造成非常大的时间开销,我们可以在此基础上进行调参,经过测试,将epsilon的值略上调为0.02后,此时small_roots方法可以在约1 min内完成计算,得到x_diff之后,将其加上x_approx即可得到x。
拿到x的值后,此时联立x = 2021 * p + 1120 * q和N = p * q即可分解N,继而计算出私钥d、解密FLAG的密文拿到FLAG。
解题脚本
#!/usr/bin/env sage
from Crypto.Util.number import long_to_bytes
N = 124592923216765837982528839202733339713655242872717311800329884147642320435241014134533341888832955643881019336863843062120984698416851559736918389766033534214383285754683751490292848191235308958825702189602212123282858416891155764271492033289942894367802529296453904254165606918649570613530838932164490341793
ct = 119279592136391518960778700178474826421062018379899342254406783670889432182616590099071219538938202395671695005539485982613862823970622126945808954842683496637377151180225469409261800869161467402364879561554585345399947589618235872378329510108345004513054262809629917083343715270605155751457391599728436117833
h = 115812446451372389307840774747986196103012628652193338630796109042038320397499948364970459686079508388755154855414919871257982157430015224489195284512204803276307238226421244647463550637321174259849701618681565567468929295822889537962306471780258801529979716298619553323655541002084406217484482271693997457806
p_0 = 4055618
p_approx = p_0 << 490
x_approx = 2021 * p_approx + 1120 * (N // p_approx)
P.<x_diff> = PolynomialRing(Zmod(N))
f = (x_approx + x_diff)^2 + 1 - h * (x_approx + x_diff)
res = f.small_roots(X = 2^500, epsilon = 0.02)
x_diff = Integer(res[0])
x = x_approx + x_diff
assert (h == (inverse_mod(x, N) + x) % N)
p = var('p')
q = var('q')
res = solve([x == 2021 * p + 1120 * q, N == p * q], p, q)
p = Integer(res[0][0].rhs())
q = Integer(res[0][1].rhs())
assert (p * q == N)
d = inverse_mod(65537, (p - 1) * (q - 1))
pt = pow(ct, d, N)
FLAG = long_to_bytes(pt)
print(FLAG)
# n1ctf{093fd4c4-5cc9-427e-98ef-5a04914c8b4e}
n1ogin
| Name | Category | Points | Solves |
|---|---|---|---|
| n1ogin | CRYPTO | 624 / 1000 | 7 |
题目描述
To prevent any adversary sitting in the middle from eavesdropping, we apply hybrid encryption in our n1ogin system.
nc 43.155.59.224 7777
题目描述
本题中提供给选手了一份管理员成功登陆系统的流量,在该系统中,传递的消息使用AES-CBC进行加密,其中AES的密钥使用RSA进行加密,需要选手获得管理员的密码来通过管理员身份登陆系统,继而执行flag命令来拿到FLAG。
审计服务器端源码可以发现,在对AES进行解密处理时,引入了各种报错提示,其中就包括对PKCS #7 padding的报错提示,如果我们可以获取到该报错提示,那么只需对系统进行标准的AES-CBC padding oracle attack攻击即可解密密文拿到管理员密码,但是问题在于本题中服务器端在输出消息报错时,不管对于哪种类型的错误,均只提示一种错误,因此我们需要找到一种方法,能够根据这一错误提示来获取关于padding是否正确的信息。
经过分析可以发现,如果服务器端通过了padding check,那么接下来就会进入到mac check环节,而在mac check环节中,进行了7777次哈希运算,这一过程显然会引入一个比较明显的时间开销,而如果没有通过padding check的话,则会直接报错,即跳过了mac check环节,那么时间开销就会显著减少,因此我们可以根据服务器返回报错的时间,来判断padding是否正确,即借助基于时延的侧信道攻击(timing based side channel attack)来构造出一个padding oracle,接下来再利用CBC padding oracle恢复出明文拿到管理员密码即可。
这里有两个需要注意的地方,一个是在进行侧信道攻击时,由于服务器的响应时间每次存在差异,因此容易出现False Positive,为了减少这种偶然事件对攻击的影响,我们可以对每次消息重复发送若干轮,只有每一轮的时间开销都大于我们设置的阈值,才视为padding check通过的情况,而只要有一轮时间开销小于阈值,即视为padding check失败的情况,从而提高正确率;再一个需要注意的地方是由于明文较长,加上我们前面引入轮数之后会增加时间开销,因此恢复过程相对较慢,但是这里我们不需要恢复全部明文,注意到的管理员的密码字段正好在明文的末尾,而我们的padding oracle攻击又正好是从最后一个字节开始逐字节向前恢复,因此只需等到管理员密码恢复后即可。
解题脚本
#!/usr/bin/env python3
import time
import json
from pwn import *
from tqdm import tqdm
from client import *
IP = b"43.155.59.224"
PORT = 7777
BLOCK_SIZE = 16
# You need to debug this value according to the delay of communication with the server in your environment.
THRESHOLD = 0.10
# Increase the number of rounds to reduce false positives.
ROUNDS = 10
# Get from `packet.pcapng`
PACKET = {"rsa_data": "391b06a1740b8c9cf1c8d2bb66ba5b191caa8534b4be18c22ce81069658dd2cd3ca3a8d1a3fc8dfab4b68a6b076bf89be807404e0a98dd1bf9daaf8ba34e0556131d3e56cae61c0302d24a177481209e82de7ecf91c2fe66aa39162d7af9c2fdabaf0c444badfc6b82b071fda8e3b26d4d3e57dba25c36298601ae0153c73b7469c472ac4702531c38849772e7c6e24313e6eb7def64a7bec1c21150c1fded52b3ca716d4444b4d75836dff8c92a371f6256ee7a48034f6d5ea949d982f9f05c04d3d7cce10bd11b806cc02088b42fa0cb069390700fb586287ba224ea0b210ebd0479a4f1d2ef5f914bcc861125b7d8d714cf0feecb515c1b1ef869e91ca179", "aes_data": "1709bf9489f6df6dc31491cee4711f7a2a3e050f1ed3e9772442e8a8483e341313713383dd31fbf0133d55e977b8edf54ba832002ee4ee52da32c260b083a35b01626201c36dad6fca7b2be2aa03d90bf5c9a601a24149f55cdcd39f0bf6a032bfabeebee5259a21e188f5c5f8776cd9d7c072054781169174bddbc390e6da21bd7b85f76c93f48914fb1958ac89e464511d9a17fb2174aab825cb13eb3f0dfa"}
def send_data(io, data):
time_start = time.time()
io.sendlineafter(b"> ", json.dumps(data))
_ = io.recvline()
time_end = time.time()
return time_end - time_start
def timing_attack(io, data):
for _ in range(ROUNDS):
time_diff = send_data(io, data)
if time_diff > THRESHOLD:
continue
else:
return False
return True
def oracle(io, ct, mac):
data = {"rsa_data" : PACKET["rsa_data"], "aes_data" : (ct + mac).hex()}
return timing_attack(io, data)
def cbc_padding_oracle_attack(io, ct, mac):
ct_blocks = [ct[i:i + BLOCK_SIZE] for i in range(0, len(ct), BLOCK_SIZE)]
pt = b''
for idx in range(1, len(ct_blocks)):
known_ct_block = b''
for pad_len in range(1, BLOCK_SIZE + 1):
for x in tqdm(range(256)):
new_ct_block = bytes([x]) + known_ct_block
new_ct_blocks = ct_blocks[:-idx - 1] + [os.urandom(BLOCK_SIZE - pad_len) + new_ct_block] + [ct_blocks[-idx]]
new_ct = b''.join(new_ct_blocks)
if oracle(io, new_ct, mac):
pt += bytes([pad_len ^ ct_blocks[-idx - 1][-pad_len] ^ x])
known_ct_block = bytes([i ^ pad_len ^ (pad_len + 1) for i in new_ct_block])
print(pt[::-1])
break
return pt[::-1]
aes_data = bytes.fromhex(PACKET["aes_data"])
ct, mac = aes_data[:-16], aes_data[-16:]
io = remote(IP, PORT)
_ = io.recvline()
# We don't need to recover the whole plaintext, just stop the process when the password is recovered.
pt = cbc_padding_oracle_attack(io, ct, mac)
password = b"R,YR35B7^r@'U3FV"
login(io)
'''
username: admin
password: R,YR35B7^r@'U3FV
admin login ok!
[*] Switching to interactive mode
admin@local> flag
n1ctf{R3m0t3_t1m1ng_4ttack_1s_p0ssibl3__4nd_u_sh0uld_v3r1fy_th3_MAC_f1rs7}
'''
n1token1
| Name | Category | Points | Solves |
|---|---|---|---|
| n1token1 | CRYPTO | 833 / 1000 | 3 |
题目描述
None
题目描述
本题中采用了类似Rabin解密的运算过程来生成token,对于密文c、每个token t_i和每个随机数X_i,有:
t_i^2 ≡ c^2 * X_i (MOD N)
其中每个X_i均由若干素数累乘而来,直到其比特数大于920,这里的素数来自前10000个素数中随机挑选920个素数所构成的集合。相较于1024比特的c和t_i来讲,这里X_i的比特数相对较小,因此我们可以将其看作一个HNP(Hidden Number Problem)问题,通过LLL格基规约来计算出每个X_i。
将上述同余式X_i单独作为方程一侧并改写成等式,有:
X_i = t_i^2 * c^(-2) + k_i * N
我们可以列出920个这样的方程,但是这对于LLL算法来讲维数太大了,我们只需选取其中部分进行格基规约即可,以取前64个方程为例,将其用矩阵形式表示,有:
计算出前64个X_i的值后,我们可以任取其中一个计算出c^2 MOD N的值,继而恢复整个X_i的序列。接下来,为了解密密文,我们需要分解N,根据二次同余的推论:
x^2 ≡ y^2 (MOD N) -> x ≡ k * y (MOD N)
其中k满足:
k^2 ≡ 1 (MOD N)
将同余式写成等式:
(k - 1) * (k + 1) = g * N = g * p * q = (g_0 * p) * (g_1 * q)
因此当k不等于1或-1时,我们可以通过计算gcd(k - 1, p)和gcd(k + 1, q)来计算出p和q的值继而分解N。
接下来我们利用这一方法从我们已有的表达式中计算出这样的一个k来分解N,对于我们本题中的920组数据:
t_0^2 ≡ c^2 * X_0 (MOD N)
t_1^2 ≡ c^2 * X_1 (MOD N)
...
t_919^2 ≡ c^2 * X_919 (MOD N)
如果我们从其中选取w个表达式相乘,当w为偶数时,那么同余式左边由t_i^2累乘得到的项可以看成(t_0 * t_1 * ... * t_w)^2,同余式右边由c^2累乘得到的项可以看成(c^w)^2,当剩下的这w个X_i相乘得到的项也可以写为一个项的平方时,我们即构造出了一个上面所提到的分解N所需的表达式,由于这里t_i、X_i和c^2在模N下的值我们均已知,因此我们可以直接计算出k的值,继而按照上面的方法分解N,因此接下来我们只需从这920组数据当中找出符合条件的w组即可。
为了找到这样的w组数据,我们可以将每个X_i展开为若干素数prime_i乘积的形式,然后记录下每个prime_i的指数的奇偶性,这样一来可以将其看作一个GF(2)上的920维行向量,由于我们有920组数据,因此可以列出一个920 * 920的矩阵,这样一来寻找若干X_i相乘的结果其指数为偶数的问题就转化为了寻找若干prime_i其指数之和在GF(2)下为0的问题,因此我们直接对该矩阵求left kernel matrix即可,这样一来我们可以得到若干组res向量,其中每一个res向量中值为1的下标对应着我们的920组数据当中应当选取的X_i的下标,同时为了保证w为偶数,我们还需要选择res向量中1的个数为偶数的向量,在本题的数据中,我们一共得到了两组res向量,其中一组中1的个数为奇数、一组中1的个数为偶数,我们选择偶数这组即可,然后按照上述过程计算出k,既而即可分解N求出私钥d。
最后由于我们目前知道的仅为c^2 MOD N的值,因此我们可以先对其做rabin解密,拿到4组可能的c的值,再依次对其做RSA解密从其中找到FLAG即可。
解题脚本
#!/usr/bin/env python3
import re
from Crypto.Util.number import long_to_bytes, sieve_base
def rabin_decrypt(ct, sk, N):
p, q = sk
inv_p = inverse_mod(p, q)
inv_q = inverse_mod(q, p)
m_p = power_mod(ct, (p + 1) // 4, p)
m_q = power_mod(ct, (q + 1) // 4, q)
a = (inv_p * p * m_q + inv_q * q * m_p) % N
b = N - a
c = (inv_p * p * m_q - inv_q * q * m_p) % N
d = N - c
return [a, b, c, d]
f = open("output.txt", "r")
N = Integer(re.findall(r"\d+", f.readline())[0])
token_list = [Integer(re.findall(r"\d+", f.readline())[1]) for _ in range(920)]
token_square_list = [power_mod(i, 2, N) for i in token_list]
SIZE_0 = 64
SIZE_1 = 920
M = identity_matrix(ZZ, SIZE_0) * N
M = M.stack(vector(ZZ, token_square_list[: SIZE_0]))
res = M.LLL()
X_list = []
X_list.append(res[1][0])
c_square = (token_square_list[0] * inverse_mod(X_list[0], N)) % N
X_list = X_list + [Integer((token_square_list[i] * inverse_mod(c_square, N)) % N) for i in range(1, SIZE_1)]
prime_list = []
for prime in sieve_base:
for X in X_list:
if X % prime == 0:
prime_list.append(prime)
break
A = list(matrix(ZZ, 920, 920))
for i in range(len(X_list)):
for prime, exponent in list(factor(X_list[i])):
A[i][prime_list.index(prime)] = exponent
A = matrix(GF(2), A)
res_list = A.left_kernel().basis()
res = 0
for i in range(len(res_list)):
if list(res_list[i]).count(1) % 2 == 0:
res = res_list[i]
break
cnt = list(res).count(1)
token_square_pro = 1
X_pro = 1
for i in range(SIZE_1):
if res[i] == 1:
token_square_pro *= token_list[i]
X_pro *= X_list[i]
X_pro_sqrt = X_pro.nth_root(2, True)[0]
k = (((token_square_pro * inverse_mod(X_pro_sqrt, N)) % N) * power_mod(c_square, -(cnt // 2), N)) % N
p = gcd(k - 1, N)
q = gcd(k + 1, N)
assert is_prime(p) and is_prime(q)
assert p * q == N
ct_list = rabin_decrypt(c_square, (p, q), N)
for ct in ct_list:
d = inverse_mod(65537, (p - 1) * (q - 1))
pt = power_mod(ct, d, N)
FLAG = long_to_bytes(pt)
if FLAG.startswith(b"n1ctf"):
print(FLAG)
# n1ctf{b9e7d419-0df8-438a-9120-efdf3ddf155f}
n1token2
| Name | Category | Points | Solves |
|---|---|---|---|
| n1token2 | CRYPTO | 833 / 1000 | 3 |
题目描述
None
题目描述
设本题中y = f(x)的表达式为:
f(x) ≡ e + SECRET_0 * x + SECRET_1 * x^2 + ... + SECRET_15 * x^16 (MOD p)
我们已知f(1)至f(250)共计250个式子的值,但是在每一个式子中,e为[1, 20, 113, 149, 219]中的一个随机值,这里有些类似LWE(learning with erros)的场景,由于引入了错误e的存在,因此我们不能直接在此基础上通过解方程来拿到SECRET的值。
虽然我们不能直接解方程,但是我们可以构造一个新的方程,不管每次e的值为多少,必有:
(f(x) - e_0) * (f(x) - e_1) * (f(x) - e_2) * (f(x) - e_3) * (f(x) - e_4) ≡ 0 (MOD p)
即:
A_i * f(x)^5 + B_i * f(x)^4 + C_i * f(x)^3 + D_i * f(x)^2 + E_i * f(x) + F_i ≡ 0 (MOD p)
如果此时我们变化一下,将f(x)中的系数SECRET看成未知数,将f(x)到f(x)^5看成5个独立的多项式,由于f(x)中包含16个单项,那么上式共引入(16 + 1) + (32 + 1) + (48 + 1) + (64 + 1) + (80 + 1) = 245项,因此我们可以列出一个245 * 250的系数矩阵,该矩阵的每一行分别由E_i、D_i、C_i、B_i和A_i同这(16 + 1)、(32 + 1)、(48 + 1)、(64 + 1)和(80 + 1)项相乘构造而来,而该系数矩阵对应的同余方程右侧的值向量中的每个值即为(-F_i) % p = p - F_i,然后我们直接在模p下解该方程组,取结果的下标为1到16的项即为SECRET,继而恢复出FLAG。
解题脚本
#!/usr/bin/env sage
from Crypto.Util.number import long_to_bytes
p = 251
e = [1, 20, 113, 149, 219]
y = list(bytes.fromhex("1d85d235d08dfa0f0593b1cfd41d3c98f2a542b2bf7a614c5d22ea787e326b4fd37cd6f68634d9bdf5f618605308d4bb16cb9b9190c0cb526e9b09533f19698b9be89b2e88ba00e80e44d6039d3c15555d780a6a2dbd14d8e57f1252334f16daef316ca692c02485684faee279d7bd926501c0872d01e62bc4d8baf55789b541358dfaa06d11528748534103a80c699a983c385e494a8612f4f124bd0b2747277182cec061c68197c5b105a22d9354be9e436c8393e3d2825e94f986a18bd6df9ab134168297c2e79eee5dc6ef15386b96b408b319f53b66c6e55b3b7d1a2a2930e9d34287b74799a59ab3f56a31ae3e9ffa73362e28f5751f79"))
P.<x> = PolynomialRing(GF(p))
M = [[] for _ in range(p - 1)]
b = []
for x_v in range(p - 1):
f = (x + e[0] - y[x_v]) * (x + e[1] - y[x_v]) * (x + e[2] - y[x_v]) * (x + e[3] - y[x_v]) * (x + e[4] - y[x_v])
coeff = f.coefficients(sparse = False)
M[x_v] += [(coeff[1] * power_mod(x_v + 1, i, p)) % p for i in range(16 + 1)]
M[x_v] += [(coeff[2] * power_mod(x_v + 1, i, p)) % p for i in range(32 + 1)]
M[x_v] += [(coeff[3] * power_mod(x_v + 1, i, p)) % p for i in range(48 + 1)]
M[x_v] += [(coeff[4] * power_mod(x_v + 1, i, p)) % p for i in range(64 + 1)]
M[x_v] += [(coeff[5] * power_mod(x_v + 1, i, p)) % p for i in range(80 + 1)]
b.append(p - coeff[0])
M = matrix(GF(p), M)
b = vector(GF(p), b)
res = M.solve_right(b)
SECRET = b''.join(map(lambda x: bytes([x]), res[1: 16 + 1]))
FLAG = "n1ctf{" + SECRET.hex() + "}"
print(FLAG)
# n1ctf{c5cc7404dc79e7a9d57ab19040a82f5a}


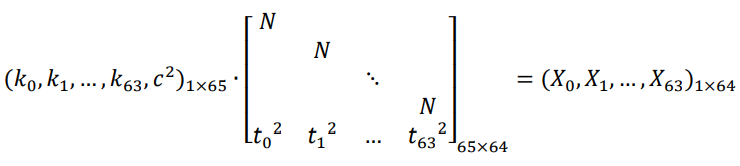







发表评论
您还未登录,请先登录。
登录