0x01 RSA概要
RSA算法是非对称密码算法。非对称密码又称为公钥密码，意思为每对加密包含一个公钥（可能为他人所知）和一个私钥（可能不为所有人所知）。有效的安全需要保持私钥的私密性；公钥可以在不影响安全性的情况下公开分发。
RSA 的安全性依赖于分解两个大素数乘积的实际困难，但相对较慢，可以称为“分解问题”。
RSA应用
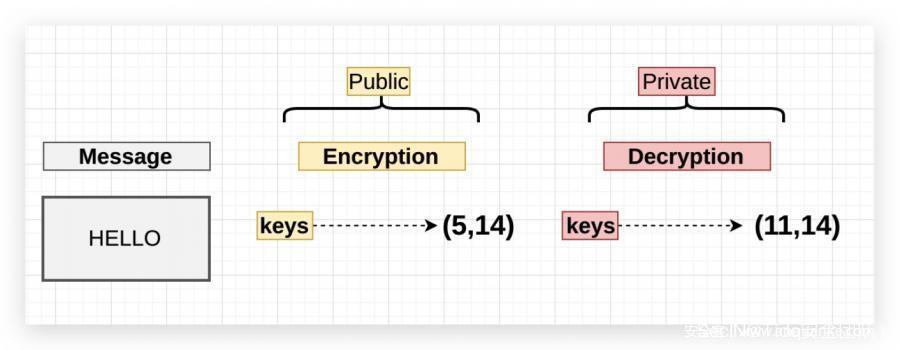
- 客户端将其公钥发送到服务器并请求一些数据
- 服务器使用客户端的公钥加密数据并发送加密数据
- 客户端接收此数据并对其进行解密
0x02 RSA算法详细流程
RSA算法四个步骤
- 密钥生成
- 密钥分发
- 加密
- 解密
关于RSA相关公式
n = p * q
(n) = (p – 1) * (q – 1)
ed 1 mod (n)
c = m**e mod n
m = c**d mod n
simple example
已知：P = 11，q = 29，e = 3
求d
通过公式：
(n) = (p – 1) * (q – 1)
(n) = (p-1)(q-1) = (11-1)*(29-1) = 280
通过公式：
ed 1 mod (n)
如果两个整数 ed 和 1 满足 ed-1 能被 (n) 整除，称为整数 ed 与 1 对模 (n) 同余
1 < d < (n)
3d 1 mod 280
3d mod 280 = 1
d = 187
通过公式：
n = p * q
n = 11 * 29 = 319
公钥（n，e）
私钥（n，d）
得到：
公钥（319，3）
私钥（319，187）
或者用脚本解d：
gmpy2.invert(e,(p-1)*(q-1))
使用此密钥对可以加密的最大数字是多少
加密函数为：
c(m) = m^e mod n
解密函数为：
m(c) = c^d mod n
RSA算法一次能加密的名文长度与密钥长度成正比。
len_in_byte(raw_data) = len_in_bit(key)/8-11
如果小于这个长度，就需要进行数据补齐，称为padding，不进行数据补齐用户就无法确分解密后内容的真实长度。
n的长度就是密钥长度，n = 319，n的二进制为100111111，密钥为9位，RSA实际可加密的明文长度最大也是1024bits
当加密明文m = 23时，求密文c
加密函数为：
c(m) = m^e mod n
c(m) = 23^3 mod 319 = 12167 mod 319
c(m) = 45
import gmpy2
n = 319
e = 3
m = 23
print(pow(m, e, n))
当密文c = 23时，求明文m
解密函数为：
m(c) = c^d mod n
m(c) = 23^187 mod 319
m(c) = 199
import gmpy2
n = 319
d = 187
c = 23
print(pow(c,d,n))
发表评论
您还未登录，请先登录。
登录