0x01 摘要
每次碰到RSA题都是一脸蒙逼,这次专门来撸一撸RSA加密算法。
0x02 前言
CTF里考RSA算法是比较常见的。可惜每次碰到都一脸蒙逼,最心酸的是Writeup就摆在那里,不离不弃,而我的智商摆在那里,不高不低。
0x03 理解RSA
最重要一步,当然是理解RSA算法,理解了,就什么都不难了。
1977年,三位数学家Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密。这种算法用他们三个人的名字命名,叫做RSA算法。从那时直到现在,RSA算法一直是最广为使用的"非对称加密算法"。毫不夸张地说,只要有计算机网络的地方,就有RSA算法。
这种算法非常可靠,密钥越长,它就越难破解。根据已经披露的文献,目前被破解的最长RSA密钥是768个二进制位。也就是说,长度超过768位的密钥,还无法破解(至少没人公开宣布)。因此可以认为,1024位的RSA密钥基本安全,2048位的密钥极其安全。
举例子的时候一般出现的人物都是Bob和Alice。
比如有两个用户Alice和Bob,Alice想把一段明文通过双钥加密的技术发送给Bob,Bob有一对公钥和私钥,那么加密解密的过程如下:
Bob将他的公开密钥传送给Alice。
Alice用Bob的公开密钥加密她的消息,然后传送给Bob。
Bob用他的私人密钥解密Alice的消息。
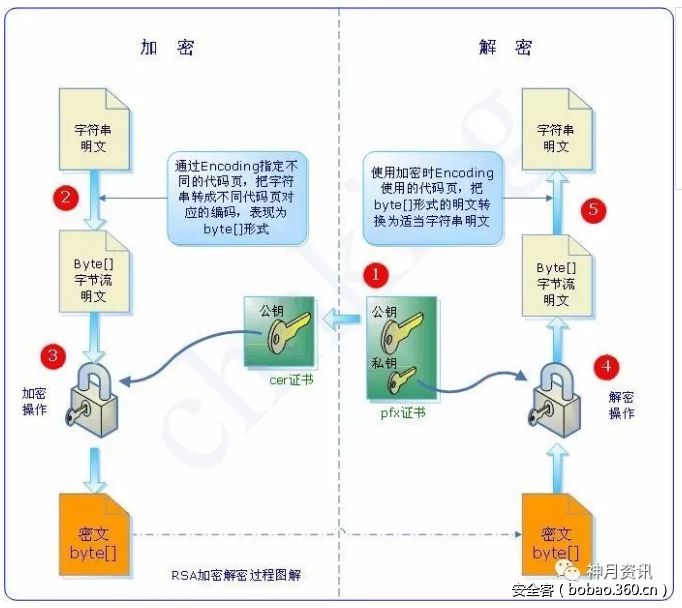
上面的过程可以用下图表示,Bob先生成公钥和私钥,Alice使用Bob的公钥进行加密,Bob用自己的私钥进行解密。
总结:
公钥和私钥是成对的,它们互相解密。
公钥加密,私钥解密。
私钥数字签名,公钥验证。
0x03.1.1 数学概念
要看算法了,还是先温习一下基本的概念吧,哈哈,忘的人可以看看,大神可以跳过。
0x03.1.1.1 互质关系
如果两个正整数,除了1以外,没有其他公因子,我们就称这两个数是互质关系(coprime)。比如,15和32没有公因子,所以它们是互质关系。这说明,不是质数也可以构成互质关系。
关于互质关系,不难得到以下结论:
1.任意两个质数构成互质关系,比如13和61。
2.一个数是质数,另一个数只要不是前者的倍数,两者就构成互质关系,比如3和10。
3.如果两个数之中,较大的那个数是质数,则两者构成互质关系,比如97和57。
4.1和任意一个自然数是都是互质关系,比如1和99。
5.p是大于1的整数,则p和p-1构成互质关系,比如57和56。
6.p是大于1的奇数,则p和p-2构成互质关系,比如17和15。
0x03.1.1.2 欧拉函数
欧拉函数求的是什么呢?
即:任意给定正整数n,请问在小于等于n的正整数之中,有多少个与n构成互质关系?(比如,在1到8之中,有多少个数与8构成互质关系?)
其中,在1到8之中,与8形成互质关系的是1、3、5、7,所以 φ(n) = 4。
常用的运算过程有:
φ(n)= φ(p×q)=φ(p)φ(q)=(p-1)(q-1)
欧拉公式:
例子:
1323的欧拉函数就是756。
0x03.1.1.3 欧拉定理
如果两个正整数a和n互质,则n的欧拉函数φ(n) 可以让下面的等式成立:
也就是说,a的φ(n)次方被n除的余数为1。或者说,a的φ(n)次方减去1,可以被n整除。
比如,3和7互质,而7的欧拉函数φ(7)等于6,所以3的6次方(729)减去1,可以被7整除(728/7=104)。
0x03.1.1.4 费马小定理
假设正整数a与质数p互质,因为质数p的φ(p)等于p-1,则欧拉定理可以写成:
0x03.1.1.5 模反元素
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1。
这时,b就叫做a的"模反元素"。
而我们的RSA中,e和b就互为模反元素。
0x03.1.2 算法
RSA算法涉及三个参数,n,e,d,私钥为(n,d),公钥为(n,e)。
其中n是两个大素数p,q的乘积。
d是e的模反元素,φ(n)是n的欧拉函数。
c为密文,m为明文,则加密过程如下:
解密过程如下:
n,e是公开的情况下,想要知道d的值,必须要将n分解计算出n的欧拉函数值,而n是两个大素数p,q的乘积,将其分解是困难的。
上面的内容可以用一个图表示:
0x03.1.3 举例
看一遍运算过程,知道怎么用是最快的学习方法哈哈。假设用户A需要将明文“key”通过RSA加密后传递给用户B。
0x03.1.3.1 设计公私钥(n,e),(n,d)
1)p、q、n
令p=3,q=11,得出n=p×q=3×11=33;(质数p和q越大越难破解,n转成二进制后的长度就是密钥长度)
2)φ(n)
φ(n)=(p-1)(q-1)=2×10=20;
3)e和d
选一个1到φ(n)之间的质数,这里取e=3,(3与20互质)则e×d≡1 (modφ(n)),即3×d≡1(mod 20)。令x=d,20的倍数为-y,则3x-20y=1。求解得:x=7,y=1。
因此,当d=7时,e×d≡1 modφ(n)同余等式成立。从而我们可以设计出一对公私密钥,加密密钥(公钥)为:KU=(n,e)=(33,3),解密密钥(私钥)为:KR=(n,d)=(33,7)。
0x03.1.3.2 英文数字化
将明文信息数字化,并将每块两个数字分组。假定明文英文字母编码表为按字母顺序排列数值,即:
则得到分组后的key的明文信息为:11,05,25。
0x03.1.3.3 明文加密
用户加密密钥(33,3) 将数字化明文分组信息加密成密文。由C≡Me(mod n)得:
因此,得到相应的密文信息为:11,31,16。
0x03.1.3.4 密文解密
用户B收到密文,若将其解密,只需要计算,即:
用户B得到明文信息为:11,05,25。根据上面的编码表将其转换为英文,我们又得到了恢复后的原文“key”。
0x04 问题与思考
0x04.1 问题1:已经公钥(n,e),如何破解私钥(n,d)?
e*d≡1 (mod φ(n))。只有知道e和φ(n),才能算出d。
φ(n)=(p-1)(q-1)。只有知道p和q,才能算出φ(n)。
n=pq。只有将n因数分解,才能算出p和q。
如果n可以被因数分解,d就可以算出,也就意味着私钥被破解。
0x04.2 问题2:为什么n越大,就越难破解?
n的长度就是密钥长度。如3233写成二进制是110010100001,一共有12位,所以这个密钥就是12位。实际应用中,RSA密钥一般是1024位,重要场合则为2048位。
人类已经分解的最大整数(232个十进制位,768个二进制位)。比它更大的因数分解,还没有被报道过,因此目前被破解的最长RSA密钥就是768位。
0x04.3 问题3:为什么用n加密的明文长度要小于n,如果长度大于n如何加密?
根据互质关系第三条,如果两个数之中,较大的那个数是质数,则两者构成互质关系,比如97和57。
所以只要m<n,因为n为质数,m与n互质。
如果m>n,则将m分解成位数小于n的分组进行加密,解密后再组合起来。
0x05 CTF
下面列举了个CTF题,做着做着就会啦。目前只列举一道,当然还有其它很多攻击方法,像维纳攻击、广播攻击等等,就不班门弄斧了,进一步了解和学习可以看参考文章哈哈。
0x05.1 RSA Roll
例题来自【https://www.52pojie.cn/forum.php?mod=viewthread&tid=490769】
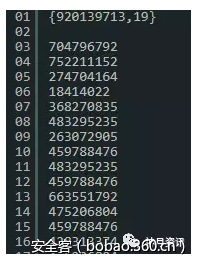
题目:
解答:
从上面可以看出,给出的是(n,e)=(920139713,19)和分组的密文。而这里的n明显不大,因此是可以破解的。
在线因数分解:【http://factordb.com/index.php?query=920139713】得到p=18443,q=49891
欧拉函数:φ(n) = (p-1)(q-1)=(49891-1)*(18443-1)=920071380
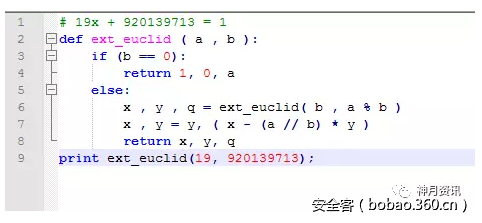
由此e=19, φ(n)= 920071380,e*d=1(modφ(n))即920071380x + 19y = 1
求解d:
得d=96849619,即(n,d)=(920139713,96849619),可以解那些密文了。
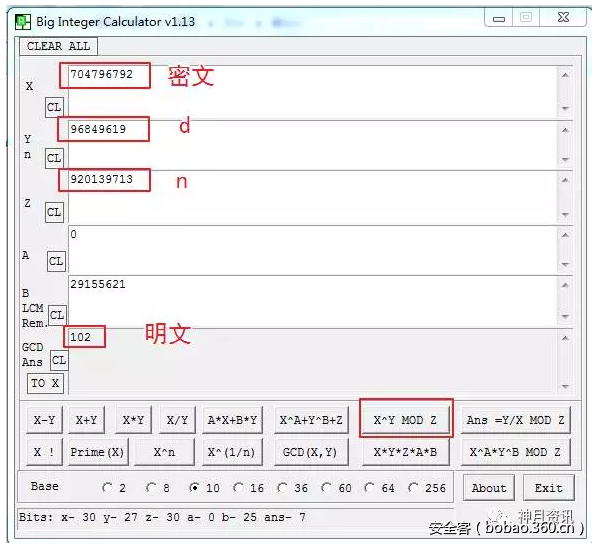
用【BigInt】求解:
如密文【704796792】
可以知道102的ascii码对应的是f,因此明文为f。其它的可以依次求解出来。
0x06 参考
RSA算法原理:
https://www.kancloud.cn/kancloud/rsa_algorithm/48484
欧拉函数:
https://zh.wikipedia.org/wiki/%E6%AC%A7%E6%8B%89%E5%87%BD%E6%95%B0
CTF中RSA的常见攻击方法:
http://bobao.360.cn/learning/detail/3058.html
CTFCrypto练习之RSA算法:
http://blog.csdn.net/qq_18661257/article/details/54563017
因数分解:
用实例给新手讲解RSA加密算法:



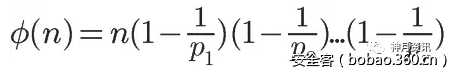
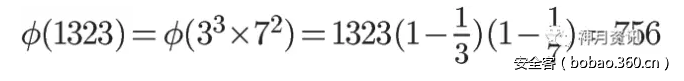
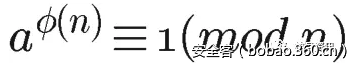
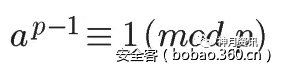
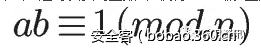
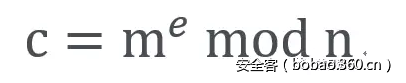
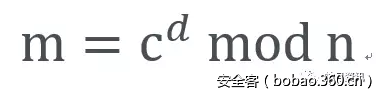











发表评论
您还未登录,请先登录。
登录