前言
在上一篇文章当中,我们对LFSR类题目的模型和考察方式做了一个基本的介绍,在这篇文章当中我们将进一步分析LFSR类题目的相关知识和技巧。
这篇文章中会涉及很多相关知识,为了让大家更好的吸收,我们直接用题目说话。
本篇前置知识
分组码
分组码是对每段长度为k的信息,以一定的规则增加r=n-k个校验元,组成长为n的序列,我们称这个序列为码字。
在GF(2)下,信息组共有2^k个,相应的,码字也有2^k个,我们称这个2^k码字的集合为(n,k)分组码。当校验元与信息元之间是线性关系时,我们称之为线性分组码,一般用[n,k]表示。
[n,k]线性分组码是定义在F2上的n维线性空间中的一个k维子空间,由于该线性子空间在加法运算下构成阿贝尔群,所以线性分组码也被称为群码。
[n,k]线性分组码的2^k个码字组成了一个k维子空间,因此这2^k个码字完全可由k个独立矢量所组成的基底张成。我们可以设基底为:
将这组基底写成矩阵的形式,则有:
[n,k]码中的任何码字都可以由这组基底的线性组合生成,即:
其中,m=(m1,m2,...,mk)是k个信息元组成的信息组。因此若已知信息组m,可通过上式求得相应的码字,称G为[n,k]码的生成矩阵。
为了让大家更好的吸收这些知识,我们直接用题目说话。
CTF例题演示
2019 0CTF/TCTF 线上赛 zer0lfsr
题目给出的脚本如下:
from secret import init1,init2,init3,FLAG
import hashlib
assert(FLAG=="flag{"+hashlib.sha256(init1+init2+init3).hexdigest()+"}")
class lfsr():
def __init__(self, init, mask, length):
self.init = init
self.mask = mask
self.lengthmask = 2**(length+1)-1
def next(self):
nextdata = (self.init << 1) & self.lengthmask
i = self.init & self.mask & self.lengthmask
output = 0
while i != 0:
output ^= (i & 1)
i = i >> 1
nextdata ^= output
self.init = nextdata
return output
def combine(x1,x2,x3):
return (x1*x2)^(x2*x3)^(x1*x3)
if __name__=="__main__":
l1 = lfsr(int.from_bytes(init1,"big"),0b100000000000000000000000010000000000000000000000,48)
l2 = lfsr(int.from_bytes(init2,"big"),0b100000000000000000000000000000000010000000000000,48)
l3 = lfsr(int.from_bytes(init3,"big"),0b100000100000000000000000000000000000000000000000,48)
with open("keystream","wb") as f:
for i in range(8192):
b = 0
for j in range(8):
b = (b<<1)+combine(l1.next(),l2.next(),l3.next())
f.write(chr(b).encode())
我们来分析一下这道题目,尽管这道题目是以class lfsr的形式给出的,但是相信大家还是可以很容易的分辨出来我们这道题目的反馈函数和我们上一篇文章中分析的CTF题目中的反馈函数是一样的,我们观察一下3个mask:
mask1 = 0b100000000000000000000000010000000000000000000000
mask2 = 0b100000000000000000000000000000000010000000000000
mask3 = 0b100000100000000000000000000000000000000000000000
不难发现,每个mask只有2位为1,剩下的全部为0,那么根据我们上一章的结论,我们有如下表达式:
到目前为止,似乎和我们上一章的题目没有什么区别,只不过是从求一个初始状态变成了求3个,如果这道题我们给出了三组初始状态对应的三组输出序列,那么这道题的解法和上一章的题目完全一样,我们直接应用就可以解这道题。
但是显然,这里并不是这么给出的,在输出序列这里,这道题不再是给出每个初始状态独立的初始序列,而是输出做了如下的混合运算:
b = (b<<1)+combine(l1.next(),l2.next(),l3.next())
那我们就来分析一下combine函数,我们可以看到该函数返回的结果为:
(x1*x2)^(x2*x3)^(x1*x3)
由于x1、x2、x3均为GF(2)上的数字,因此该表达式等价于:
(x1&x2)^(x2&x3)^(x1&x3)
写成数学表达式的形式,即:
我们尝试把所有结果枚举一下:
x1:0
x2:0
x3:0
result:0
x1:0
x2:0
x3:1
result:0
x1:0
x2:1
x3:0
result:0
x1:0
x2:1
x3:1
result:1
x1:1
x2:0
x3:0
result:0
x1:1
x2:0
x3:1
result:1
x1:1
x2:1
x3:0
result:1
x1:1
x2:1
x3:1
result:1
观察结果可以发现,当x1=0时,会对应四个result(即combine(x1,x2,x3))值,其中3个result值为0,一个为1,即x1和result相同的概率为0.75。同理,x2和x3也满足这一规律,这样一来我们就找到了一个很关键的要素,那就是单个x的值和combine之后的值相同的概率有0.75。
接下来我们引入一类攻击方法—Correlation Attacks(相关攻击),相关攻击最早由Siegenthaler提出,它的攻击思路是利用单个LFSR的输出序列和combine之后的LFSR的输出序列之间具有的一定的相关性这一特点,来还原LFSR的初始状态。后来,Meier和Staffelbach在此基础上,提出了一种更为快速的攻击方法,我们通常把它称为Fast Correlation Attacks(快速相关攻击),这也是我们本章要重点讲述的攻击方法。
2011年,Meier和Staffelbach发表了名为《Fast Correlation Attacks: Methods and Countermeasures》的重要论文,在这篇论文当中,提出了两种重要的快速相关攻击的手法(论文中分别叫做Algorithm A和Algorithm B,下文中将沿用这一称呼),这两种手法分别对应了两个流派:一次通过法和迭代译码法,但不管哪种方法,这里我们可以把这两种算法都归类为Meier-Staffelbach这样一个模型之下,在这个模型下的攻击手法,当单个LFSR的输出序列和combine之后的LFSR的输出序列之间的相关性大于0.53时,我们通常就认为满足这类攻击的条件了,因此我们本题中0.75的相关性就可以采用这类攻击手法。
这种攻击手法有一个特点,就是在抽头数量较少的时候,作用效果会比较明显,什么是抽头呢?其实很好理解,反馈函数中影响LFSR下一个状态的比特位就叫做一个抽头,那么在我们的题目中就是mask里为1的位了,mask里有几个1,我们就说这个LFSR有几个抽头,那么很明显我们题目当中给出的3个LFSR都各自有2个抽头,而我们这里所提到的快速相关攻击,在抽头数量小于10时一般会有比较好的攻击效果,这也是我们这道题目适合使用快速相关攻击的一个原因。
这里也教给大家一个比赛时快速检索论文的技巧,就是抓密码系统下的典型特征,然后以典型特征为关键词去检索论文,比如这都题的小抽头序列数就是一个切入点,如果你以这个为关键词进行检索,很快就可以搜出我们的《Fast Correlation Attacks: Methods and Countermeasures》这篇论文。在国际赛上,越来越多的密码题倾向于考察选手的论文检索能力、论文理解能力以及根据论文写出solver的能力,因此快速检索出关键论文是我们解题环节的重要一步。
接下来我们对Meier-Staffelbach模型进行一个描述,后面在提到算法A和算法B时,都默认建立在该模型之下:
设截取输出序列z的长度为N,抽头数为t,级数为L,LFSR序列的相关概率为q=1-p。
接下来我们来看一下这两个算法的流程:
算法A:
计算截取序列每比特所需要的平均方程数:
计算截取序列的比特的模二加(含有t个比特)和原LFSR序列的相应比特的模二加相同的概率s(q,t):
计算在m个方程中至少有h个方程成立的概率Q(q,m,h):
zn=un并且m个方程中至少有h个方程成立的概率为:
在这种条件下,zn=un的概率为:
然后我们求出一个最大的h,并记为hmax,使得如下表达式成立:
计算在L个比特中错误的平均数:
从下式中选取至少满足hmax个校验等式的L个比特:
将z这L个比特作为LFSR输出序列的对应位置的估计I0,由I0可以得到寄存器序列{un}的估计,根据{un}的估计和{zn}的相关性来判断I0是否正确。如果不正确,则对I0依次加上重量为1,2,3...n的向量,得到I0的修正值,重复这一过程,直到找到正确解。
算法B:
1.计算截取序列每比特所需要的平均方程数:
对{un}的任一比特un均可以得到如下m个校验等式:
其中bi是{un}中t个不同元素的和。把{zn}中对应位置的元素代入上式得:
设yi中t个不同位置的正确概率分别为q1,q2,...,qt,则有:
且si(q1,q2,...,qt,t):
当zn满足第i1,i2,...ih校验等式,而不满足j1,j2,...,jm-h校验等式时,有:
zn至多满足h个校验等式的概率为:
当zn=un,且至多满足h个校验等式的概率为:
当zn≠un,且至多满足h个校验等式的概率为:
若zn至多满足h个校验等式,则取补,z中取补元素个数的期望值为:
取补后错误的个数为:
取补后正确的个数为:
取补后正确比特位增加的概率为:
对给定的q、m,找出使得I(q,m,h)最大的h,记为hmax。
若I(q,m,h)<=0,表示该算法没有起到校正作用,算法失败。
若I(q,m,h)>0,则第一次迭代后,有:
对算法A和算法B进行对比分析,可以得到算法A和算法B各自的优缺点如下:
1.算法A:
优点:错误率接近0.75时攻击效果显著。
缺点:当抽头数量较多时,该攻击将逐渐退化为穷举攻击。
2.算法B:
优点:错误率接近0.5时攻击效果显著。
缺点:该攻击需要进行大量的双精度计算,计算量较大
那么接下来如何来实现Solver呢,诚然对于许多国际战队的职业密码手来讲,写Solver是一项重要技能,但是有些时候对于一些经典攻击,我们并没有重写的必要,一个典型的例子就是针对RSA的Lattice based attacks,包括Coppersmith attack和Boneh and Durfee attacks等等,我们已经可以找到很成熟的开源implementations,这种情况下就可以大大减少我们写Solver的难度。对于本题当中的Fast Correlation Attacks来讲,同样是一个经典的例子:开普敦大学(university of cape town)于2011年发布了一个关于快速相关攻击的项目,我们可以访问这个链接来获取到Linux下的实现方案,该项目中包含了很详细的攻击思想、设计流程和实现方案,我们可以采用该方案来快速施展一次标准的Fast Correlation Attacks。
解压完后根据README文件进行安装即可,但是在安装之前我们需要首先确保已安装GSL(GNU Scientific Library),如果没有的话我们按照下述方法首先安装GSL:
wget http://ftp.club.cc.cmu.edu/pub/gnu/gsl/gsl-1.9.tar.gz
tar -zxvf gsl-1.9.tar.gz
cd gsl-1.9
sudo ./configure
sudo make
sudo make install
之后我们再按照README文档的步骤进行安装即可,安装完成之后,我们首先将题目中给出的keystream文件移动到/fastcorrattack/src路径下,然后使用python在该路径下创建三个文件:
#!/usr/bin/env python3
with open('keystream','rb') as f:
keystream = f.read()
keystream = keystream.decode()
outputs = ""
for i in keystream:
a = ord(i)
b = '0'*(8 - len(bin(a)[2:])) + bin(a)[2:]
for j in b:
outputs += j
outputs = outputs.encode()
with open('init1','wb') as f1:
f1.write(b"0.75n65536n48n2n23n48n" + outputs)
with open('init2','wb') as f2:
f2.write(b"0.75n65536n48n2n14n48n" + outputs)
with open('init3','wb') as f3:
f3.write(b"0.75n65536n48n2n42n48n" + outputs)
接下来我来解释一下向文件中写入的参数的含义:
1.第一个写入的参数表示相关性,根据我们前面的描述,我们知道本题中该参数的值为0.75。
2.第二个写入的参数表示输出比特的个数,我们本题中keystream文件大小为8192字节,因此该参数的值为8192*8=65536。
3.第三个写入的参数表示该LFSR初始状态的位数,本题中为48。
4.第四个写入的参数表示抽头的个数,本题中为2。
5.后续的x个参数表示抽头的位置,其中x为抽头的个数
6.最后的参数表示输出的比特流,本题中即长度为65536的outputs
接下来我们使用该目录下的fca程序来计算初始状态,在我们执行./fca时,可能会出现如下的报错:
./fca: error while loading shared libraries: libgsl.so.0: cannot open shared object file: No such file or directory
这其实是由于我们刚刚安装好gsl后,由于gsl的动态链接库没有及时刷新,导致执行时没有识别到造成的,我们可以在/fastcorrattack/src路径下执行如下命令来check一下:
ldd fca
执行后可以看到执行结果为:
linux-vdso.so.1 (0x00007ffce6faf000)
libgsl.so.0 => not found
libgslcblas.so.0 => not found
libm.so.6 => /lib/x86_64-linux-gnu/libm.so.6 (0x00007fd41eb06000)
libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6 (0x00007fd41e945000)
/lib64/ld-linux-x86-64.so.2 (0x00007fd41ecb5000)
这里我们可以看到在libgsl.so.0和libgslcblas.so.0的地方显示的均为not found,此时我们执行如下命令:
sudo ldconfig
执行之后再次执行ldd fca命令,可以看到在libgsl.so.0和libgslcblas.so.0的地方已经可以正常显示出位置了:
linux-vdso.so.1 (0x00007ffdde982000)
libgsl.so.0 => /usr/local/lib/libgsl.so.0 (0x00007fad2317c000)
libgslcblas.so.0 => /usr/local/lib/libgslcblas.so.0 (0x00007fad23144000)
libm.so.6 => /lib/x86_64-linux-gnu/libm.so.6 (0x00007fad22fc1000)
libc.so.6 => /lib/x86_64-linux-gnu/libc.so.6 (0x00007fad22e00000)
/lib64/ld-linux-x86-64.so.2 (0x00007fad2337b000)
这样一来我们再执行./fca时就可以成功执行了,fca可以正常运行后,我们使用如下命令来获取每个LFSR独立的输出流:
./fca ./init1 > output1
./fca ./init2 > output2
./fca ./init3 > output3
执行成功之后,我们会在同目录下得到output1、output2和output3这三个文件,我们以output1为例,打开该文件查看一下其中的内容:
------------------------------------------
Derived Parameters:
------------------------------------------
Correlation Probability: 0.750
Expected num of corrected bits [N_c]: 11511.71143
Correction factor [F(p,t,d)]: 239.82732
Probability threshold: 0.400
Expected num bits below threshold: 14184
------------------------------------------
Round Iteration N_w
------------------------------------------
1 1 14792
------------------------------------------
2 1 5126
2 2 5177
2 3 5177
2 4 5177
2 5 5177
------------------------------------------
Converged on a LFSR Sequence
100100011111111010101110010010110100101000110011...
在该文件的最后一行我们会看到一个长度为65536位的01串,这个01串即为我们第一个FLSR独立的输出流,这里为了方便本文章页面显示只列举了前48位,当然我们待会在计算的时候实际上也只需要用到它的前48位,思路和我们上一篇文章是相同的。同样的,我们打开outputs2和outputs3也可以在同样的位置获得第二个LFSR和第三个LFSR各自的独立的输出流。
获取到各自独立的输出流之后,此时,这道题就成功的退化为了我们上一篇文章中讲的常规LFSR模型,因此只要按照上一篇文章的实现方法,分别求出各自的init,然后按照我们这道题目的要求拼接起来并计算哈希值,即为我们这道题目的flag,脚本如下:
from Crypto.Util.number import long_to_bytes
import hashlib
mask1 = '100000000000000000000000010000000000000000000000'
mask2 = '100000000000000000000000000000000010000000000000'
mask3 = '100000100000000000000000000000000000000000000000'
key1 = '100100011111111010101110010010110100101000110011'
key2 = '001101101101101111001001101101110000001001000011'
key3 = '001000101001101100100001101111101011101010100001'
tmp1=key1
tmp2=key2
tmp3=key3
init1 = ''
for i in range(48):
output = '?' + key1[:47]
ans = int(tmp1[-1-i])^int(output[-23])
init1 += str(ans)
key1 = str(ans) + key1[:47]
init1 = long_to_bytes(int(init1[::-1],2))
init2 = ''
for i in range(48):
output = '?' + key2[:47]
ans = int(tmp2[-1-i])^int(output[-14])
init2 += str(ans)
key2 = str(ans) + key2[:47]
init2 = long_to_bytes(int(init2[::-1],2))
init3 = ''
for i in range(48):
output = '?' + key3[:47]
ans = int(tmp3[-1-i])^int(output[-42])
init3 += str(ans)
key3 = str(ans) + key3[:47]
init3 = long_to_bytes(int(init3[::-1],2))
flag="flag{"+hashlib.sha256(init1+init2+init3).hexdigest()+"}"
print flag
执行一下脚本就可以得到我们这道题目的flag:
flag{b527e2621131134ec22250cfbca75e8c9f5ae4f40370871fd55910927f66a1b4}
这样来看的话,这道题目其实还是具有一定的难度的,但是在当时比赛时,这道题目其实是被相当多的战队攻克的,那么是什么原因造成的呢?其实,在当时比赛时,大部分战队并没有采用代数攻击的方式,而是直接使用了更为简易的z3约束求解的方式来解决这道题目的,接下来我们把这种做法也来讲解一下(注意:这种做法对我们国际赛上遇到的大部分题目其实都是行不通的,这里只是这道题恰巧满足了约束求解的条件,在我们比赛当中时,尝试使用z3约束来解题是一个不错的思路,鼓励大家尝试一下,但是大家也必须清楚这么解的话解不出来也是正常的,还是要在平时多点一些自己的代数攻击方面的技能点)。
z3约约束求解的核心思路其实很简单,就是列方程和解方程,只要你方程列对了,如果能解,z3就会给你一组解(注意:如果方程有多组解,z3只会给你其中的一组解,所以这组解虽然满足题意但未必是正确答案,这个时候我们可以尝试能否继续为方程添加约束条件,进一步限制解的范围,从而获得我们预期的一组解)。
那么我们接下来说一下这种z3的solver脚本如何来写,首先和方程一样,先要设未知数,我们要求解什么就把什么设成未知数,在z3我们一般常用两种,一种是Int,一种是BitVec,我们在求解LFSR时候一般用到的都是BitVec,比如这里我们要求的init1是一个48位的数,我们现在想要求它,就可以用下面这种写法把他设为未知数:
init1 = BitVec('init1', 48)
init2和init3的设法也是类似的,设完之后我们就要列方程,列方程就是我们已经知道这些变量满足哪些表达式了,我们就给他加进方程组里,这里我们的写法格式如下:
s = Solver()
s.add(outputs[i] == combine(l1.next(), l2.next(), l3.next()))
思路很简单,首先初始化一个Solver,大家可以把他理解为一个方程组,一开始刚一初始化完方程组是空的,需要我们往里面添加方程,s.add()里面写的就是我们这道题我们已知的表达式,和我们前面分析的过程是完全一样的,因此我们可以很容易的用z3把我们题目中的3个init解出来,代码如下:
#!/usr/bin/env python2
from z3 import *
class lfsr():
def __init__(self, init, mask, length):
self.init = init
self.mask = mask
self.lengthmask = 2**(length+1)-1
self.length = length
def next(self):
nextdata = (self.init << 1) & self.lengthmask
i = self.init & self.mask & self.lengthmask
output = 0
for j in range(self.length):
output ^= (i & 1)
i = i >> 1
nextdata ^= output
self.init = nextdata
return output
def combine(x1,x2,x3):
return (x1*x2)^(x2*x3)^(x1*x3)
init1 = BitVec('init1', 48)
init2 = BitVec('init2', 48)
init3 = BitVec('init3', 48)
l1 = lfsr(init1, 0b100000000000000000000000010000000000000000000000, 48)
l2 = lfsr(init2, 0b100000000000000000000000000000000010000000000000, 48)
l3 = lfsr(init3, 0b100000100000000000000000000000000000000000000000, 48)
s = Solver()
with codecs.open('keystream', 'rb', 'utf8') as f:
keystream = f.read()
outputs = []
for i in keystream:
a = ord(i)
b = '0'*(8 - len(bin(a)[2:])) + bin(a)[2:]
for j in b:
outputs.append(int(j))
for i in range(200):
s.add(outputs[i] == combine(l1.next(), l2.next(), l3.next()))
s.check()
print(s.model())
这里我们可以发现在最下面为Solver添加方程的时候,只添加了200个方程,按理来讲,我们应该有len(outputs)个方程,为什么只添加200个呢?实际上在这里200并不是一个精确数字,而是一个大概的数字,意思是当添加够200个方程的时候,得到的解就已经固定了,即我们需要的那组解,我们把它改到300,得到的还是这组解,所以就不用继续添加没有必要的方程了。那么既然我们说反正都一样,我直接给他添加len(outputs)个方程,不是更省事吗,也不用去关它多少个方程之后解就固定了,其实大家可以动手去试一下,这样虽然理论上是一样的,但是实际操作的时候计算机反而解不出来,原因就是约束的方程过多了,计算机反而解不出来了,因此我们需要手动测试一下,找到一个合适的数值,来使得我们的脚本既能求出我们希望的一组解,又能让计算机正常跑出来。
另外在class lfsr()这里,我们并不是原封不动的复制了题目当中的实现,还是做了一个细微的修改的,细心观察一下就会发现我们的这个LFSR类的实现在初始化这里多加了一行self.length = length,而题目原本的实现中是没有这一行的,为什么要做这样一个处理呢?原因就在于题目原本的实现中,在next()里是用while i != 0:来控制循环的,而i = self.init & self.mask & self.lengthmask,在我们z3版的solver当中,init是以未知数形式传进去的,没办法通过运算去变成一个具体数继而和0去比较来判断是否终止循环,因此我们在中需要换一个等价的写法,就是直接给他改成具体的次数,这个次数和i通过不停运算变成0的次数是相等的,即我们在初始化时候传入的最后一个参数length的值,因此我们直接循环length次,就解决了这一问题。
讲完了两种解法之后,实际上在写solver的时候在文件处理上还有一个小插曲,在这里也给大家讲一下:
在代码的最后部分我们可以很清楚的看到,程序执行了8192次循环,每次循环写入1个字节,因此最后keystream大小应该是8192字节才对,但是我们打开题目给出的keystream文件自己尝试一下就会发现我们得到的文件大小是11990而不是8192:
>>> with open('keystream','rb') as f:
... data = f.read()
...
>>> len(data)
11990
之所以会出现这样的情况,是因为我们每次在向文件中写入时,不是向上一篇文章中那样采用f.write(chr(b))来写的,而是使用了f.write(chr(b).encode())来写的,即多了一个encode()的操作,而就是多出来的这个操作造成了我们自己计算出来的长度不一致。这里我举一个例子来帮大家搞清楚这个问题,我们来观察下列操作和结果:
#python2下执行
>>> chr(127).encode()
'x7f'
>>> chr(128).encode()
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
UnicodeDecodeError: 'ascii' codec can't decode byte 0x80 in position 0: ordinal not in range(128)
#python3下执行
>>> chr(127).encode()
b'x7f'
>>> chr(128).encode()
b'xc2x80'
看到这里相信大家应该很清楚了,在python2下,当使用chr().encode()操作大于127的数字时,程序会报错;而在python3下,程序并不会报错,而是会采用2个字节的形式进行表示;但是当数字小于等于127时,在python2和python3下都可以正常的使用1个字节来表示。我们这道题目,实际上正是在python3下进行了这样的操作,导致在向文件写入时一会写入一个字节一会写入两个字节,从而出现了执行了8192次写操作但却写入了11990字节这一情况,那么我们如何将文件恢复成8192个字节的形式呢?
以128为例,我们实际上是希望向文件中写入1字节的x80,而不是写入2字节的xc2x80,那么实际上这里有如下的规则:
#在区间[128,192)内,数字的表示形式会加上xc2的前缀,例:
>>> chr(128).encode()
b'xc2x80'
#在区间[192,255)内,数字的表示形式会加上xc3的前缀,同时数字本身减去64,例:
>>> chr(192).encode()
b'xc3x80'
懂得了原因,我们就可以写一个脚本来讲题目中给出的11990字节的文件替换成可供我们使用的8192字节的文件了:
#!/usr/bin/python3
b = b''
with open('keystream','rb') as f:
data = f.read()
i = 0
while i < len(data):
if data[i] == 194:
b += bytes([data[i+1]])
i += 1
elif data[i] == 195:
b += bytes([data[i+1] + 64])
i += 1
else:
b += bytes([data[i]])
i += 1
with open('new_keystream', 'wb') as f:
f.write(b)
或者直接采用更简单的办法:
#python3环境下
>>> with open('keystream','rb') as f:
... data = f.read()
...
>>> data = data.decode()
>>> len(data)
8192
当然python2下我们也可以采用相应的办法,按照我们的意愿来读取文件:
#python2环境下
>>> import codecs
>>> with codecs.open('keystream', 'rb', 'utf8') as f:
... data = f.read()
...
>>> len(data)
8192
总结
在本篇文章中,我们对LFSR类题目涉及到的一些数学/密码学知识进行了扩充,同时以0CTF的一道典型例题为例,介绍了代数攻击求解和z3约束求解两种解法,在后面的文章中,我们会进一步提升LFSR题目的难度,同时补充上对应的代数知识,感谢大家的阅读。
参考
https://ctf-wiki.github.io/ctf-wiki/crypto/streamcipher/fsr/intro/
https://link.springer.com/content/pdf/10.1007/978-3-642-21702-9_4.pdf
http://www.docin.com/p-560515320.html
http://zzs.ujs.edu.cn/xbzkb/CN/article/downloadArticleFile.do?attachType=PDF&id=1440


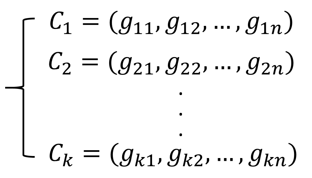
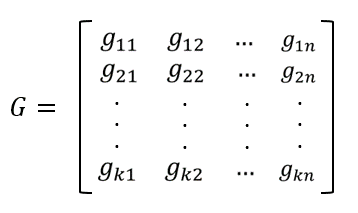
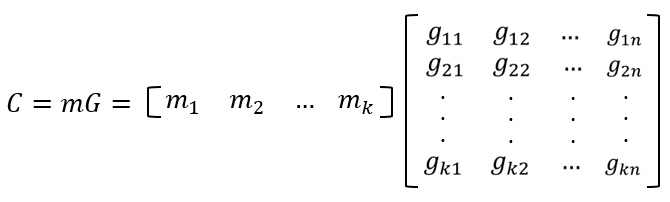
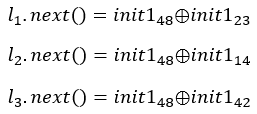
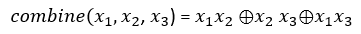
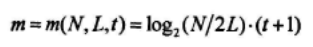
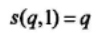
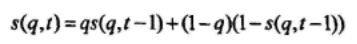
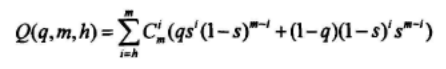
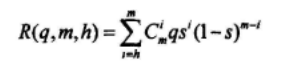
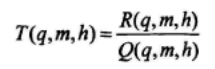
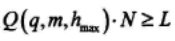
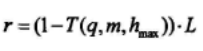
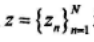
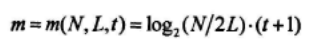
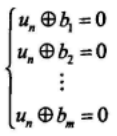
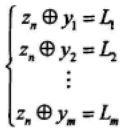
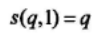
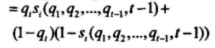
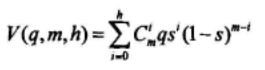
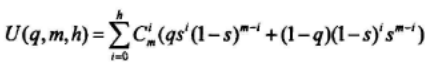
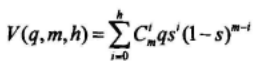
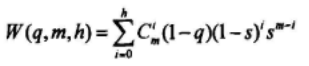
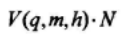
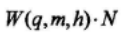
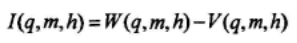
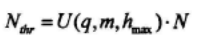







发表评论
您还未登录,请先登录。
登录