前言
在N1CTF 2019中有2道Crypto方向的题目,其中包含一些比较有意思的考点,在这里对题目进行一下分析。
BabyRSA
题目给出的python脚本如下:
#!/usr/bin/env python2
# -*- coding: utf-8 -*-
from Crypto.Util import number
import random
from secret import flag
N = 23981306327188221819291352455300124608114670714977979223022816906368788909398653961976023086718129607035805397846230124785550919468973090809881210560931396002918119995710297723411794214888622784232065592366390586879306041418300835178522354945438521139847806375923379136235993890801176301812907708937658277646761892297209069757559519399120988948212988924583632878840216559421398253025960456164998680766732013248599742397199862820924441357624187811402515396393385081892966284318521068948266144251848088067639941653475035145362236917008153460707675427945577597137822575880268720238301307972813226576071488632898694390629
e = 0x10001
m = number.bytes_to_long(flag)
with open('flag.enc', 'w') as f:
while m:
padding = random.randint(0, 2**1000) ** 2
message = padding << 1 + m % 2
cipher = pow(message, e, N)
f.write(hex(cipher)+'n')
m /= 2
可以看到,padding是由一个[0,2**1000]区间上的随机数r经过平方运算后得到的,即:
接下来,padding和m通过运算生成了message,这里需要注意一下运算符之间的优先级,即我们这里实际上是:
message = padding << (1 + m % 2)
而不是:
message = (padding << 1) + (m % 2)
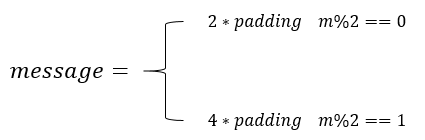
因此,当m%2==0,即m的最后一位为0时,message=padding<<1;当m%2==1,即m的最后一位为1时,message=padding<<2。即:
接下来,对message使用(e,N)公钥进行RSA加密,即:
最后,将加密结果写入flag.enc文件,并执行m/=2,即将m右移一位,并重复执行上述操作,直到对m的每一位都操作完毕。
将上述表达式整理一下,我们可以得到如下表达式:
将该表达式做一个变形,我们可以得到如下表达式:
之所以要变成这种形式,是为了引出接下来我们要讲的一个概念——雅可比符号(Jacobi symbol),在介绍雅克比符号前我们还是先讲一下勒让德符号(Legendre symbol),因为雅克比符号是作为勒让德符号的推广的形式出现的。
我们先来看一下勒让德符号的定义:
所谓二次剩余,是指当存在某个X,使得下述表达式成立,则称d是模p的二次剩余,否则称d是模p的非二次剩余。
接下来我们来看一下什么是雅克比符号:
通过定义我们不难发现,当上式中的m为奇素数时,雅克比符号就是勒让德符号。此时,我们有一条非常重要的推论:
但是显然,对于我们这道题目中的大整数N来讲,它并不是一个奇素数,而是一个奇合数,此时我们只能借助雅克比符号的推论来解决题目,但是对于雅克比符号来讲:
上面这条推论具有不确定性,但与此同时,雅克比符号也有下面这条确定性的推论:
接下来我们回过头来看一下之前变形后的cipher表达式,可以发现,当m==1时,该二次剩余方程显然有解(如(2*r)^e),而我们又知道,若jacobi(cipher,N)==-1,则方程一定无解,因此当jacobi(cipher,N)==-1时,m一定不会为1,因此此时m只能为0了。这样一来,当jacobi(cipher,N)!=-1时,此时m只能为1了。我们将该推理过程写成脚本如下:
#!/usr/bin/env python2
from gmpy2 import *
from libnum import *
N = 23981306327188221819291352455300124608114670714977979223022816906368788909398653961976023086718129607035805397846230124785550919468973090809881210560931396002918119995710297723411794214888622784232065592366390586879306041418300835178522354945438521139847806375923379136235993890801176301812907708937658277646761892297209069757559519399120988948212988924583632878840216559421398253025960456164998680766732013248599742397199862820924441357624187811402515396393385081892966284318521068948266144251848088067639941653475035145362236917008153460707675427945577597137822575880268720238301307972813226576071488632898694390629
e = 0x10001
f = open('flag.enc','rb').read().split()
cipher = [int(i,0) for i in f]
flag = ""
for i in cipher:
if jacobi(i,N)==-1:
flag += '0'
else:
flag += '1'
flag = int(flag[::-1],2)
print n2s(flag)
执行脚本即可得到flag:
N1CTF{You_can_leak_the_jacobi_symbol_from_RSA}
这里我们再拓展一下,如果我们这道题当中就是message = (padding << 1) + (m % 2)这种情况,那么还可以用这种思路来解吗。答案是可以的,我们来分析一下,这种情况下我们有:
此时,对于m==0这种情况,如果我们对cipher乘上一个invert(2**e,N),那么就又变成了一个二次剩余的问题,此时该二次剩余方程显然有解(如r^e),而我们又知道,若jacobi(cipher,N)==-1,则方程一定无解,因此当jacobi(cipher,N)==-1时,m一定不会为0,因此此时m只能为1了。这样一来,当jacobi(cipher,N)!=-1时,此时m只能为0了。我们将该推理过程写成脚本如下:
#!/usr/bin/env python2
from gmpy2 import *
from libnum import *
N = 23981306327188221819291352455300124608114670714977979223022816906368788909398653961976023086718129607035805397846230124785550919468973090809881210560931396002918119995710297723411794214888622784232065592366390586879306041418300835178522354945438521139847806375923379136235993890801176301812907708937658277646761892297209069757559519399120988948212988924583632878840216559421398253025960456164998680766732013248599742397199862820924441357624187811402515396393385081892966284318521068948266144251848088067639941653475035145362236917008153460707675427945577597137822575880268720238301307972813226576071488632898694390629
e = 0x10001
f = open('flag.enc','rb').read().split()
cipher = [int(i,0) for i in f]
flag = ""
for i in cipher:
if jacobi(i*invert(2**e,N),N)==-1:
flag += '1'
else:
flag += '0'
flag = int(flag[::-1],2)
print n2s(flag)
执行脚本同样可以得到flag。
Guess_ex
这道题是一道源码+服务器交互题,题目给出的python脚本如下:
#!/usr/bin/env python2
# -*- coding: utf-8 -*-
import sys, os, math, random, signal
def w(c):
sys.stdout.write(c)
sys.stdout.flush()
def wl(l):
w(l)
return w('n')
def ri(prompt):
try:
w(prompt)
ret = int(raw_input())
except:
sys.exit(1)
return ret
floor = lambda x: long(math.floor(x))
ceil = lambda x: long(math.ceil(x))
NTRIES = 10
P = 1180377880254925849184613297220733950775082607541
e = 0.05
r = 1.0
delta = P ** ((2 * r - 1) / 5 - e)
d = ceil(4 * (1 / e) / 5)
messup = lambda x: random.randint(x - floor(delta), x + floor(delta))
def main():
signal.alarm(90)
for _ in xrange(NTRIES):
a = random.randint(0, P - 1)
t = [random.randint(0, P - 1) for _ in xrange(d)]
u = [(a * x) % P for x in t]
A = messup(a)
T = map(messup, t)
S = map(messup, u)
wl(str(A))
wl(repr(T))
wl(repr(S))
answer = ri("Input number: ")
if answer != a:
wl("Wrong anwser!")
return 1
with open("/flag", 'rb') as f:
w(f.readline())
return 0
if __name__ == '__main__':
sys.exit(main())
梳理一下逻辑,可以发现我们的任务就是通过A、T和S这三个参数来恢复出a参数,那么我们就来看一下这几个参数之间有什么关系。
首先程序给定了几个固定参数:
P = 1180377880254925849184613297220733950775082607541
e = 0.05
r = 1.0
delta = P ** ((2 * r - 1) / 5 - e) #delta=16248121.55210456
d = ceil(4 * (1 / e) / 5) #d=16
接下来,a是一个在区间[0,P-1]上的随机数;t是一个长度为16的列表,每一个列表成员都是一个在区间[0,P-1]上的随机数;u是一个长度为16的列表,其每一个列表成员是由a乘以t的每一个列表成员再模P计算而来的。
随后我们看到,对a、t和s这三个参数的所有成员应用messup函数,就得到了A、T和S这三个参数,而messup函数会生成一个区间[x-16248121,x+16248121]上的随机数(x为传入messup的函数)。
换句话说,我们实际上有如下表达式:
如果我们能求出ea,也就意味着我们能够求出a了,鉴于这里的ea、et和es都是很小的整数,我们可以将其设为未知数,然后采用解方程组的思想来求出它们的值,我们可以采用如下方法来构造方程组:
我们可以这样来理解这个方程组:
其系数矩阵第一行为:
其系数矩阵第二行为:
以此类推,最终我们可以构造出一个16*50的系数矩阵,那么我们去解系数矩阵*X=O这样一个方程,如果能够得到一个50*1的矩阵,那么很大程度上就是我们需要的解了,其中第17行的元素即我们需要的ea。
我们尝试构造这样一个系数矩阵,并尝试使用SageMath下的right_kernel_matrix来求解。
M = []
for i, (ti, si) in enumerate(zip(T, S)):
lpadding = [0] * i
rpadding = [0] * (d - i - 1)
yi = (A * ti - si) % P
row = lpadding + [A] + rpadding + [ti] + lpadding + [1] + rpadding + lpadding + [P] + rpadding + [yi]
M.append(row)
M = Matrix(M)
k = M.right_kernel_matrix()
k = k.transpose()
但是当我们查看k时,却发现得到的是一个50*34的矩阵,而不是我们预期的50*1的矩阵:
sage: k
50 x 34 dense matrix over Integer Ring (use the '.str()' method to see the entries)
那么如何将这个形式的矩阵转化成我们需要的矩阵呢,这里就需要用到格基规约的思想,也就是我们经常在CTF中用到的LLL算法。
所谓LLL算法,就是在格上找到一组基,满足如下效果:
回到我们这道题上,实际上就是在解决一个SIS(Short integer solution)问题:
在SageMath当中,也集成了LLL这一方法,我们只需要调用:
k = k.LLL()
k = k.transpose()
然后得到的新的矩阵的第一列,即为我们预期得到的方程组的一组解,根据我们构造的系数矩阵,k[16][0]即为我们需要的ea,我们可以写一个POC来验证一下:
import sys, os, math, random, signal
floor = lambda x: long(math.floor(x))
ceil = lambda x: long(math.ceil(x))
P = 1180377880254925849184613297220733950775082607541
e = 0.05
r = 1.0
delta = P ** ((2 * r - 1) / 5 - e)
d = ceil(4 * (1 / e) / 5)
messup = lambda x: random.randint(x - floor(delta), x + floor(delta))
a = random.randint(0, P - 1)
t = [random.randint(0, P - 1) for _ in xrange(d)]
u = [(a * x) % P for x in t]
A = messup(a)
T = map(messup, t)
S = map(messup, u)
M = []
for i, (ti, si) in enumerate(zip(T, S)):
lpadding = [0] * i
rpadding = [0] * (d - i - 1)
yi = (A * ti - si) % P
row = lpadding + [A] + rpadding + [ti] + lpadding + [1] + rpadding + lpadding + [P] + rpadding + [yi]
M.append(row)
M = Matrix(M)
k = M.right_kernel_matrix()
k = k.LLL()
k = k.transpose()
if k[49][0]==-1:
ea = k[16][0]
else:
ea = -k[16][0]
A==a+ea
执行这段代码,我们可以看到程序的返回结果为True,说明我们的方法是可行的,那么接下来,我们只需要用我们在nc连接中得到的A、T和S来替换POC中随机生成的A、T和S,然后将A-ea的值发送到服务器,即可得到flag,最后flag如下:
N1CTF{4751c6182fea7490dadf384db308becc}
参考
https://en.wikipedia.org/wiki/Short_integer_solution_problem
https://www.davidwong.fr/papers/david_wong_rsa_lll_boneh_durfee__2015.pdf


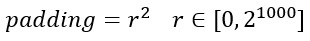
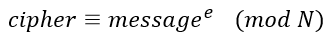
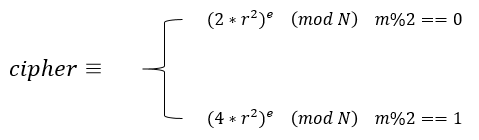
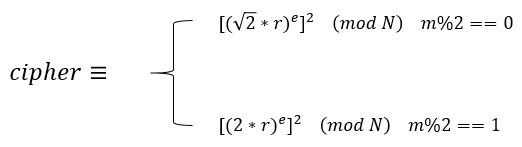

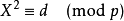
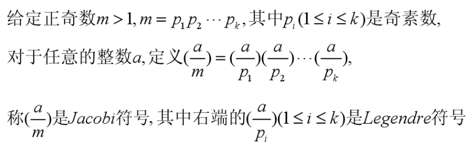
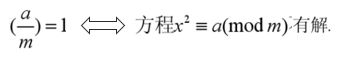
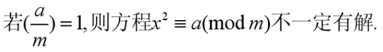
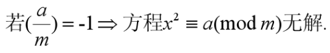
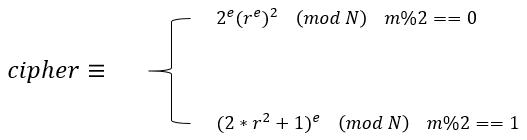
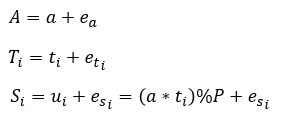
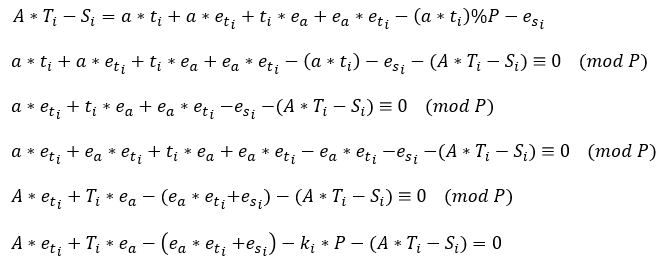
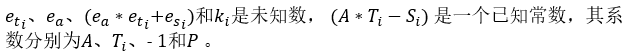
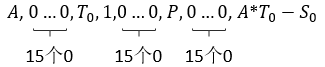
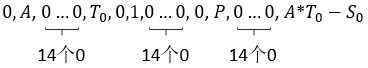
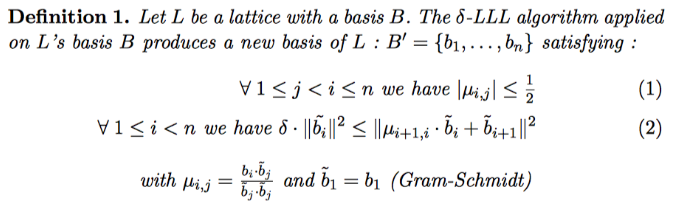








发表评论
您还未登录,请先登录。
登录