作者:唐银@涂鸦智能安全实验室
一、前言
本文从阅读难度上可以划分为两个部分,一、二、三、四、六小节算是一部分,主要是原理性的叙述讲解,五算是另外一个部分,内容是详细的数学推导过程。
阅读第一部分之前你只需要了解什么是向量、向量的转置、什么是矩阵,也就是线性代数的基本常识。第二部分对读者的数学基础要求稍微高了一点,你需要了解概率论、微积分、凸优化相关的知识。
首先声明,本文没有算法和理论上的创新,可能不能让AI安全大佬满意。当然,如果大佬能在百忙之中给予一些指导,笔者将感激不尽!
如果你对AI安全感兴趣,并且想要搞清楚背后的原理,那么这篇文章就是为你写的。在没有搞清楚原理之前,你可能觉得机器学习用在安全问题上就是门玄学技术(信则有,不信则无的那种)。希望阅读完之后,能够改变你的看法,并且帮助你把这门“玄学”技术应用到实际的工作问题中。
初次了解到隐马尔可夫模型在Web安全异常检测领域的应用是几年前,一次偶然的机会读到楚安的文章《数据科学在Web威胁感知中的应用》。前前后后也花了很多精力去学习机器学习相关的理论,当看到各种精妙的数学推导时,深深感受到了人与人之间智商上的鸿沟,惊叹于前人智慧的同时,也体验到了求知的乐趣。最近恰好工作需要,有机会重新捡起这些知识,发现细节都忘的差不多了,于是重新梳理了一遍,把内容整理下来,希望能够帮助到更多的人,在求知的道路上节省一些时间。
传统的入侵检测技术通常是基于规则的,类似黑名单的方式去匹配哪些流量是恶意的攻击,而黑客经常可以找到新的绕过方法。作为防守方,面对复杂的业务,如果规则上追求通用性,要么防护效果无法达到预期,要么产生很多误报,而基于这样的规则进行拦截,甚至可能会影响到正常的业务运行。如果规则上追求更强的针对性,那么维护成本也会增大。
近些年,各种机器学习算法不断被应用于Web安全入侵检测领域,与传统的入侵检测技术形成互补。隐马尔可夫算法是其中比较有代表性的一个,原理主要是基于大量的正常流量数据训练模型,利用模型检测新的流量数据,当流量数据与模型不符时,判定为异常流量。这种方式类似于白名单,更难绕过,但与白名单规则不同的是,机器学习模型具有更好的泛化能力,即使两条正常流量中数据内容完全不同,依然可以达到很好的识别能力。
二、从玩骰子开始
假设有三个不同的骰子(Dice)。
第一个是一个四面体的骰子,每个面的数字分别是1到4,各个面出现的概率相等,都是1/4。(给这个骰子起个名字叫D4)
第二个是正常骰子,6个面,每个面出现的概率相等,都是1/6。(这个骰子叫D6)
第三个是一个八面体的骰子,每个面的数字分别是1到8,各个面出现的概率相等,为1/8。(这个骰子叫D8)
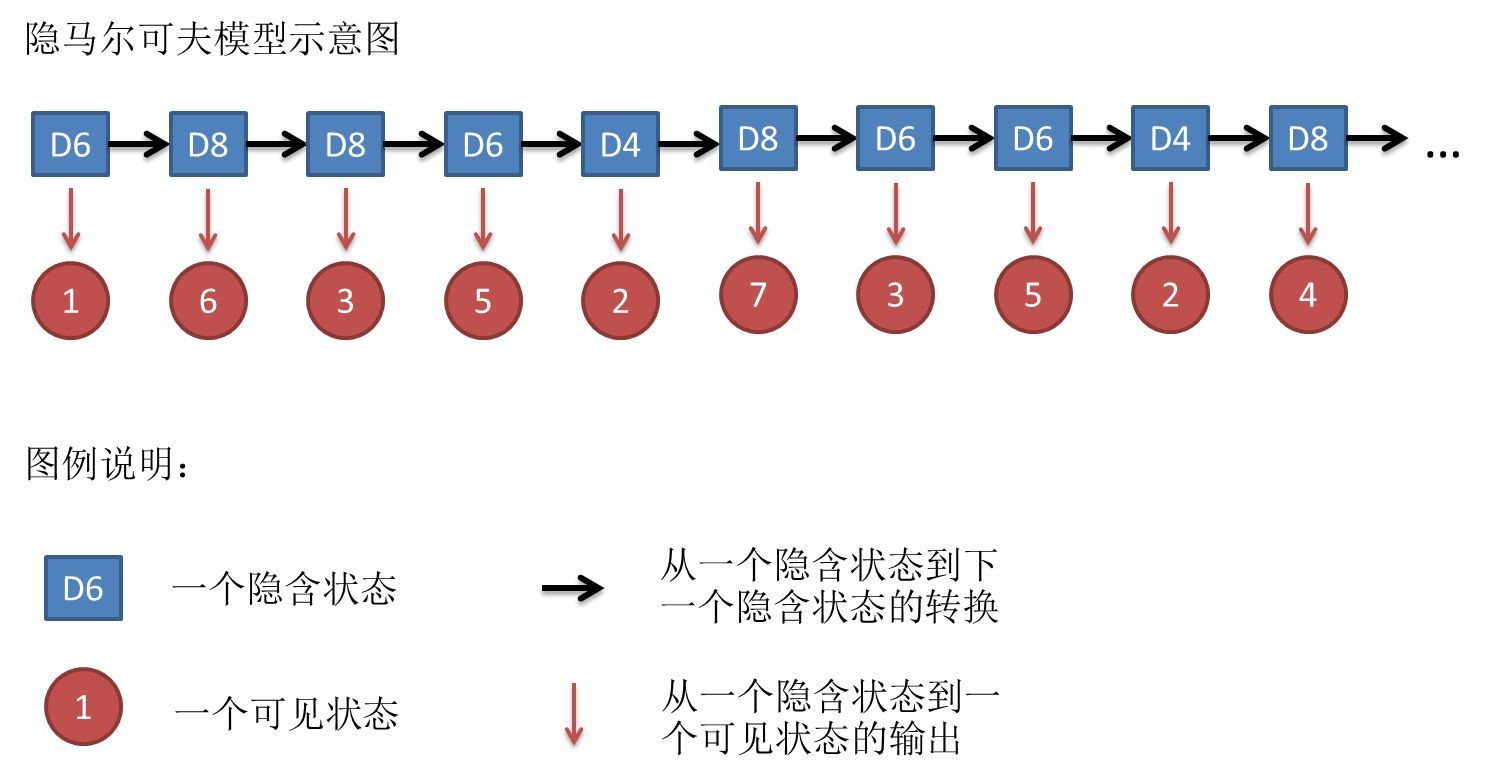
现在我从三个骰子里随机挑一个,假设拿到每个骰子的概率都是1/3,抛一下骰子,得到一个数字。重复循环这个过程,重复了10次,得到了一串数字 1 6 3 5 2 7 3 5 2 4。
假设我不告诉你我每次挑到的是哪个骰子,只把这串数字告诉你,相当于你只是观测到了这串数字。那么对于你来说,这串可观测到的数字连在一起就是观测序列。
而我每次挑到的是哪种骰子,对你来说是隐含的状态,把这些隐含状态记录连起来,就是隐含状态序列。比如说,这个隐含状态序列可能是D6、D8、D8、D6、D4、D8、D6、D6、D4、D8 。
到这里,我们可以通过类比去理解几个概念:
1、状态集合
三种骰子分别对应三种不同状态,这里状态集合就是:Q = {D4,D6,D8}
2、观测集合
骰子的数字对应所有可以观测到的结果,这里观测集合就是:V={1,2,3,4,5,6,7,8}
3、隐含状态序列
Z = {D6,D8,D8,D6,D4,D8,D6,D6,D4,D8}
4、状态序列和观测序列的长度
前面我们重复了10次实验,所以状态序列和观测序列的长度就是:T=10
5、初始状态概率分布
我们假设第一次(注意这里说的是第一次)三个骰子被取到的概率都是1/3,那么可以用向量的形式表示:
对于骰子问题,这个就是其对应的初始状态概率分布。
6、状态转移概率(transition probability)分布
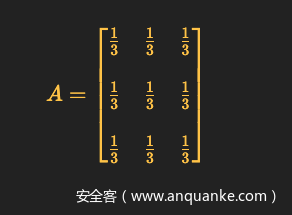
也叫状态转移矩阵,先给出来再解释
第一行第一列,表示本次隐含状态是D4,下一次还是D4的概率;
第一行第二列,表示本次隐含状态是D4,下一次是D6的概率;
第二行第一列,表示本次隐含状态是D6,下一次是D4的概率;
······
以此类推。
这个是按照最开始我们的假设,每次选择骰子都是随机等概率的,所以状态转移矩阵里每一项状态转移概率值都一样。
现在我们更改一下状态转移的假设:
如果取到的骰子是D4,那么下一个只能取D8;如果取到D8,下一个取到D4的概率是0.2,取到D6的概率是0.7,再次取到D8的概率是0.1;如果取到D6,下一个取到D4和D8的概率都是0.5,不能连续取D6。
那么对应上述条件的状态转移矩阵就是:
7、输出概率(emission probability)分布
隐含状态到可见状态之间的概率叫输出概率,也叫发射概率。
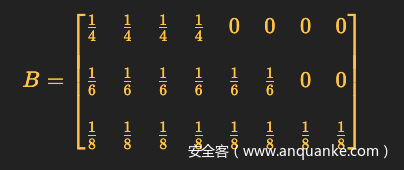
按照最初假设的骰子规则,对应的输出概率分布:
每行分别对应D4、D6、D8三个骰子抛出后出现数字1-8的概率。
假设我出千,D6被我做了手脚,抛出6的概率是1/2,其余数字都是1/10,那么对应的输出概率分布为:
三、隐马尔可夫模型的三个基本问题
我们用数学符号来抽象表示一下上面的模型:θ=(A,B,π)
θ用来表示模型
A表示状态转移矩阵
B表示输出概率分布
π表示初始状态概率分布
概率计算问题(评估问题)
仍然以最初的骰子问题为例,已知模型:θ=(A,B,π)
其中,状态转移矩阵:
输出概率分布:
初始状态概率分布:
已知观测序列:Y=(1,6,3,5,2,7,3,5,2,4)
求在上述模型θ下观测序列Y出现的概率P(Y∣θ)。
相当于你知道骰子有几种(状态集合),每种骰子是什么样的(状态转移矩阵),根据骰子抛出的结果(观测序列),你可以计算抛出这个结果的概率。
看到这里,你可能会问,我是谁?我在哪?我为啥要算这玩意???
既然你能抛出这一串结果,那么说明这一串结果的出现的概率是比较大的。你计算一下在当前已知模型下出现这一串序列的概率,如果得到的概率非常非常小,你基本可以判断,我出千了,我用的骰子不符合正常骰子的模型。如果是正常的模型θ,不太可能会出现这一串数字。换个角度看,这一串数字对于正常模型来说,就是异常情况!
总结起来就是,你可以用观测序列评估模型是否靠谱;也可以假设模型是靠谱的,用这个模型来评估观测到的数据是否异常。
学习问题
已知有3种骰子,已知观测序列Y = (1,6,3,5,2,7,3,5,2,4)。估计模型θ=(A,B,π)的参数,使得以估计出来的参数作为前提条件时,出现这个观测序列的概率P(Y∣θ)最大。
相当于,你现在知道有几种骰子(但是不知道都是啥样的骰子),还知道骰子抛出来的结果(观测序列),其他就啥也不知道了。现在让你掐指算一下,骰子都是啥样的,A,B,π里面的值都得求出来。
看到这,你应该又是一脸问号,what?我就知道这么点信息,这能算出来?鲁豫看了都想说:
当我第一次看到这个问题的时候,我也不信,后面算完我就相信了。
预测问题(解码问题)
已知模型θ=(A,B,π),已知观测序列Y = (1,6,3,5,2,7,3,5,2,4),求最有可能对应的隐含状态序列Z,也就是计算概率P=(Z∣Y,θ),得到能让这个概率最大的Z。
相当于,你知道骰子有几种(状态集合),每种骰子是什么样的(状态转移矩阵),根据骰子抛出的结果(观测序列),可以计算出每次抛的是哪种骰子(隐含状态序列)。
四、对应到Web请求参数异常检测中
对于上面三个问题,我会在后面讲具体怎么求解。为了防止数学计算/公式导致的劝退现象,我打算先提前讲一下隐马尔可夫模型为什么可以用在Web安全相关的参数异常检测中,以及和上述基本问题的对应关系。
“正常总是基本相似,异常却各有各的异常。“基于这样的假设前提,隐马尔可夫模型才可能达到比较好的效果。也就是说,隐马尔可夫模型只适用于正常请求参数都比较相似的场景。
概率计算问题(评估问题)
假设有一个填写用户邮箱功能的Web Api,下面是3条业务中产生的正常post请求数据:
{"id":"12334", "email": "zhangsan@xx.com"}
{"id":"14352", "email": "lisi@xx.com"}
{"id":"27988", "email": "wangwu@xx.com"}
下面是三条攻击者发送的异常请求数据:
{"id":"67123' union select 1,2,3", "email": "asdf@xx.com"}
{"id":"67123", "email": "asdf@xx.com\\"\>\<img src=1 onerror=alert('xss')\>"}
{"id":"67123", "email": "asdf@xx.com' and 1=1-- a"}
可以看到上面正常的请求中,参数值都是比较相似的。而攻击请求的Payload和正常参数值有很大不同。如果我们能够利用大量的正常请求参数,通过计算学习到一个模型,再拿这个模型去评估新的数据,那么不符合这个模型的数据,都可以判定为异常。
现在,你可以想象每个请求参数对应着一套形状各不相同的不规则骰子,每个骰子都有很多面,每个面上刻着一个字符。这一套骰子以及每次抛之前选骰子的规则加在一起就是我们的模型。有了这个模型,每次你就可以对新输入的字符串进行计算,如果是正常请求的参数字符串,这套骰子能把它抛出来的概率一定远大于异常请求参数被抛出来的概率。
例如:id这套骰子,只能抛出来数字,如果你看到其他字符出现在结果里,那肯定不是这套骰子抛出来的。同样email这套骰子能抛出来的字符也有限,除了字母就是@.这两个符号,如果结果里出现尖括号<,那也不会是这套骰子抛出来的。对于异常的情况,在模型下的条件概率会非常非常小,甚至为0。
学习问题
要根据上面的理论通过计算区分正常和异常,前提条件是,我们得先有一个Web请求参数的模型,那么该如何得到这个模型呢?
继续想象每个请求参数对应着一套形状不规则的骰子,每个骰子有多少面以及形状是否规则(决定输出概率)我们是不知道的,每次抛骰子前如何选骰子的规则我们也不知道(决定状态转移矩阵),第一次应该选哪个骰子来抛我们也不知道(决定初始状态概率分布)。
我们唯一知道的,就是一堆观察到的字符串,也就是这套骰子每次抛出来的结果。
如果能反推出来上面所有的未知信息,那么我们就成功得到了模型。
接下来我们尝试建立模型。
从Web安全的角度看,数字、字母、汉字、其他语言类型的字符与一些特殊字符对于参数注入类型的攻击Payload类型来说,有着明显意义上的不同。如果我们把每个观测到的字符都直接加入观测集合,那么将会导致我们的模型非常复杂,模型越复杂,泛化能力就可能越差。(想象一下,需要大量的骰子,每个骰子有特别多的面,才能表示出模型,直觉上计算量和预测效果都不会太理想。)
所以,我们可以将数字、字母等字符用统一的符号代替。比如数字用N(Number)、字母、汉字、其他语言类型的字符用A(Alphabet)来表示,特殊字符可以不做转化处理直接表示观测状态,加入观测集合。
例如,
{"id":"12334", "email": "zhangsan@xx.com"}
这条数据用上面的方法表示成观测序列就是:
{"id":"NNNNN", "email": "AAAAAAAA@AA.AAA"}
接下来对比上一个小节讲的学习问题,可以看到,那里除了观测到的骰子序列,还有一个已知条件——骰子个数为3。而这里我们是不知道一个Web请求参数应该对应几个骰子(隐含状态)的,那怎么办呢?
那就只能靠假设了,问题又来了,假设有多少个合理呢?如果你了解过机器学习,那么你应该大概率听说过“调参侠”,这是机器学习工程师对自己工作自嘲的称谓。在机器学习领域,很多参数是要人工去尝试着调节的(在我们的上下文中,这里的参数指隐含状态的个数)。很多问题,目前为止都没有严谨的数学算法能够通过计算调节出最优的参数,遍历所有的数字去计算也不现实,毕竟目前人类社会科技的发展阶段还不支持这样的算力。我们只能退而求其次,通过有限次数的调节,最终去寻找一个相对更优的参数。
在《数据科学在Web威胁感知中的应用》这篇文章里,作者取了所有观测序列中的观测状态数均值做了四舍五入作为隐藏状态数。
对于这种选取方式的合理性暂时不做探讨,因为在没有找到足够的理论依据,以及足够量级的实践之前,笔者也不好妄下结论。可以先完全照搬,以此为起点,在前人的经验上继续探索。
再比如,这两篇语音识别问题相关的论文中,隐藏状态数选取在6~8之间:
《语音识别中隐马尔可夫模型状态数的选取原则及研究》
《语音识别中隐马尔可夫模型状态数的研究》
虽然问题不同,但理论上也许可以借鉴,或许能找到更好的隐藏状态数选取方式。
预测问题(解码问题)
这个问题其实和我们要做的Web请求参数异常检测没什么关系。主要用在翻译,语音识别等问题上。比如根据训练好的模型,用一段观测到的音频序列,预测出其代表的文字(隐藏状态)。由于我们的问题用不到,所以这个就不做过多解释了,感兴趣的读者可以自行探索。
如果可以求解前两个基本问题,那么就可以说明隐马尔可夫模型用到Web安全参数异常检测问题上是有完整的理论依据的,等你搞清楚这个理论依据,这个问题就不再是个玄学问题了。
五、求解
数学警告!如果感觉看不下去,记住结论就好,上面讲的,真的是可以算出来的!如果对这部分感兴趣,就请继续往下看。
要读懂下面的内容,你需要了解概率论、微积分、凸优化相关的知识。
学习问题
如何推导学习问题呢?这里要用到EM(Expectation Maximization,期望极大)算法。
先复习一下Jensen不等式,后面会用到。如果不了解或者忘记了,可以先看下笔者以前写的关于凸优化的笔记《凸优化相关概念整理总结》。
Jensen不等式:
在隐马尔可夫模型的参数学习问题中,假设我们用Y表示观测变量的数据,Z表示隐含变量的数据,θ表示需要估计的模型参数。
我们面对的是一个含有隐含变量Z的概率模型,目标是极大化观测数据Y关于参数θ的对数似然函数,即极大化:
这一极大化求解的重要困难是:上面式子中有未观测数据(隐含变量)Z,有包含和(Z为离散型时)或积分(Z为连续型时)的对数,很难通过求导等于0求得解析解。
EM算法采用的是通过迭代逐步近似极大化L(θ):
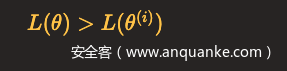
假设在第i次迭代后θ的估计值是θ(i),我们希望新的估计值θ能使L(θ)增加,即
并逐步达到极大值。为此,考虑两者的差:
由于ln(x)是凹函数,且
把
看作一个整体。那么可以根据Jensen不等式,得到
所以
所以
令
则
注意,这里θ(i)是已知的,我们在前面讲过,这是第i次迭代后的参数值。对于一个学习问题,我们通常会初始化参数值,作为第一次迭代的输入参数值。
由于θ(i)是已知的,所以上式不等号两边都是关于θ的函数。
函数B(θ,θ(i))是L(θ)的一个下界,假设θ(i+1)可以使得B(θ,θ(i))达到极大,即
那么
因此,任何可以使B(θ,θ(i))增大的θ,也可以使L(θ)增大,于是问题就转化为了求解能使得B(θ,θ(i))达到极大的θ(i+1),即
省去对θ最大化而言是常数(不影响计算)的项,
令
至此,我们成功把求不完全数据Y(观测数据Y也称不完全数据)的对数似然函数L(θ)=lnP(Y∣θ)极大化问题转化为了求:完全数据(观测数据Y和隐含状态Z连在一起称为完全数据)的对数似然函数L(θ)=lnP(Y,Z∣θ)关于在给定观测数据Y和当前参数θ下对未观测数据Z的条件概率分布P(Z∣Y,θ(i))的期望,也就是Q函数。
EM算法中的E(Expectation)指的就是上述步骤。而M(Maximization)指的就是求Q函数的极大值,这个极大值是可以通过求导的方式计算得到的。
推导完EM算法,我们现在回过头再看隐马尔可夫模型,将模型的学习问题代入EM算法。
将观测数据记做
隐含状态序列记做
完全数据是
用
EM算法E步:求Q函数
省去常数因子,则
于是
EM算法M步:极大化Q函数,求模型参数A,B,π
对于上式,可以对相加的各项分别极大化。第一项
这里N代表隐含状态总数,由于
所以可以用拉格朗日乘子法,写出拉格朗日函数:
上式对π_i求偏导数并令结果为0,解得
代回上面等式,得
Q函数第二项
状态转移概率矩阵中每一行的元素之和为1,所以可以利用具有约束条件的拉格朗日乘子法,这里N代表隐含状态总数。
对a_ij求偏导,令结果等于0,得到
带回上面式子,得到
Q函数最后一项:
每种状态的发射概率之和为1,同样利用拉格朗日乘子法,这里M表示观测集合元素总数,v_k表示观测状态。
对b_j(y_t)求偏导,令结果等于0,得到
对b_j(v_k)求偏导,令结果等于0,只有当y_t = v_k时,b_j(y_t)对b_j(v_k)的偏导数不为0,用I(y_t = v_k)表示该偏导数,可以得到
呼~终于把学习问题推导完了。
概率计算问题(评估问题)
上述学习问题中的各项结果具体的计算,以及已知模型时,计算当前观测序列由已知模型生成的概率,都要用到概率计算问题中的前向-后向算法。算法比较简单,容易理解,这里就不再展开赘述了,感兴趣的读者可以查阅文章末尾的参考资料去了解。
上面这些内容,只是证明了可以通过计算,利用输入的训练数据(观测序列)得到可用的模型,再利用得到的模型可以反过来评估输入数据是否符合模型。
从头到尾完整推导下来,我们就可以很清晰的理解隐马尔可夫模型应用于Web参数异常检测的合理性了。
六、其他
开篇骰子的例子参考了《白话大数据和机器学习》中的示例,这个示例是我看过的几个讲解隐马尔可夫模型的示例中相对比较好的一个,所以选择了用这个示例来类比Web安全相关的参数异常检测问题。
由于参考了很多不同的资料,每份资料的数学公式符号和推导过程都略有不同,笔者在写作过程中尽量将符号统一以增强连贯性,便于理解。
后面如果有时间,打算再接着写一篇实践相关的文章,谈谈HMM算法在大数据实时计算场景下的具体实现以及架构设计。
行文仓促,为了更直白的说明问题,帮助读者理解,一些表述也许并不严谨。且推导过程对于严谨性的要求较高,难免出错。如有错误,欢迎指正。
参考资料:
《统计学习方法》
《白话大数据与机器学习》
《数据科学在Web威胁感知中的应用》
《基于机器学习的web异常检测》
《语音识别中隐马尔可夫模型状态数的选取原则及研究》
《语音识别中隐马尔可夫模型状态数的研究》
知乎:如何用简单易懂的例子解释隐马尔可夫模型?
徐亦达机器学习:Hidden Markov Model 隐马尔可夫模型(HMM)
漏洞悬赏计划:涂鸦智能安全响应中心( https://src.tuya.com )欢迎白帽子来探索。
招聘内推计划:涵盖安全开发、安全测试、代码审计、安全合规等所有方面的岗位,简历投递sec#tuya.com,请注明来源。









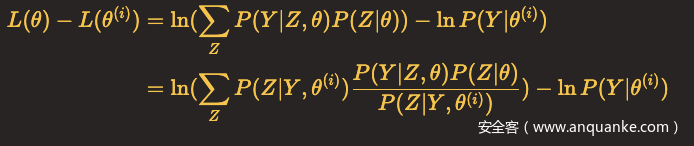


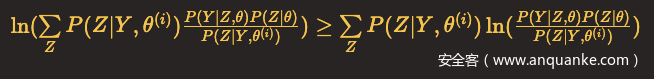
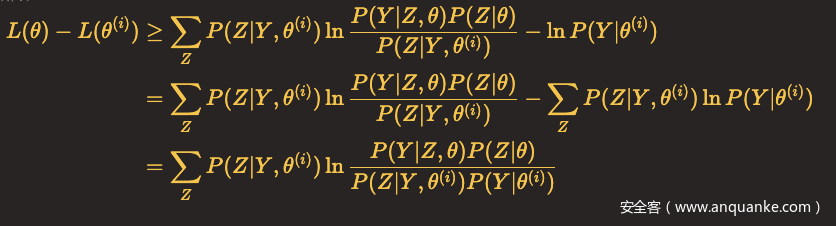
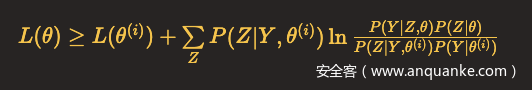
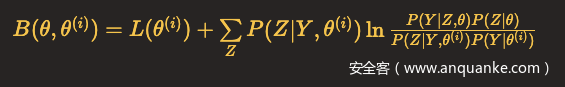
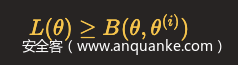


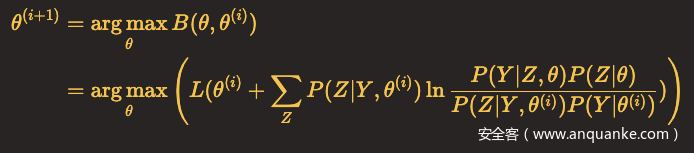
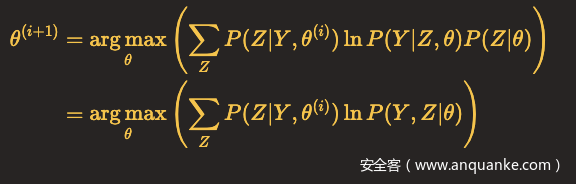

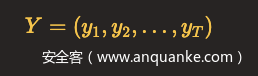



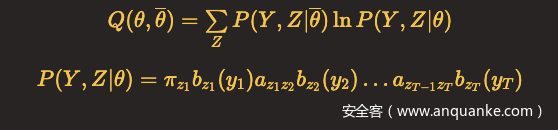
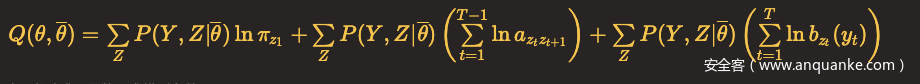
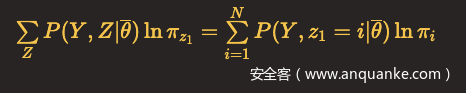




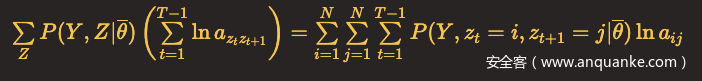
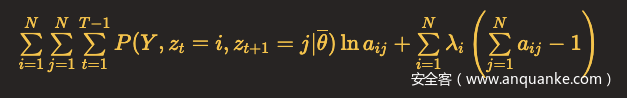
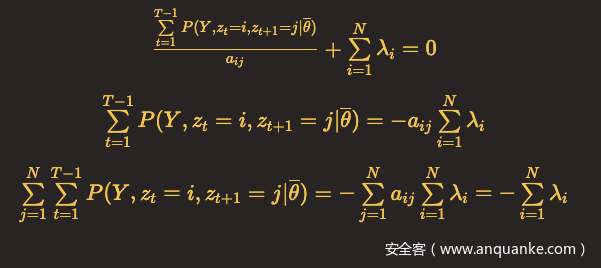
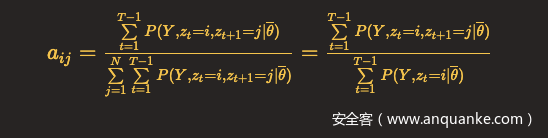
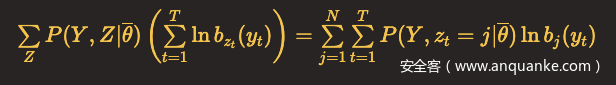
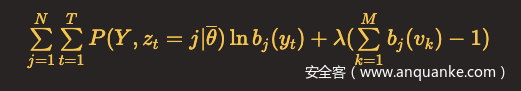
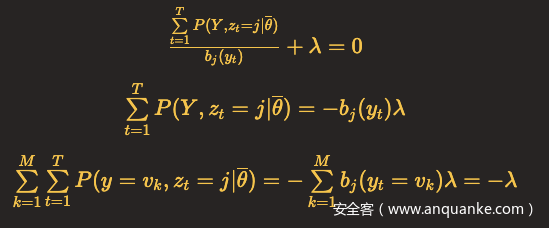
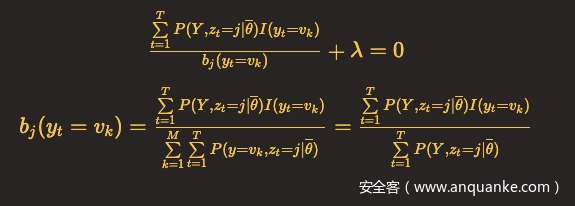







发表评论
您还未登录,请先登录。
登录