2021 蓝帽杯 Final RE Writeup

 

abc

题目中存在着大量的花指令来妨碍我们查看伪代码，我们这里尝试编写 IDAPython 脚本来去除花指令。

花指令分析

TYPE1

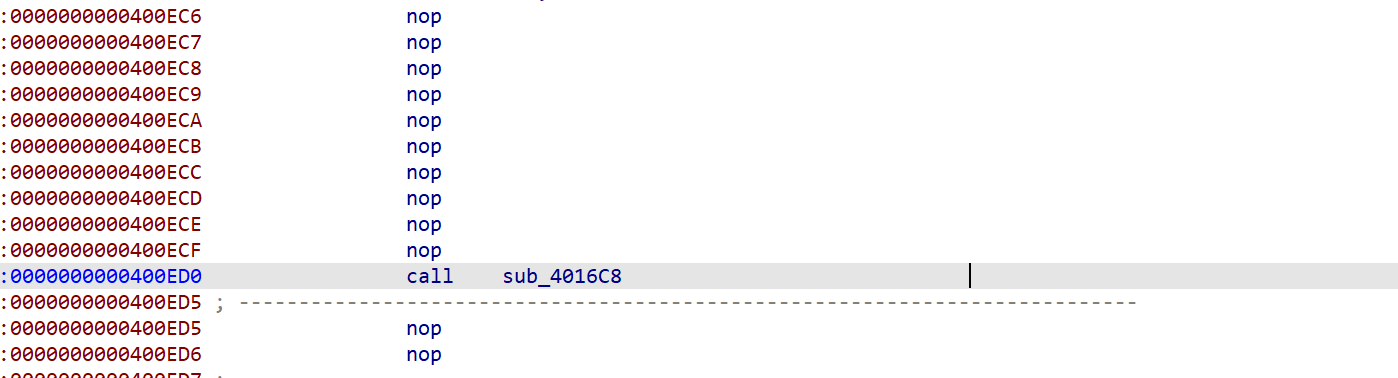
call $+5

其实相当于往栈上写一个返回地址（0x400ECB），并且由于 CALL 指令的长度就是 5，所以实际上程序在执行 CALL 之后的 RIP （0x400ECB）不变。

add qword ptr [rsp], 0Ch

相当于把前面压如的 RIP 地址 + 0xC，计算可以得知（0x400ECB + 0xC = 0x400ED7），也就是说实际上后面解析出来的 leave 和 retn 并不会执行，只是起到了混淆反编译器的作用。

jmp sub_4016C8

这里跳转的实际上是一个 plt 函数位置，但是这里使用了 jmp sub_4016C8 这种方法调用，在函数内部 retn 的时候就会直接返回到 0x400ED7 这个位置。

根据以上分析可知，实际上程序所做的就是将 call sub_4016C8 混淆为以上指令来阻碍 IDA Pro 的分析，而我们所需要做的，就是把上述代码还原为 call sub_4016C8。

还原效果

TYPE2

插入两部分的无效片段

插入了一个函数

push    rbp
mov     rbp, rsp
leave
retn

程序会调用这个函数，但是实际上没有任何意义（为了混淆 IDA 识别）

执行后会使用 jmp 直接跳出，jmp 后的 leave 和 retn 不会被执行。

其特征为垃圾代码存在于 call 函数和 jmp 指令之间，只需要 nop 掉这一部分的内容即可。

还原效果

TYPE3

这个实际上就是 leave;retn，我们直接还原即可

还原效果

修复 PLT 符号信息

解决以上三种花指令后，查看伪代码就稍微好看一些了，但是 PLT 符号仍然没有被加载显示

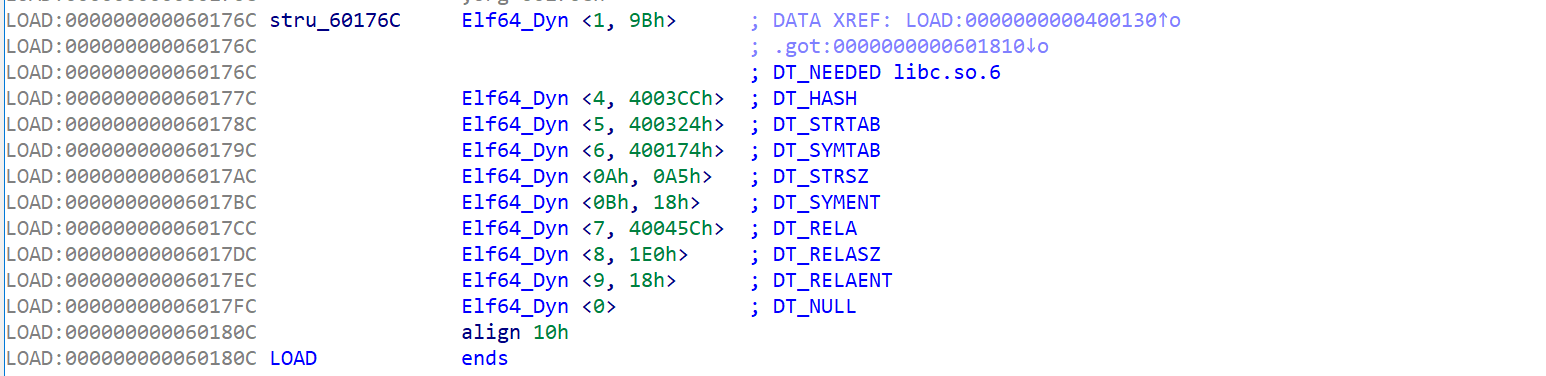
开头的那三个调用明显是 setbuf，但是没有被显示，我怀疑是因为 Dyn 这里没有 DT_JMPREL，导致 IDA 没有识别

但是实际上在 DT_RELA 中存在 R_X86_64_JUMP_SLOT 信息，也就是我们可以根据这里的信息来模拟 PltResolver 从而恢复 Plt 的符号数据 。

这部分的思路来自于 https://github.com/veritas501/PltResolver

还原常量数据

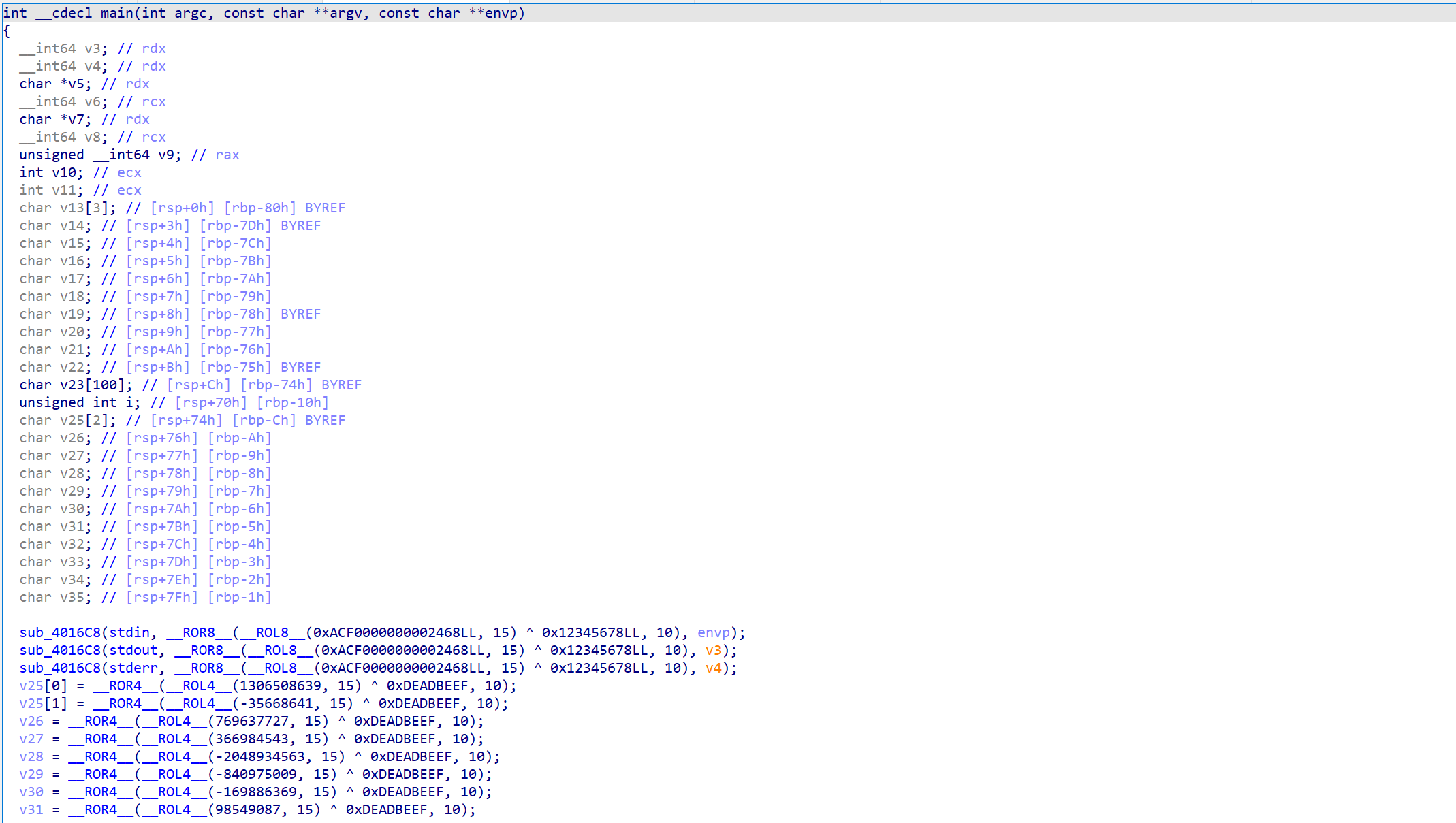
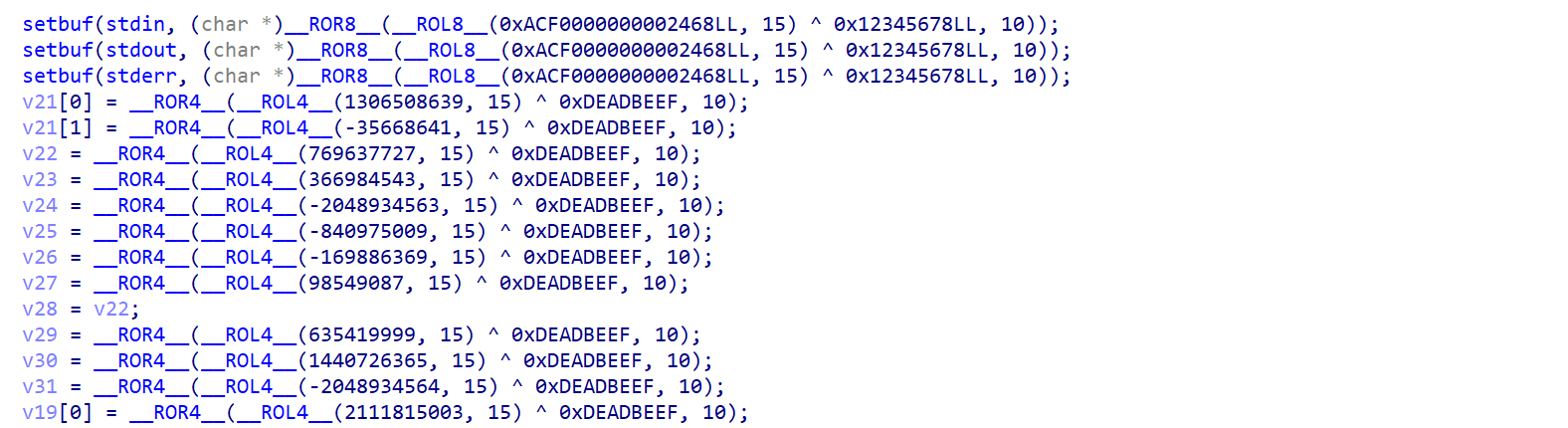
仔细观察就可以发现在程序中存在着大量的常量混淆，使用 ROR8 ROL8 ROR4 ROL4 这样的移位指令来妨碍分析

查看汇编代码发现格式基本上如下所示

我们可以直接计算这些操作，最终优化为直接的 mov rax, xxx

具体的实现逻辑就是，搜索 mov rax, xxx 这样的指令，然后以此指令向下遍历，遍历到 xor，rol，ror 这样可以直接优化的指令则模拟计算，计算完成后再修改 mov rax 指令。在计算的过程中需要考虑到操作数是 32 位还是 64 位，对于不同的操作手法。

还原效果

程序虽然还有一层取反操作后才输出，但是这对于我们分析程序逻辑已经影响不大了，所以我们接下来就可以直接进行分析。

主程序分析

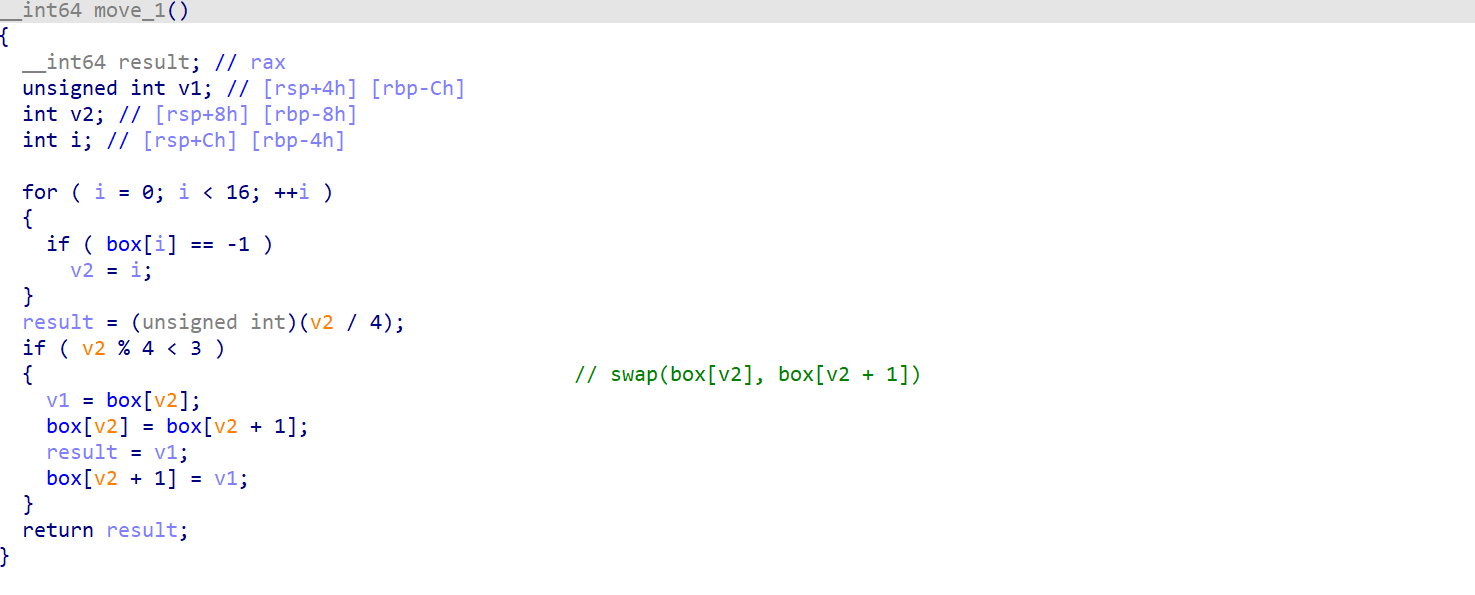
程序要求输入一串操作序列，输入的序列可以操作内部的 box 进行移动

这个移动的过程就是在不溢出过边界的情况下，可以让 box 中的 -1 向上下左右任意一个方向移动（交换相邻块）

简单的研究后，可以发现这个游戏其实就是 15 puzzle-game

也就是要求操作类似上面的空白块（可以上下左右移动），最后让空白块的位置停留在右下角且其他内容依次增加

这一部分就是 check 的代码，如果你的操作序列完成了游戏，那么就会使用 system 来 cat flag，这样做的原因是，这种游戏的路径通常是有多条的，使用远程服务器验证序列的方式来 cat flag，可以让多解都能够得到 Flag，这也是一种常用的解决方案。

这里我通过搜索在 github 上找到一个脚本可以跑出结果

#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <stack>
#include <queue>
#include <cstdlib>

using namespace std;

const string SOLUTION = "010203040506070809101112131415SS";

struct Node {
    string state;
    string path;
};

bool goalTest(Node a) {
    return (a.state.compare(SOLUTION) == 0);
}

string swapNew(string state, unsigned int a, unsigned int b) {
    string newState(state);
    string temp = newState.substr(a, 2);
    newState[a] = newState[b];
    newState[a + 1] = newState[b + 1];
    newState[b] = temp[0];
    newState[b + 1] = temp[1];
    return newState;
}

void generateSuccessors(Node curNode, vector<Node>& possible_paths) {
    int loc = curNode.state.find("SS");
    // cout << "SS: " << loc << endl;
    if (loc > 7) { //can move up?e
        Node newNode;
        newNode.state = swapNew(curNode.state, loc, loc - 8);
        newNode.path = curNode.path;
        newNode.path += 'u';
        possible_paths.push_back(newNode);
    }
    if (loc < 24) { //can move down?
        Node newNode;
        newNode.state = swapNew(curNode.state, loc, loc + 8);
        newNode.path = curNode.path;
        newNode.path += 'd';
        possible_paths.push_back(newNode);
    }
    if (loc % 8 < 6) { //can move right?
        Node newNode;
        newNode.state = swapNew(curNode.state, loc, loc + 2);
        newNode.path = curNode.path;
        newNode.path += 'r';
        possible_paths.push_back(newNode);
    }
    if (loc % 8 > 1) { //can move left?
        Node newNode;
        newNode.state = swapNew(curNode.state, loc, loc - 2);
        newNode.path = curNode.path;
        newNode.path += 'l';
        possible_paths.push_back(newNode);
    }
}

Node bfs(Node startNode) {
    queue<Node> frontier; //list for next nodes to expand
    frontier.push(startNode);
    map<string, int> expanded; //keeps track of nodes visited
    int numExpanded = 0;
    int maxFrontier = 0;
    while (!frontier.empty()) {
        Node curNode = frontier.front();
        frontier.pop();
        numExpanded += 1;
        expanded[curNode.state] = 1;
        vector<Node> nextNodes;
        generateSuccessors(curNode, nextNodes);
        for (unsigned int i = 0; i < nextNodes.size(); i++) {
            if (goalTest(nextNodes[i])) {
                cout << "Expanded: " << numExpanded << " nodes" << endl;
                cout << "Max Frontier: " << maxFrontier << " nodes" << endl;
                cout << nextNodes[i].state << endl;
                return nextNodes[i];
            }
            if (expanded.find(nextNodes[i].state) != expanded.end()) {
                continue;
            }
            frontier.push(nextNodes[i]);
            if (frontier.size() > maxFrontier) {
                maxFrontier = frontier.size();
            }
        }
    }
}

Node dfs(Node startNode, int maxDepth = 80) {
    stack<Node> frontier;
    frontier.push(startNode);
    map<string, int> expanded;
    int numExpanded = 0;
    int maxFrontier = 0;
    while (!frontier.empty()) {
        Node curNode = frontier.top();
        frontier.pop();
        expanded[curNode.state] = curNode.path.length();
        numExpanded += 1;
        vector<Node> nextNodes;
        //cout << curNode.path << endl;
        generateSuccessors(curNode, nextNodes);
        for (unsigned int i = 0; i < nextNodes.size(); i++) {
            if (nextNodes[i].path.length() > maxDepth) {
                continue;
            }
            if (goalTest(nextNodes[i])) {
                cout << "Expanded: " << numExpanded << " nodes" << endl;
                cout << "Max Frontier: " << maxFrontier << " nodes" << endl;
                return nextNodes[i];
            }
            if (expanded.find(nextNodes[i].state) != expanded.end()
                && expanded[nextNodes[i].state] < nextNodes[i].path.length()) {
                continue;
            }
            frontier.push(nextNodes[i]);
            if (frontier.size() > maxFrontier) {
                maxFrontier = frontier.size();
            }
        }
    }
    return startNode;
}

Node ittdfs(Node startNode) {
    for (unsigned int i = 1; i < 80; i++) {
        //cout << "current iteration: " << i << endl;
        Node solved = dfs(startNode, i);
        if (goalTest(solved)) {
            //cout << "max depth: " << i << endl;
            return solved;
        }
    }
    return startNode;
}

int main(int argc, char* argv[]) {
    Node startNode;
    startNode.state = "";
    int method = 4;
    startNode.state = "011002030513060409SS071114151208";
    if (startNode.state.length() != 32) {
        cout << "Please enter the state of the puzzle using 2 digits for each position"
            << " and SS for the empty space" << endl;
        cout << "Example Usage: " << argv[0] << "010203040506070809101112131415SS" << endl;
        return 1;
    }
    // vector<Node> test;
    // generateSuccessors(startNode,test);
    // for (int i = 0; i < test.size(); i++){
    //     cout << test[i].state << " " << test[i].path << endl;
    int depth;
    Node solved;
    switch (method) {
    case 1: //bfs
        cout << "BFS USED" << endl;
        solved = bfs(startNode);
        break;
    case 2: //dfs
        cout << "DFS USED" << endl;
        solved = dfs(startNode);
        break;
    case 3: //limited dfs
        cout << "depth limited DFS USED" << endl;
        if (argc < 4) {
            cout << "Need a third parameter for maximum depth" << endl;
            return 1;
        }
        depth = atoi(argv[3]);
        solved = dfs(startNode, depth);
        break;
    case 4:
        cout << "ITTERATIVE DFS USED" << endl;
        solved = ittdfs(startNode);
        break;
    }

    if (!goalTest(solved)) {
        cout << "No solution found" << endl;
        return 1;
    }

    cout << "path to solution: " << solved.path << endl;
    return 0;
}

等待程序跑完后，我们替换操作指令为程序所设定的，最终得到操作序列

$$%@@#$#@#@%%%$$$###@@@

提交操作序列到远程的服务器，最终即可得到 FLAG 数据。

IDAPython 脚本

其实这道题的花指令量不算大，所以手动处理也是可以的，但是相对于手动处理，使用脚本进行批量处理的进阶要更高，所以在赛后我尝试使用 IDAPython 来处理这个程序中的花指令，并借此机会学习 IDAPython。在此分享一下我的脚本，虽然不是最优的写法，但是在此题中也算够用。

import ida_ida
import idaapi
import idautils
import idc


def patch_raw(address, patch_data, size):
    ea = address
    orig_data = ''
    while ea < (address + size):
        if not idc.has_value(idc.get_full_flags(ea)):
            print("FAILED to read data at 0x{0:X}".format(ea))
            break
        orig_byte = idc.get_wide_byte(ea)
        orig_data += chr(orig_byte)
        patch_byte = patch_data[ea - address]
        if patch_byte != orig_byte:
            # patch one byte
            if idaapi.patch_byte(ea, patch_byte) != 1:
                print("FAILED to patch byte at 0x{0:X} [0x{1:X}]".format(ea, patch_byte))
                break
        ea += 1
    return (ea - address, orig_data)


def nop(addr, endaddr):
    while (addr < endaddr):
        idc.patch_byte(addr, 0x90)
        addr += 1


def undefine(addr, endaddr):
    while addr < endaddr:
        idc.del_items(addr, 0)
        addr += 1


def GetDyn():
    phoff = idc.get_qword(ida_ida.inf_get_min_ea() + 0x20) + ida_ida.inf_get_min_ea()
    phnum = idc.get_wide_word(ida_ida.inf_get_min_ea() + 0x38)
    phentsize = idc.get_wide_word(ida_ida.inf_get_min_ea() + 0x36)
    for i in range(phnum):
        p_type = idc.get_wide_dword(phoff + phentsize * i)
        if p_type == 2:  # PY_DYNAMIC
            dyn_addr = idc.get_qword(phoff + phentsize * i + 0x10)
            return dyn_addr


def ParseDyn(dyn, tag):
    idx = 0
    while True:
        v1, v2 = idc.get_qword(dyn + idx * 0x10), idc.get_qword(dyn + idx * 0x10 + 8)
        if v1 == 0 and v2 == 0:
            return
        if v1 == tag:
            return v2
        idx += 1


def SetFuncFlags(ea):
    func_flags = idc.get_func_attr(ea, idc.FUNCATTR_FLAGS)
    func_flags |= 0x84  # FUNC_THUNK|FUNC_LIB
    idc.set_func_attr(ea, idc.FUNCATTR_FLAGS, func_flags)


def PltResolver(rela, strtab, symtab):
    idx = 0
    while True:
        r_off = idc.get_qword(rela + 0x18 * idx)
        r_info1 = idc.get_wide_dword(rela + 0x18 * idx + 0x8)
        r_info2 = idc.get_wide_dword(rela + 0x18 * idx + 0xc)
        r_addend = idc.get_qword(rela + 0x18 * idx + 0x10)
        if r_off > 0x7fffffff:
            return
        if r_info1 == 7:
            st_name = idc.get_wide_dword(symtab + r_info2 * 0x18)
            name = idc.get_strlit_contents(strtab + st_name)
            # rename got
            idc.set_name(r_off, name.decode("ascii") + '_ptr')
            plt_func = idc.get_qword(r_off)
            # rename plt
            idc.set_name(plt_func, 'j_' + name.decode("ascii"))
            SetFuncFlags(plt_func)
            # rename plt.sec
            for addr in idautils.DataRefsTo(r_off):
                plt_sec_func = idaapi.get_func(addr)
                if plt_sec_func:
                    plt_sec_func_addr = plt_sec_func.start_ea
                    idc.set_name(plt_sec_func_addr, '_' + name.decode("ascii"))
                    SetFuncFlags(plt_sec_func_addr)
                else:
                    print("[!] idaapi.get_func({}) failed".format(hex(addr)))
        idx += 1


def rol(n, k, word_size=None):
    k = k % word_size
    n = (n << k) | (n >> (word_size - k))
    n &= (1 << word_size) - 1
    return n


def ror(n, k, word_size=None):
    return rol(n, -k, word_size)


def dejunkcode(addr, endaddr):
    while addr < endaddr:
        idc.create_insn(addr)
        # TYPE 1
        if idc.print_insn_mnem(addr) == 'call' and idc.get_operand_value(addr, 0) == addr + 5:
            if idc.print_insn_mnem(addr + 5) == 'add' and idc.get_operand_value(addr + 5, 0) == 4:  # rsp
                add_size = idc.get_operand_value(addr + 5, 1)
                if idc.print_insn_mnem(addr + 0xa) == 'jmp':
                    idc.patch_byte(addr + 0xa, 0xE8)
                    call_addr = idc.get_operand_value(addr + 0xa, 0)
                    nop(addr, addr + 0xa)
                    next_op = addr + 0x5 + add_size
                    nop(addr + 0xa + 0x5, next_op)
                    addr = next_op
                    continue
        # TYPE 2
        if idc.print_insn_mnem(addr) == 'call' and idc.print_insn_mnem(addr + 5) == 'jmp':
            call_addr = idc.get_operand_value(addr, 0)
            if idc.get_bytes(call_addr, 6) == b'\x55\x48\x89\xE5\xC9\xC3':
                '''
                push    rbp
                mov     rbp, rsp
                leave
                retn
                '''
                nop(addr, addr + 5)  # nop call
                nop(addr + 0xa, call_addr + 6)
                undefine(call_addr, call_addr + 6)
        # TYPE 3
        if idc.print_insn_mnem(addr) == 'leave':
            if idc.print_insn_mnem(addr + 1) == 'add' and \
                    idc.get_operand_value(addr + 1,0) == 4 and idc.get_operand_value(addr + 1, 1) == 8: #add rsp, 8

                if idc.print_insn_mnem(addr + 1 + 4) == 'jmp' and idc.get_operand_value(addr + 1 + 4,
                                                                                        0) == 0xfffffffffffffff8:  # [rsp - 8]
                    nop(addr + 1, addr + 1 + 4 + 4)
                    idc.patch_byte(addr + 1 + 4 + 3, 0xC3)

        # TYPE 4
        REGS = [0, 1] #[RAX, RCX]
        if idc.print_insn_mnem(addr) == 'mov' and \
                (idc.get_operand_type(addr, 0) == idc.o_reg and idc.get_operand_value(addr, 0) in REGS)\
                and idc.get_operand_type(addr, 1) == idc.o_imm:  # rax

            if idc.get_item_size(addr) > 5:
                op2_size = 8
            else:
                op2_size = 4

            op2 = idc.get_operand_value(addr, 1)
            next_op = addr
            print('begin:\t' + hex(addr))
            while next_op < endaddr:
                next_op += idc.get_item_size(next_op)
                if idc.get_operand_type(next_op, 0) == idc.o_reg and idc.get_operand_value(next_op, 0) in REGS\
                        and idc.get_operand_type(next_op, 1) == idc.o_imm:  # mov rax|rcx, xxx
                    next_op_insn = idc.print_insn_mnem(next_op)
                    da = idc.get_operand_value(next_op, 1)

                    log_data = next_op_insn + " " + hex(op2) + ", " + hex(da) + " -> "

                    if next_op_insn == "rol":
                        op2 = rol(op2, da, 8 * op2_size)
                    elif next_op_insn == "ror":
                        op2 = ror(op2, da, 8 * op2_size)
                    elif next_op_insn == "xor":
                        op2 = op2 ^ da
                        if op2_size == 8:
                            op2 &= 0xffffffffffffffff
                        else:
                            op2 &= 0xffffffff
                    else:
                        break
                    log_data += hex(op2)
                    print(log_data)
                else:
                    break
            print("end:\t", hex(next_op))
            if op2_size == 8:
                patch_raw(addr + 2, op2.to_bytes(length=op2_size, byteorder='little'), op2_size) #mov rax, xxx
                nop(addr + 0xA, next_op)
            else:
                patch_raw(addr + 1, op2.to_bytes(length=op2_size, byteorder='little'), op2_size)  # mov rax, xxx
                nop(addr + 5, next_op)
            addr = next_op
            continue

        addr += idc.get_item_size(addr)


dejunkcode(0x0000000000400672, 0x000000000040151B)

dyn = GetDyn()
print("Elf64_Dyn:\t" + hex(dyn))
strtab = ParseDyn(dyn, 0x5)
symtab = ParseDyn(dyn, 0x6)
rela = ParseDyn(dyn, 0x7)
print("DT_STRTAB:\t" + hex(strtab))
print("DT_SYMTAB:\t" + hex(symtab))
print("DT_RELA:\t" + hex(rela))
PltResolver(rela, strtab, symtab)

 

executable_pyc

上面的题目，我觉得难度都蛮大的，不过都很不幸被打成了签到题，这可能就是线上比赛所必须要面对的吧。而这道题目直到比赛结束也只有 2 解，在比赛中我也没有做出，赛后复现后在这里进行分享，感谢密码爷的帮助~

还原字节码至源码

这道题目所给的是一个 pyc 文件，但是对文件进行了混淆，使得直接使用工具进行转化为源码报错，混淆总共有两处，我们尝试更改源码即可反编译得到字节码内容。

我们这里使用调试的方法来得到混淆的位置并尝试还原

import sys
import decompyle3
decompyle3.decompile_file(r"C:\en.pyc", outstream=sys.stdout)

直接执行以上程序发现程序卡在

在 pyc 文件中搜索（0x4f），并且修改为 0（使其不溢出）

修改之后我们就可以查看字节码信息了，到这里其实就可以尝试手动恢复了，但是我继续尝试直接恢复出源码的信息。

可以看到字节码的开头是这样的两行

 L.   1         0  JUMP_FORWARD          4  'to 4'
                2  LOAD_CONST               0
              4_0  COME_FROM             0  '0'
                4  LOAD_CONST               0
                6  LOAD_CONST               None

我们可以知道实际上执行的时候会直接跳过第二行的内容（存在溢出的 0x4f），但是对于反编译器来说，会对字节码进行逐行解析，因此导致了反编译认为此处存在非法指令。

我们这里直接把开头的这四个字节的内容替换为 09（NOP）指令

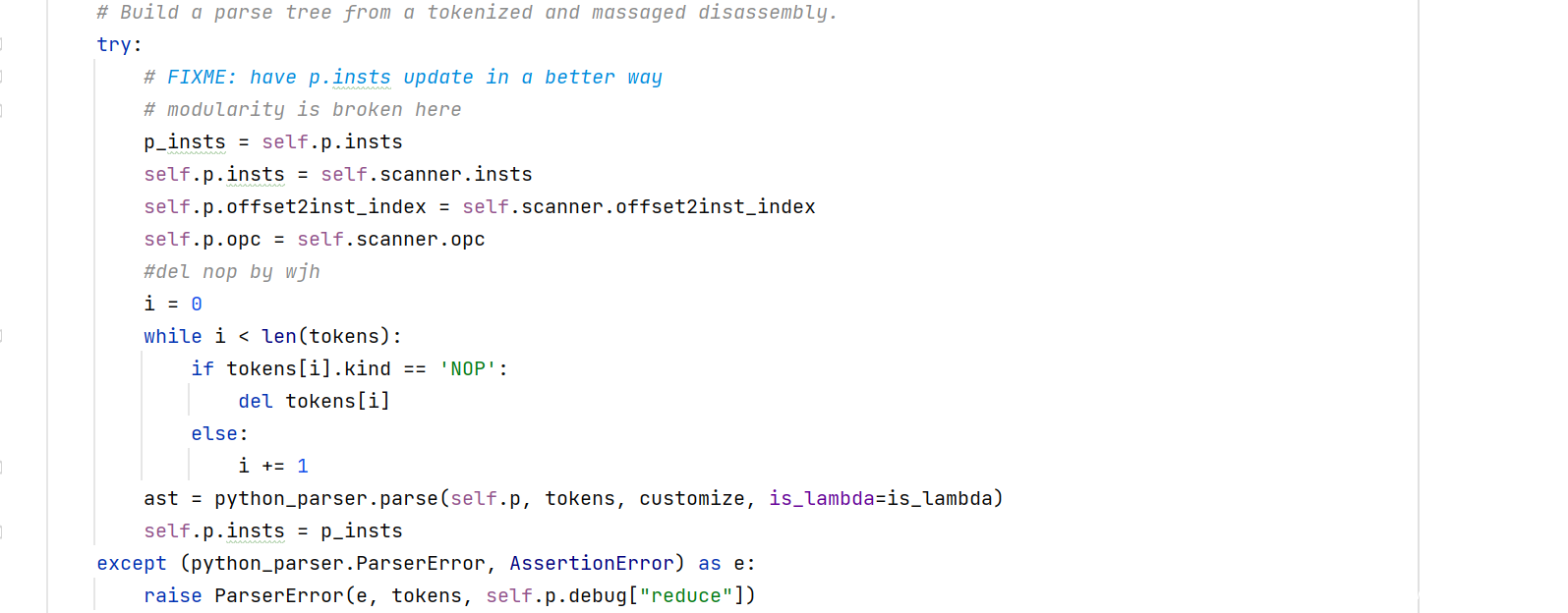
并且在 decompyle3/semantics/pysource.py 中这个位置增加以下代码来删除 NOP 指令（可以根据搜索关键字来找到）

i = 0
while i < len(tokens):
    if tokens[i].kind == 'NOP':
        del tokens[i]
    else:
        i += 1

修改后，程序就会在另一处报错

Instruction context:

 L.  38        16  LOAD_GLOBAL          63  63
                  18  LOAD_FAST            77  '77'
->                20  CALL_FUNCTION_31     31  '31 positional arguments'
                  22  LOAD_CONST               512
                  24  COMPARE_OP               <
                  26  POP_JUMP_IF_TRUE     47  'to 47'
                  28  LOAD_GLOBAL              AssertionError
                  30  RAISE_VARARGS_1       1  'exception instance'
                32_0  COME_FROM            10  '10'

意思应该就是这里 CALL_FUNCTION_31 存在错误（31 的意思是有 31 个参数要传入函数），这个明显是过多的，这里我经过尝试，发现修改为 1 即可不报错，具体的原因我不得而知，希望有知道的师傅可以在评论区指点一番！

再次执行即可得到源码数据

import gmpy2 as g
from Crypto.Util.number import long_to_bytes, bytes_to_long
import random

def gen_num(n_bits):
    res = 0
    for i in range(n_bits):
        if res != 0:
            res <<= 1
        else:
            res |= random.choice([0, 1])

    return res


def gen_prime(n_bits):
    res = gen_num(n_bits)
    while not g.is_prime(res):
        b = 1
        while b != 0:
            res, b = res ^ b, (res & b) << 1

    return res


def po(a, b, n):
    res = 1
    aa = a
    while b != 0:
        if b & 1 == 1:
            res = res * aa % n
        else:
            aa *= aa
            b >>= 1

    return res % n


def e2(m):
    assert type(m) == bytes
    l = len(m) // 2
    m1 = bytes_to_long(m[:l])
    m2 = bytes_to_long(m[l:])
    p = gen_prime(1024)
    q = gen_prime(1024)
    pp = g.next_prime(p + 2333)
    qq = g.next_prime(q + 2333)
    e = g.next_prime(65535)
    ee = g.next_prime(e)
    n = p * q
    nn = pp * qq
    c1 = long_to_bytes(pow(m1, e, n))
    c2 = long_to_bytes(pow(m2, ee, nn))
    print(str(n), nn.digits(), (c1 + c2).hex())
    return c1 + c2


if __name__ == '__main__':
    import sys
    if len(sys.argv) >= 2:
        e2(sys.argv[1].encode())
    else:
        import base64 as B
        flag = B.b64decode(b'ZmxhZ3t0aGlzaXNhZmFrZWZsYWdhZ2Fhc2FzaGRhc2hkc2hkaH0=')
        e2(flag)

解密 Flag

这一部分的操作实际上完全就是一道 Crypto 的题目，我在比赛过程中就是卡在了这里，赛后我问了群里的密码师傅（感谢！！），最终问题得到了解决，这里简单的说一下解法和我的理解。

next_prime 这个函数寻找的质数与传入的参数基本上差值都在 1500 以内，所以 pp 和 qq 这两个质数实际上是非常接近 p 和 q 这两个质数的，而且在可爆破的范围内，设为 d1 和 d2。

所以可以得到

计算得到 p 和 q，pp 和 qq，由于 flag 内容是两部分 bytes 拼接，所以可以爆破分隔位置求解。

计算程序

import gmpy2
from Crypto.Util.number import long_to_bytes, bytes_to_long
n = 10300808326934539089496666241808264289631957459372648156286399524715435483257526083909012656240599916663153630994400397551123967736269088895097145175999170121832669199408651009372742448196961434772052680714475103278704994244915332148949308972258132346198706995878511207707020032852291909422169657384059305615332901933166314692127020030962059133945677194815714731744932280037687773557589292839426111679593131496468880818820566335362063945141576571029271455695757725169819071536590541808603312689890186432713168331831945391117398124164372551511615664022982639779869597584768094658974144703654232643726744397158318139843
nn = 10300808326934539089496666241808264289631957459372648156286399524715435483257526083909012656240599916663153630994400397551123967736269088895097145175999170121832669199408651009372742448196961434772052680714475103278704994244915332148949308972258132346198706995878511207707020032852291909422169657384059306119730985949350246133999803589372738154347587848281413687500584822677442973180875153089761224816081452749380588888095064009160267372694200256546854314017937003988172151851703041691419537865664897608475932582537945754540823276273979713144072687287826518630644255675609067675836382036436064703619178779628644141463
c = "22cca5150ca0bb2132f68302dc7441e52b91ae7252e44cc13ed83e58253a9aaaa55e095ba36748dff7ea21fff553f8c4656e77a508b64da054f1381b7e2d0600bcec6ed9e1cc8d14c2362aaef7a972a714f88e5afb2d39e2d77d0c22a449ca2cfb0802c138f20e0ecbd3c174151cdb8e8ca6d89aa3c503615ebfbc851af5ac51dcfa8b5869b775b57a27b9e4346979180d89b303cae2c5d9e6cabb3c9947837bd8f92333532d4b54dd72ea354000600066328f6f4329147df195ec78a7ab9d39973ce0fd6511e7a0de54737bee64476ba531604f0375b08adf7d768c41ba9e2ba88468d126561a134de79dc0217c1c56d219ca6747103618e46f35281feb9e6050c93e32e26e21ee2c3d495f60db2fad9f9a5c570c9f97aee698024ebff6163ef26e32958872db7c593d7f41f90981b8db45aa01085be1e61f7603ecf3d5c032dd90dea791cd9825299548c0cbe7dadabc157048a7fd5cd4bcb1cfeaf0bd2d679f66ceb0b1c33ec04bd20317f872c85d500a3475833f983fdee59b3f61a731e2a8b9a60bd7d840f46e97f06dd4fd8ad1cb4d13a82da01938801c33835ceaf34e1cf62ebdde7ac68b17c2a236b64ffacd2a0e7258571ce570871aea9ff309df63c0a3abcfa0c05d159a82f9fa3f3ad73944e4ae33c3432c8b65c0d6fe9b560220b14abe5886188fc1e6afa4bb4395669618387224422acf20b519af902225e270"
d = nn - n
q = 0
for d1 in range(2333, 3000):
    for d2 in range(2333, 3000):
        t = d - d1 * d2
        k = t * t - 4 * d1 * d2 * n
        if k > 0 and gmpy2.iroot(k, 2)[1]:
            q = (t + gmpy2.iroot(k, 2)[0]) // (2 * d1)
            p = n // q
            e = 65537
            ee = gmpy2.next_prime(e)
            d1 = gmpy2.invert(e, (p - 1) * (q - 1))
            pp = gmpy2.next_prime(p + 2333)
            qq = gmpy2.next_prime(q + 2333)
            d2 = gmpy2.invert(ee, (pp - 1) * (qq - 1))
            for l in range(1, len(c)):
                c1, c2 = int(c[:l], 16), int(c[l:], 16)
                if c1 < n and c2 < nn:
                    flag = long_to_bytes(pow(c1, d1, n)) + long_to_bytes(pow(c2, d2, nn))
                    if "flag" in flag:
                        print(flag)

 

总结

这次的蓝帽杯的RE题目难度还是比较高的，我认为还是有很多值得学习点，并且从这些题目中可以看出，RE的题目以及逐渐往自动化和 Crypto 方向靠拢，在题目中经常会结合一些其他方向的知识，如果想要在比赛中快速的解题，掌握一些其他方向的知识也是必不可少的。本文中的方法不一定是最好最快的，但是一定是能够让做题者在做题的过程中学习到一些知识的，希望在比赛过程中即使做出题目的师傅，也可以尝试着跟着本篇文章的思路来解题。本文在编写的过程中有些仓促，难免有些地方存在错误和没有阐述清楚，希望有疑问或者看到错误的师傅可以在评论区与我交流。