比赛时遇到这道题目,花了两个多小时才做出来。赛后又仔细看了看题,觉得比较有意思,因此来分享一下我的解题过程,方便大家复现赛题。
题目分为 check1 和 check2 两个部分,要求完成两个部分的解密即可得到 flag,其中两个部分内还分为几个小问题,我这里全部使用 Z3 来解决。
第一部分
约束一
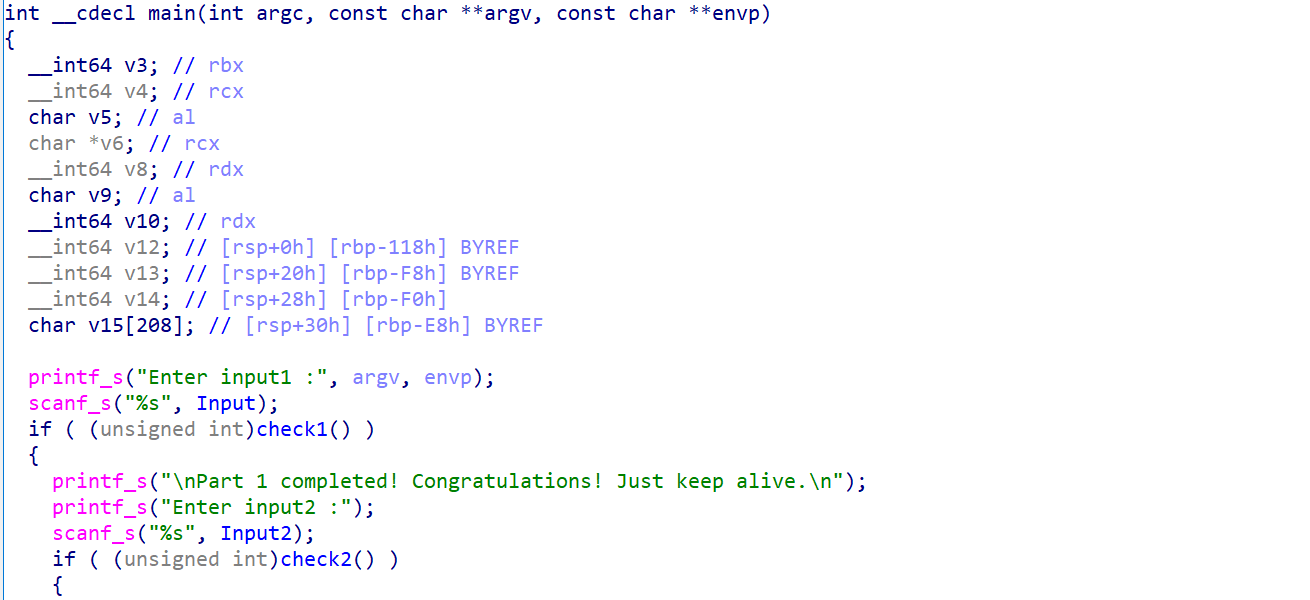
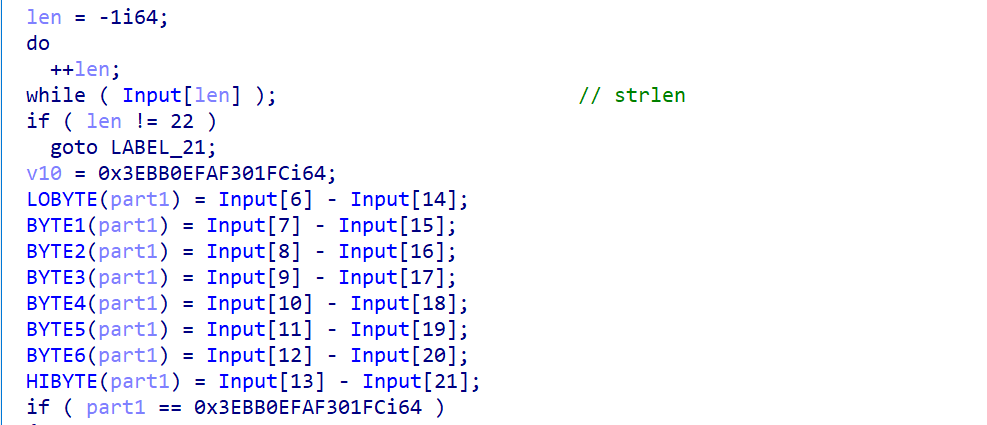
这部分提供了一个约束条件,首先是要求第一部分输入的长度为 22,并且给出了以下约束
Input[6] - Input[14] = 0xFC
Input[7] - Input[15] = 0x01
Input[8] - Input[16] = 0xF3
Input[9] - Input[17] = 0xFA
Input[10] - Input[18] = 0x0E
Input[11] - Input[19] = 0xBB
Input[12] - Input[20] = 0x3E
Input[13] - Input[21] = 0x00
约束二
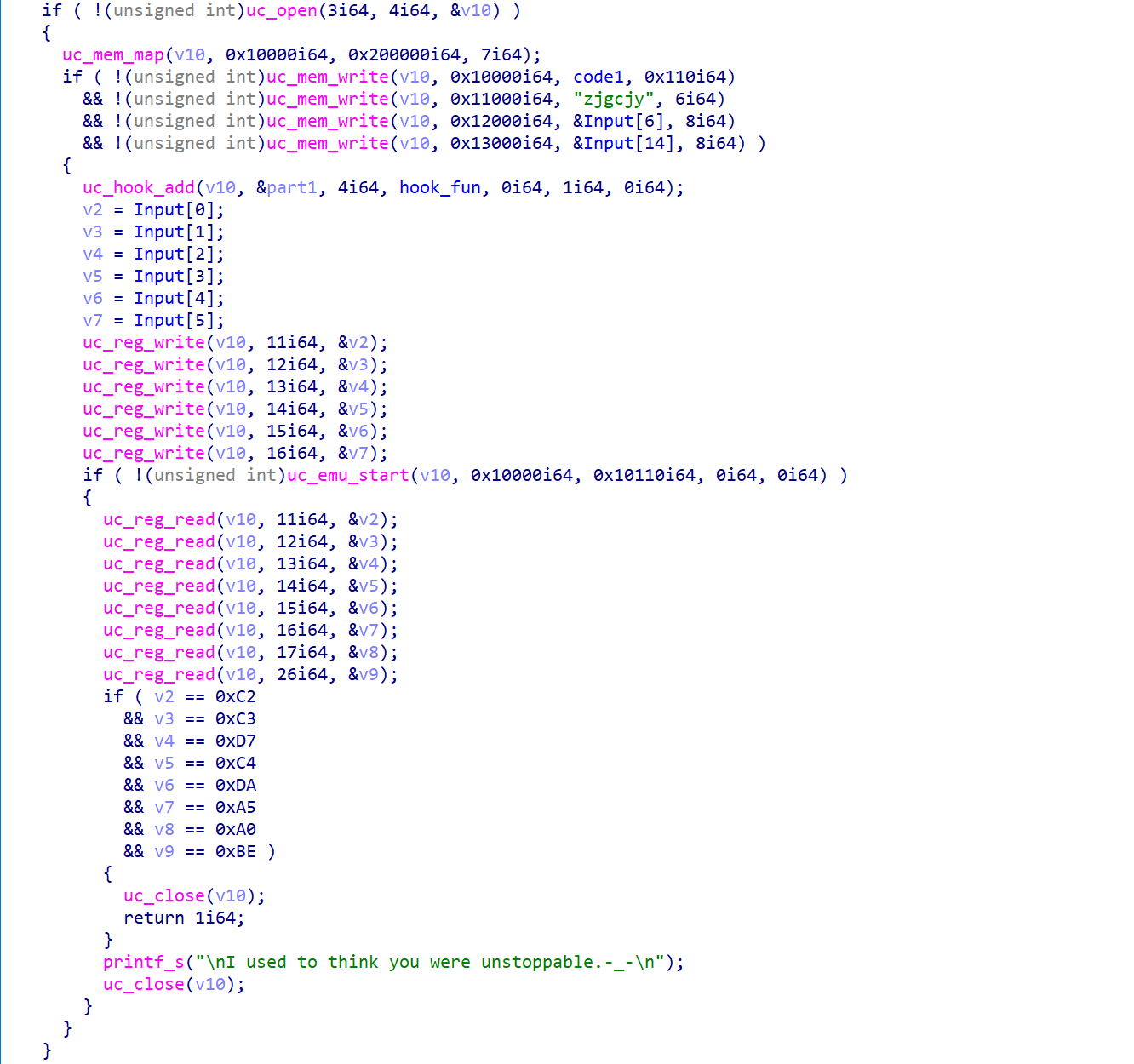
这部分内容就来自于 unicorn 的模拟执行
这部分内容的逻辑比较清楚,但是其中一些常数我们无法得知含义,而且此比赛要求离线,所以我考虑从我本地安装的 python 版 unicorn 库中找到这些常数。
我之前正好写过一题 unicorn 的题(感谢 TCTF),找到启动内容大致如下,猜测这个启动和 C 实现中的 uc_open 类似,所以常数应该也是对应的。
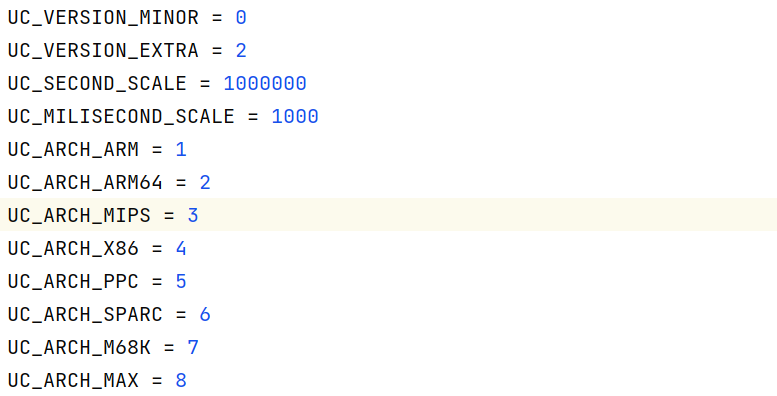
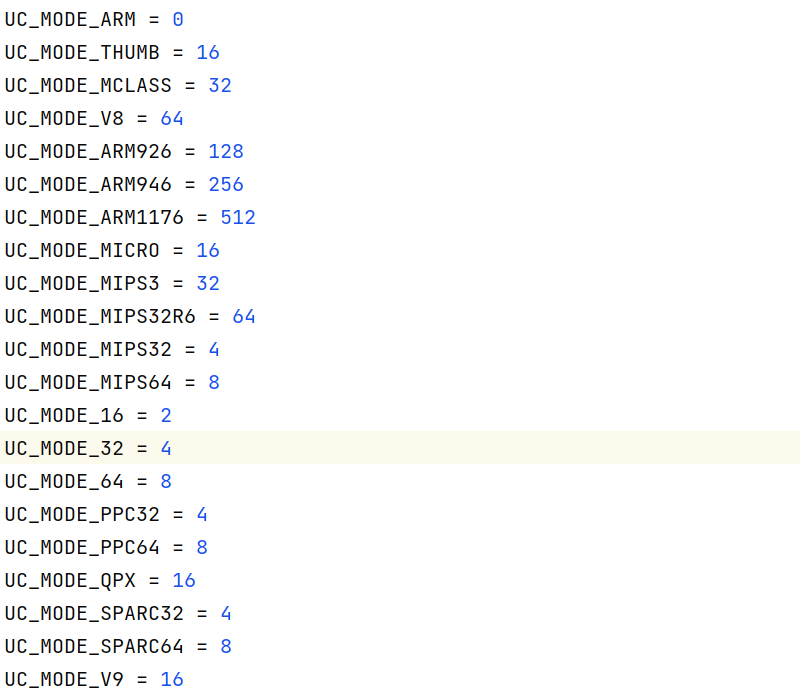
在代码中分别传入的常数是 3 和 4,我们在常数定义中分别找到这两个内容。
3 代表的就是 MIPS 架构
4 代表的是 32 位
所以我们知道接下来要模拟的代码就是 32 位的 MIPS 代码,这便于我们后续分析。
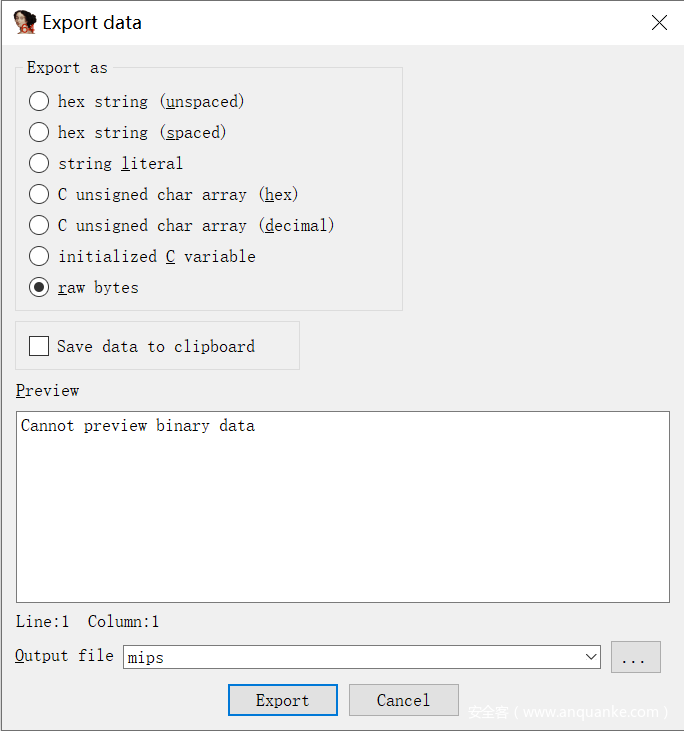
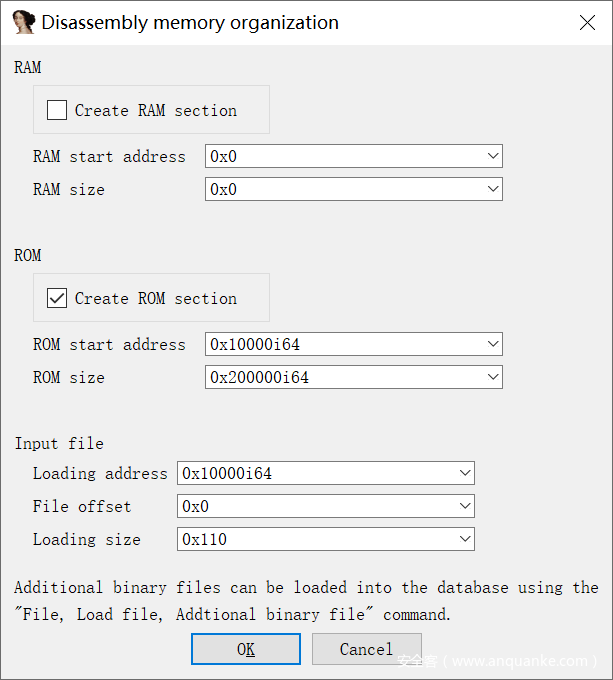
后续可以看到在 0x10000 处写入了 MIPS 汇编代码,根据写入长度,定义字节长度为 0x110,再用 IDA 的 Ctrl + E 将其提取
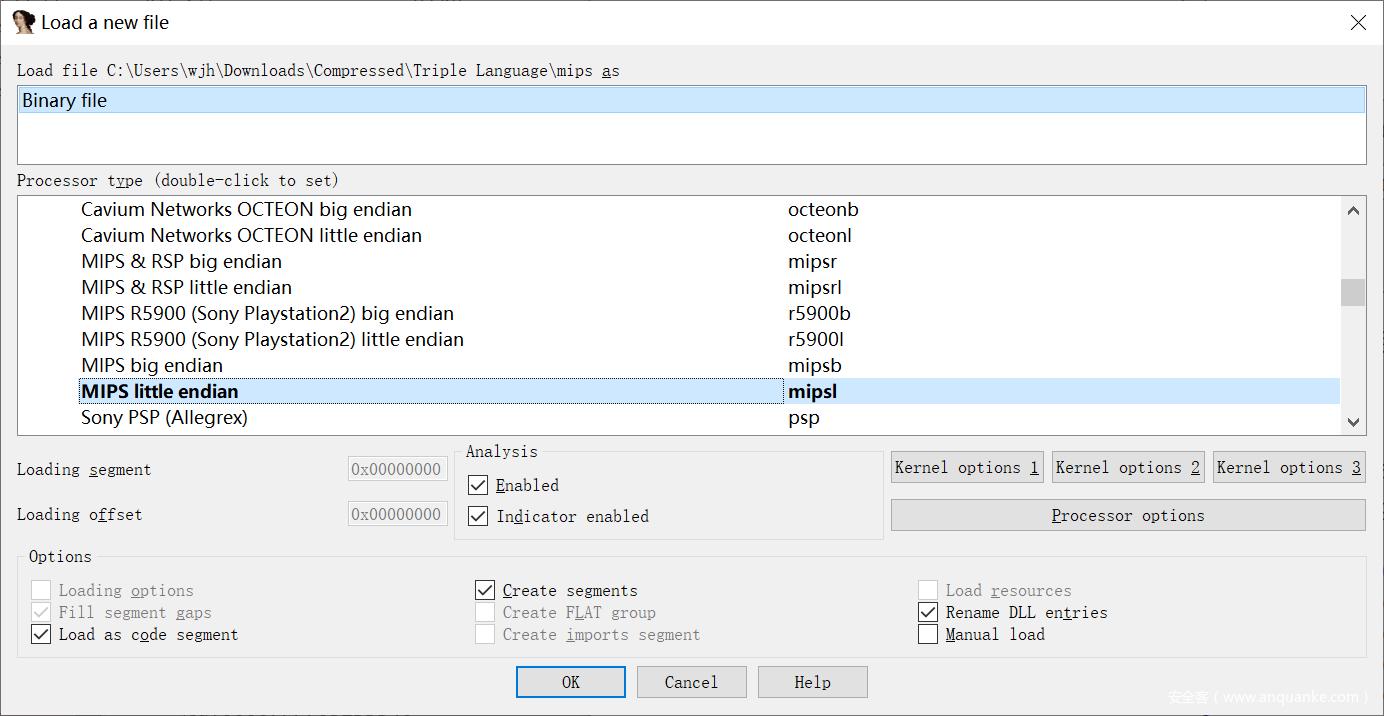
将提取得到的内容用 IDA32 再次打开,这里多次试验后,发现指令集应该是 MIPS 小端
IDA 打开后,可以根据原来代码中的调用信息来修复段信息。
uc_mem_map 在 0x10000 位置定义了一个长度为 0x200000 的可读可写可执行段,我们在 IDA 选择以下内容
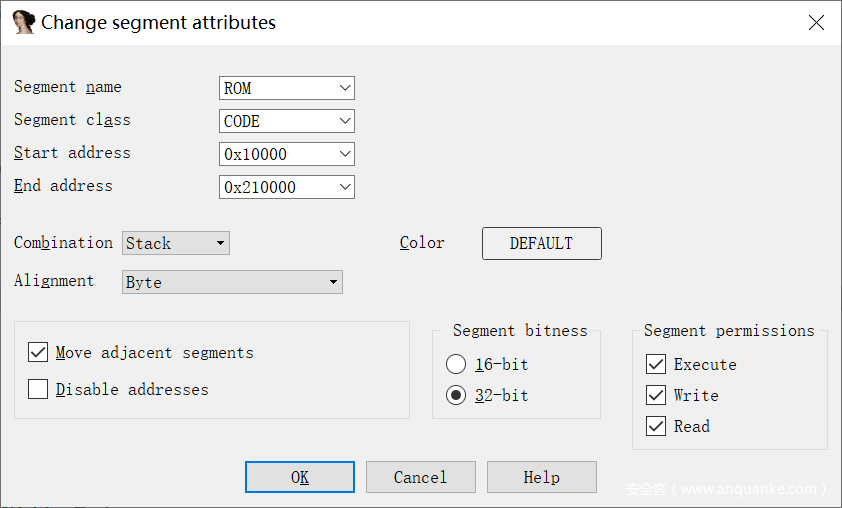
进行之后在代码内容中按 Alt +S 修改段信息,将其按照代码中的,勾选右下角三个勾
再到代码中按 C 来转为 Code
结合之前的信息,我们很容易得知这三个位置的内容分别是
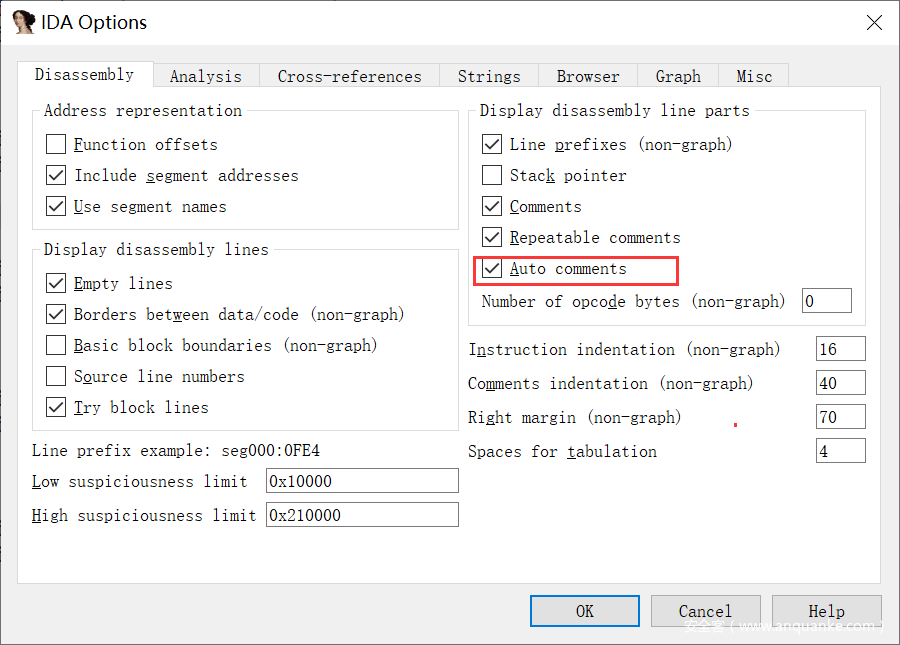
0x11000 对应一个常量,0x12000 对应从 Input[6] ~ Input[13],0x13000 对应从 Input[14] ~ Input[21],我们可以修改其命名来方便阅读,但是其中的汇编指令不太懂,并且离线无法查询,这时候可以打开 IDA 的 Auto comments
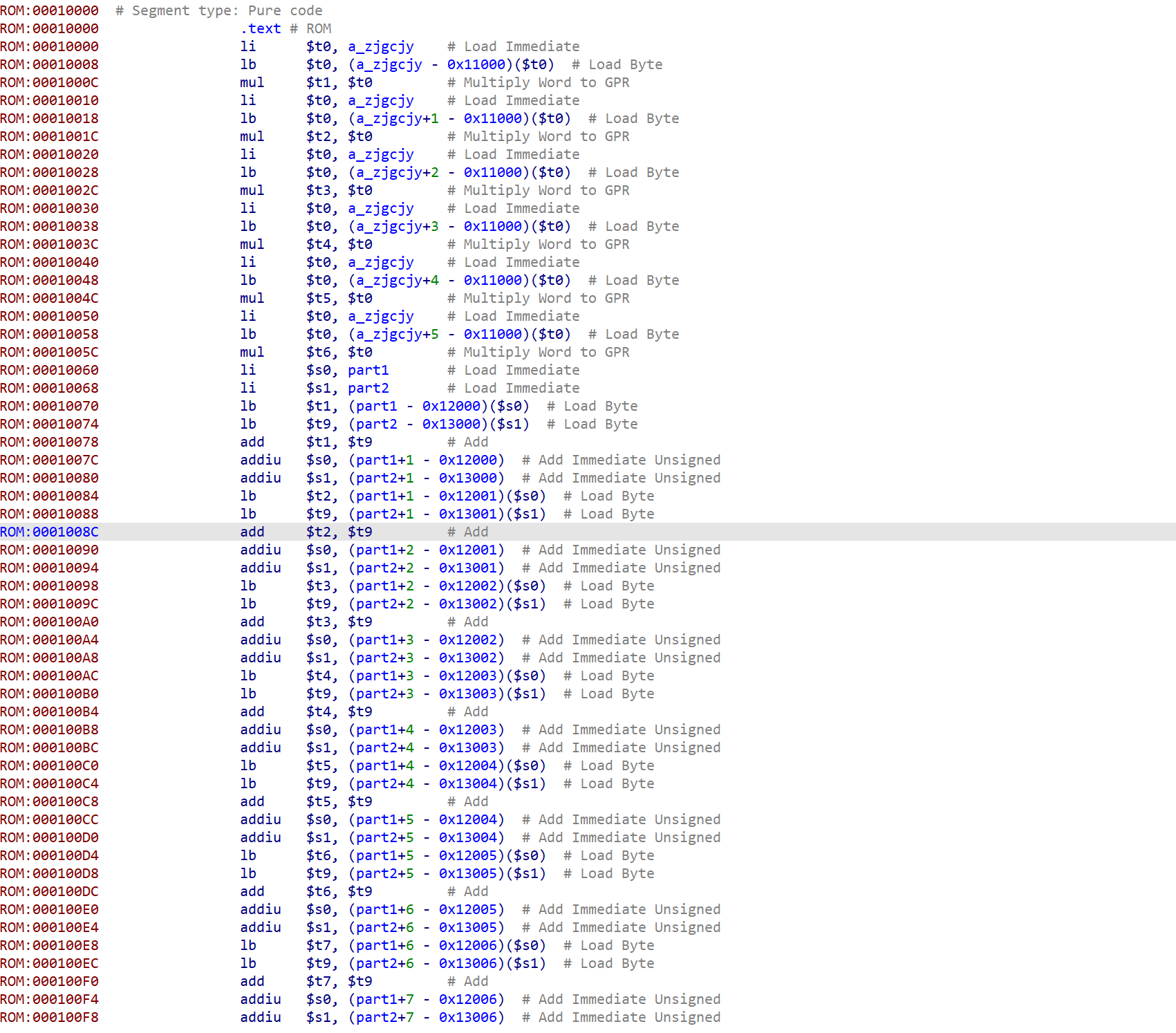
以上都修改后,代码内容为
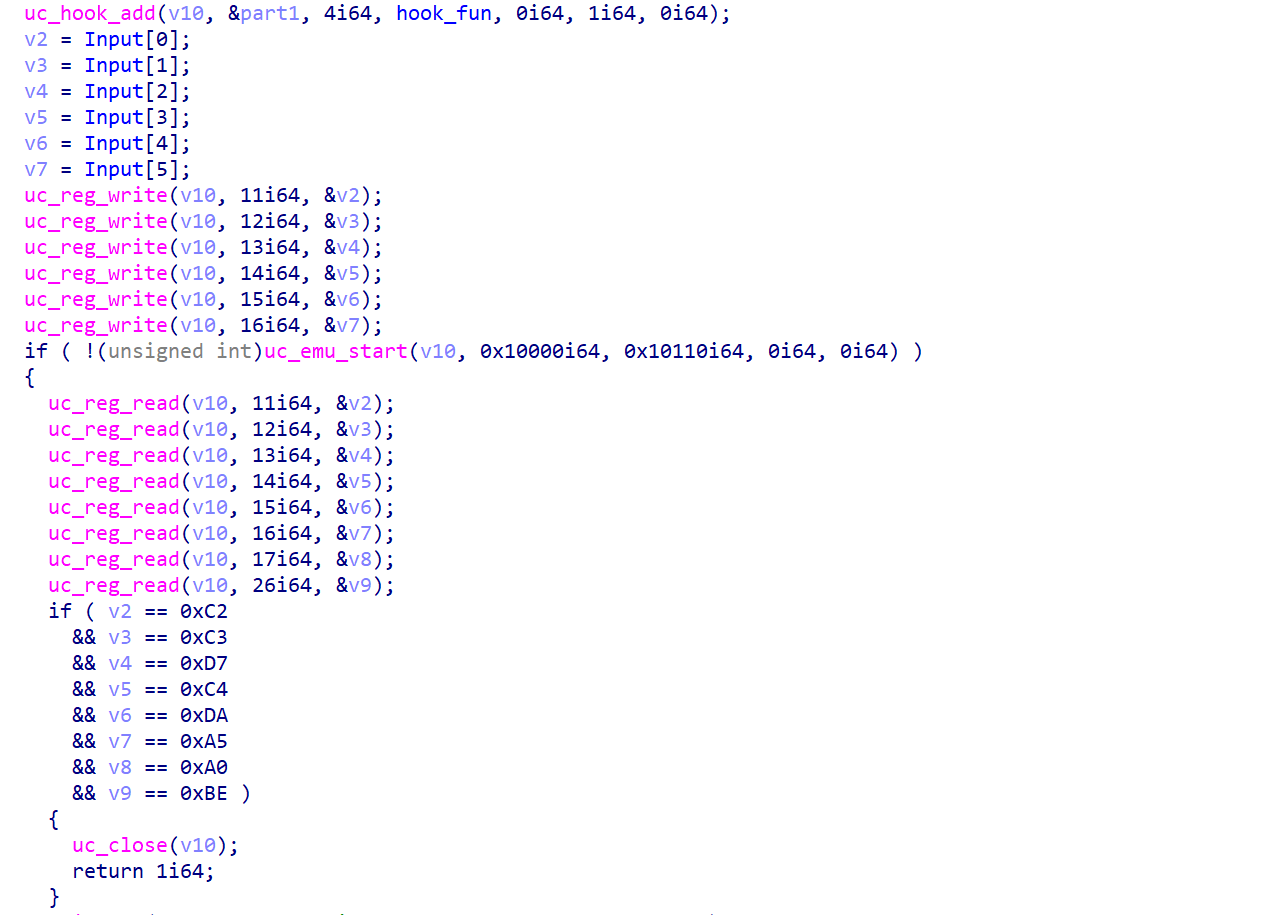
做完以上事情,是时候去看看程序 Hook 了那些内容了。
结合 Hook 的位置来对应其代码内容不难看出,实际上在验证汇编执行 mul (乘法)之后的结果,而这几个乘法的结果,取决于 t1 – t6 这六个寄存器,而这六个寄存器在启动前被赋值,值来源于输入内容的前六字节
也就是我们得到了一个关于前六字节的约束,而且这个约束是有唯一确定的结果的。
约束三
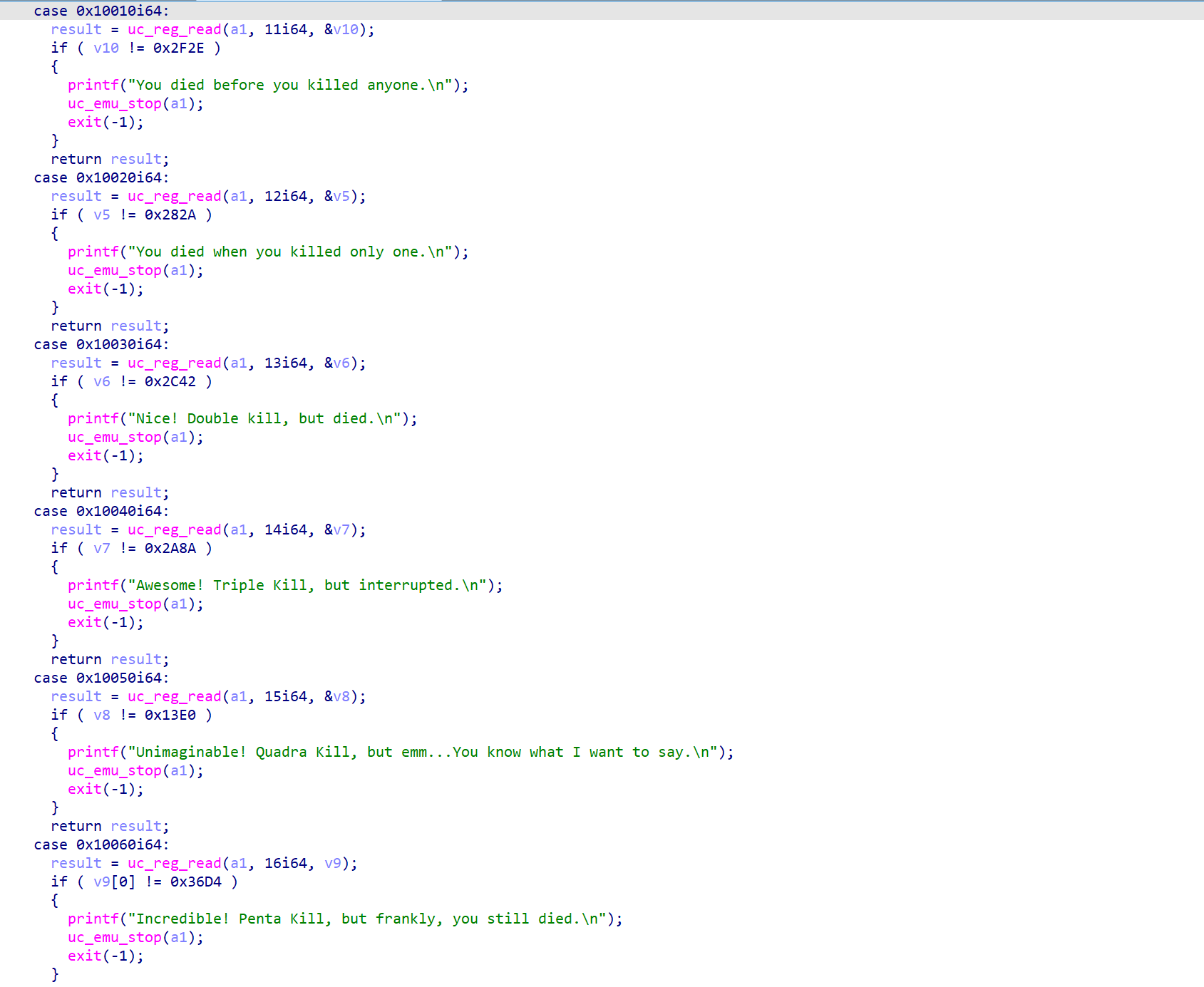
续上文,我们可以看到程序在 unicorn 结束执行后还对几个寄存器进行了比对,如果比对一致则返回 1。
结合上面的代码和注释,不难看出,这几个寄存器的加载的内容就是 part1 和 part2 中对应内容相加的值。结合上面的约束一,已知 part1 + part2 和 part1 – part2,就不难得到 part1 和 part2 的值。
Check1 解题脚本
结合以上三个约束,我们可以编写如下脚本
from z3 import *
solver = Solver()
mul = [0x2F2E, 0x282A, 0x2C42, 0X2A8A, 0x13E0, 0x36D4]
sign = "zjgcjy"
flag = ""
for i in range(len(mul)):
flag += chr(mul[i] // ord(sign[i: i + 1]))
k1 = [0x00, 0x3E, 0XBB, 0X0E, 0XFA, 0xF3, 0x01, 0xFC][::-1]
k2 = [0xC2, 0XC3, 0XD7, 0XC4, 0XDA, 0XA5, 0XA0, 0XBE]
input = [BitVec('f%d' % i, 8) for i in range(16)]
for i in range(8):
solver.add(input[i] - input[i + 8] == k1[i])
solver.add(input[i] + input[i + 8] == k2[i])
assert solver.check() == sat
ans = solver.model()
flag += ''.join([chr(ans[input[i]].as_long()) for i in range(16)])
print flag #cann0t_be_t0o_carefu1_
这个问题解决后,就准备迎来更加复杂的第二部分
第二部分
前四字节
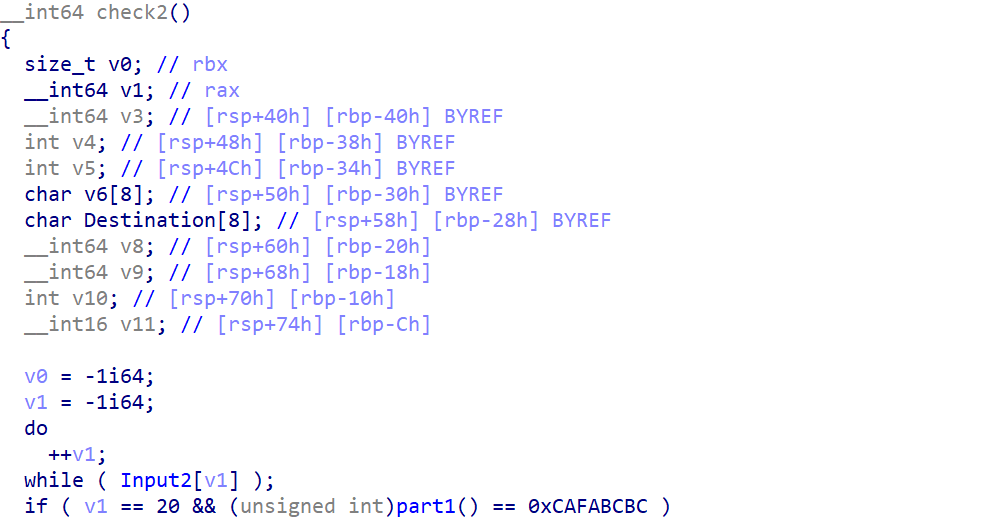
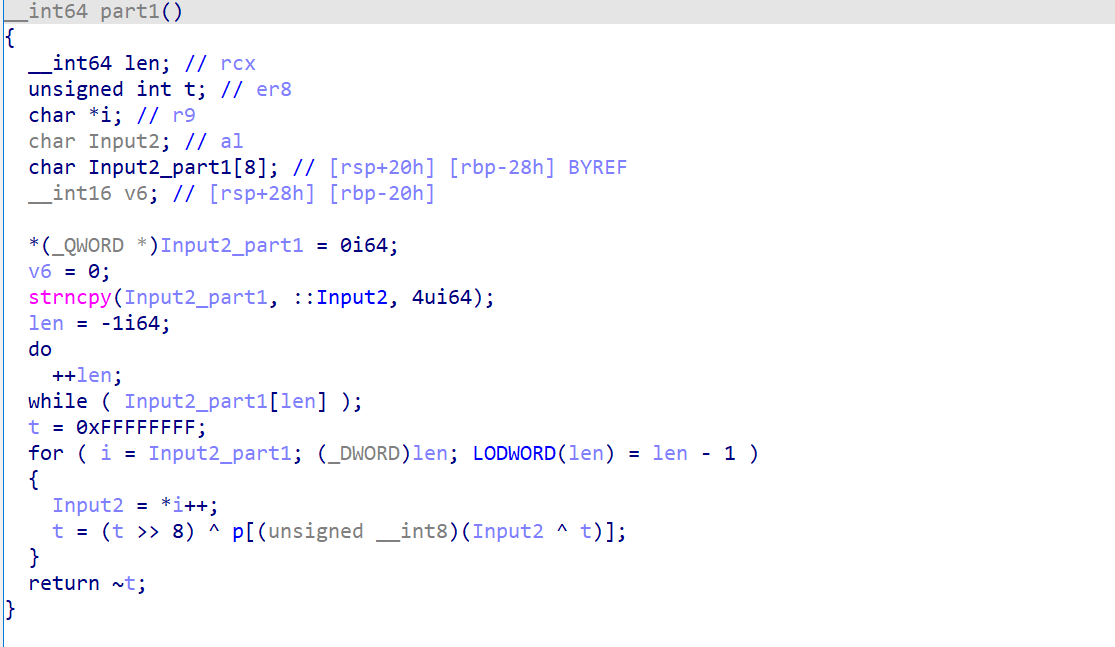
要求输入长度为 20,并且通过 part1 检测
不难看出,这部分内容实际上只检验了前四个字节,我这里给出两种做法,分别对应不同情况:
- 爆破解法:因为只有四个字节,所以在比赛过程中我考虑直接使用爆破的方法来求解,计算的时间虽然长一些,但是计算的同时我可以去看下面的代码内容。
- 如果字节数更多,那么爆破的方法就不再可行,所以赛后我又写了一份使用 Z3 来进行求解的脚本。
爆破解法
这个解法的好处在于,相比 Z3 的写法更快一些,但是要更加的注意类型约束,因为在 python 中默认是高精度的数字。
p = [0x00000000, 0xF26B8303, 0xE13B70F7, 0x1350F3F4, 0xC79A971F, 0x35F1141C, 0x26A1E7E8, 0xD4CA64EB, 0x8AD958CF, 0x78B2DBCC, 0x6BE22838, 0x9989AB3B, 0x4D43CFD0, 0xBF284CD3, 0xAC78BF27, 0x5E133C24, 0x105EC76F, 0xE235446C, 0xF165B798, 0x030E349B, 0xD7C45070, 0x25AFD373, 0x36FF2087, 0xC494A384, 0x9A879FA0, 0x68EC1CA3, 0x7BBCEF57, 0x89D76C54, 0x5D1D08BF, 0xAF768BBC, 0xBC267848, 0x4E4DFB4B, 0x20BD8EDE, 0xD2D60DDD, 0xC186FE29, 0x33ED7D2A, 0xE72719C1, 0x154C9AC2, 0x061C6936, 0xF477EA35, 0xAA64D611, 0x580F5512, 0x4B5FA6E6, 0xB93425E5, 0x6DFE410E, 0x9F95C20D, 0x8CC531F9, 0x7EAEB2FA, 0x30E349B1, 0xC288CAB2, 0xD1D83946, 0x23B3BA45, 0xF779DEAE, 0x05125DAD, 0x1642AE59, 0xE4292D5A, 0xBA3A117E, 0x4851927D, 0x5B016189, 0xA96AE28A, 0x7DA08661, 0x8FCB0562, 0x9C9BF696, 0x6EF07595, 0x417B1DBC, 0xB3109EBF, 0xA0406D4B, 0x522BEE48, 0x86E18AA3, 0x748A09A0, 0x67DAFA54, 0x95B17957, 0xCBA24573, 0x39C9C670, 0x2A993584, 0xD8F2B687, 0x0C38D26C, 0xFE53516F, 0xED03A29B, 0x1F682198, 0x5125DAD3, 0xA34E59D0, 0xB01EAA24, 0x42752927, 0x96BF4DCC, 0x64D4CECF, 0x77843D3B, 0x85EFBE38, 0xDBFC821C, 0x2997011F, 0x3AC7F2EB, 0xC8AC71E8, 0x1C661503, 0xEE0D9600, 0xFD5D65F4, 0x0F36E6F7, 0x61C69362, 0x93AD1061, 0x80FDE395, 0x72966096, 0xA65C047D, 0x5437877E, 0x4767748A, 0xB50CF789, 0xEB1FCBAD, 0x197448AE, 0x0A24BB5A, 0xF84F3859, 0x2C855CB2, 0xDEEEDFB1, 0xCDBE2C45, 0x3FD5AF46, 0x7198540D, 0x83F3D70E, 0x90A324FA, 0x62C8A7F9, 0xB602C312, 0x44694011, 0x5739B3E5, 0xA55230E6, 0xFB410CC2, 0x092A8FC1, 0x1A7A7C35, 0xE811FF36, 0x3CDB9BDD, 0xCEB018DE, 0xDDE0EB2A, 0x2F8B6829, 0x82F63B78, 0x709DB87B, 0x63CD4B8F, 0x91A6C88C, 0x456CAC67, 0xB7072F64, 0xA457DC90, 0x563C5F93, 0x082F63B7, 0xFA44E0B4, 0xE9141340, 0x1B7F9043, 0xCFB5F4A8, 0x3DDE77AB, 0x2E8E845F, 0xDCE5075C, 0x92A8FC17, 0x60C37F14, 0x73938CE0, 0x81F80FE3, 0x55326B08, 0xA759E80B, 0xB4091BFF, 0x466298FC, 0x1871A4D8, 0xEA1A27DB, 0xF94AD42F, 0x0B21572C, 0xDFEB33C7, 0x2D80B0C4, 0x3ED04330, 0xCCBBC033, 0xA24BB5A6, 0x502036A5, 0x4370C551, 0xB11B4652, 0x65D122B9, 0x97BAA1BA, 0x84EA524E, 0x7681D14D, 0x2892ED69, 0xDAF96E6A, 0xC9A99D9E, 0x3BC21E9D, 0xEF087A76, 0x1D63F975, 0x0E330A81, 0xFC588982, 0xB21572C9, 0x407EF1CA, 0x532E023E, 0xA145813D, 0x758FE5D6, 0x87E466D5, 0x94B49521, 0x66DF1622, 0x38CC2A06, 0xCAA7A905, 0xD9F75AF1, 0x2B9CD9F2, 0xFF56BD19, 0x0D3D3E1A, 0x1E6DCDEE, 0xEC064EED, 0xC38D26C4, 0x31E6A5C7, 0x22B65633, 0xD0DDD530, 0x0417B1DB, 0xF67C32D8, 0xE52CC12C, 0x1747422F, 0x49547E0B, 0xBB3FFD08, 0xA86F0EFC, 0x5A048DFF, 0x8ECEE914, 0x7CA56A17, 0x6FF599E3, 0x9D9E1AE0, 0xD3D3E1AB, 0x21B862A8, 0x32E8915C, 0xC083125F, 0x144976B4, 0xE622F5B7, 0xF5720643, 0x07198540, 0x590AB964, 0xAB613A67, 0xB831C993, 0x4A5A4A90, 0x9E902E7B, 0x6CFBAD78, 0x7FAB5E8C, 0x8DC0DD8F, 0xE330A81A, 0x115B2B19, 0x020BD8ED, 0xF0605BEE, 0x24AA3F05, 0xD6C1BC06, 0xC5914FF2, 0x37FACCF1, 0x69E9F0D5, 0x9B8273D6, 0x88D28022, 0x7AB90321, 0xAE7367CA, 0x5C18E4C9, 0x4F48173D, 0xBD23943E, 0xF36E6F75, 0x0105EC76, 0x12551F82, 0xE03E9C81, 0x34F4F86A, 0xC69F7B69, 0xD5CF889D, 0x27A40B9E, 0x79B737BA, 0x8BDCB4B9, 0x988C474D, 0x6AE7C44E, 0xBE2DA0A5, 0x4C4623A6, 0x5F16D052, 0xAD7D5351, 0xD76AA478]
allow = string.digits + string.letters
for i in allow:
for j in allow:
for k in allow:
for l in allow:
t = i + j + k + l
v1 = 0xFFFFFFFF
for x in range(4):
v1 = ((v1 >> 8) ^ p[(ord(t[x: x + 1]) ^ v1) & 0xff]) & 0xffffffff
v1 = ~v1 & 0xffffffff
if v1 == 0x0CAFABCBC:
print t #when
exit(0)
Z3 解法
这个解法速度快,效率高,但是编写过程中需要一些思考,对 Z3 能力的考察也更多一些。
p = [0x00000000, 0xF26B8303, 0xE13B70F7, 0x1350F3F4, 0xC79A971F, 0x35F1141C, 0x26A1E7E8, 0xD4CA64EB, 0x8AD958CF, 0x78B2DBCC, 0x6BE22838, 0x9989AB3B, 0x4D43CFD0, 0xBF284CD3, 0xAC78BF27, 0x5E133C24, 0x105EC76F, 0xE235446C, 0xF165B798, 0x030E349B, 0xD7C45070, 0x25AFD373, 0x36FF2087, 0xC494A384, 0x9A879FA0, 0x68EC1CA3, 0x7BBCEF57, 0x89D76C54, 0x5D1D08BF, 0xAF768BBC, 0xBC267848, 0x4E4DFB4B, 0x20BD8EDE, 0xD2D60DDD, 0xC186FE29, 0x33ED7D2A, 0xE72719C1, 0x154C9AC2, 0x061C6936, 0xF477EA35, 0xAA64D611, 0x580F5512, 0x4B5FA6E6, 0xB93425E5, 0x6DFE410E, 0x9F95C20D, 0x8CC531F9, 0x7EAEB2FA, 0x30E349B1, 0xC288CAB2, 0xD1D83946, 0x23B3BA45, 0xF779DEAE, 0x05125DAD, 0x1642AE59, 0xE4292D5A, 0xBA3A117E, 0x4851927D, 0x5B016189, 0xA96AE28A, 0x7DA08661, 0x8FCB0562, 0x9C9BF696, 0x6EF07595, 0x417B1DBC, 0xB3109EBF, 0xA0406D4B, 0x522BEE48, 0x86E18AA3, 0x748A09A0, 0x67DAFA54, 0x95B17957, 0xCBA24573, 0x39C9C670, 0x2A993584, 0xD8F2B687, 0x0C38D26C, 0xFE53516F, 0xED03A29B, 0x1F682198, 0x5125DAD3, 0xA34E59D0, 0xB01EAA24, 0x42752927, 0x96BF4DCC, 0x64D4CECF, 0x77843D3B, 0x85EFBE38, 0xDBFC821C, 0x2997011F, 0x3AC7F2EB, 0xC8AC71E8, 0x1C661503, 0xEE0D9600, 0xFD5D65F4, 0x0F36E6F7, 0x61C69362, 0x93AD1061, 0x80FDE395, 0x72966096, 0xA65C047D, 0x5437877E, 0x4767748A, 0xB50CF789, 0xEB1FCBAD, 0x197448AE, 0x0A24BB5A, 0xF84F3859, 0x2C855CB2, 0xDEEEDFB1, 0xCDBE2C45, 0x3FD5AF46, 0x7198540D, 0x83F3D70E, 0x90A324FA, 0x62C8A7F9, 0xB602C312, 0x44694011, 0x5739B3E5, 0xA55230E6, 0xFB410CC2, 0x092A8FC1, 0x1A7A7C35, 0xE811FF36, 0x3CDB9BDD, 0xCEB018DE, 0xDDE0EB2A, 0x2F8B6829, 0x82F63B78, 0x709DB87B, 0x63CD4B8F, 0x91A6C88C, 0x456CAC67, 0xB7072F64, 0xA457DC90, 0x563C5F93, 0x082F63B7, 0xFA44E0B4, 0xE9141340, 0x1B7F9043, 0xCFB5F4A8, 0x3DDE77AB, 0x2E8E845F, 0xDCE5075C, 0x92A8FC17, 0x60C37F14, 0x73938CE0, 0x81F80FE3, 0x55326B08, 0xA759E80B, 0xB4091BFF, 0x466298FC, 0x1871A4D8, 0xEA1A27DB, 0xF94AD42F, 0x0B21572C, 0xDFEB33C7, 0x2D80B0C4, 0x3ED04330, 0xCCBBC033, 0xA24BB5A6, 0x502036A5, 0x4370C551, 0xB11B4652, 0x65D122B9, 0x97BAA1BA, 0x84EA524E, 0x7681D14D, 0x2892ED69, 0xDAF96E6A, 0xC9A99D9E, 0x3BC21E9D, 0xEF087A76, 0x1D63F975, 0x0E330A81, 0xFC588982, 0xB21572C9, 0x407EF1CA, 0x532E023E, 0xA145813D, 0x758FE5D6, 0x87E466D5, 0x94B49521, 0x66DF1622, 0x38CC2A06, 0xCAA7A905, 0xD9F75AF1, 0x2B9CD9F2, 0xFF56BD19, 0x0D3D3E1A, 0x1E6DCDEE, 0xEC064EED, 0xC38D26C4, 0x31E6A5C7, 0x22B65633, 0xD0DDD530, 0x0417B1DB, 0xF67C32D8, 0xE52CC12C, 0x1747422F, 0x49547E0B, 0xBB3FFD08, 0xA86F0EFC, 0x5A048DFF, 0x8ECEE914, 0x7CA56A17, 0x6FF599E3, 0x9D9E1AE0, 0xD3D3E1AB, 0x21B862A8, 0x32E8915C, 0xC083125F, 0x144976B4, 0xE622F5B7, 0xF5720643, 0x07198540, 0x590AB964, 0xAB613A67, 0xB831C993, 0x4A5A4A90, 0x9E902E7B, 0x6CFBAD78, 0x7FAB5E8C, 0x8DC0DD8F, 0xE330A81A, 0x115B2B19, 0x020BD8ED, 0xF0605BEE, 0x24AA3F05, 0xD6C1BC06, 0xC5914FF2, 0x37FACCF1, 0x69E9F0D5, 0x9B8273D6, 0x88D28022, 0x7AB90321, 0xAE7367CA, 0x5C18E4C9, 0x4F48173D, 0xBD23943E, 0xF36E6F75, 0x0105EC76, 0x12551F82, 0xE03E9C81, 0x34F4F86A, 0xC69F7B69, 0xD5CF889D, 0x27A40B9E, 0x79B737BA, 0x8BDCB4B9, 0x988C474D, 0x6AE7C44E, 0xBE2DA0A5, 0x4C4623A6, 0x5F16D052, 0xAD7D5351, 0xD76AA478]
a = Array('a', BitVecSort(32), BitVecSort(32))
for i in range(256):
solver.add(a[i] == p[i])
Input = [BitVec('Input%d' % i, 8) for i in range(4)]
t = BitVec('v1', 32)
solver.add(t == 0xFFFFFFFF)
for i in range(4):
idx = (ZeroExt(24, Input[i]) ^ t) & 0xff
t = LShR(t, 8) ^ a[idx]
t = ~t
solver.add(t == 0x0CAFABCBC)
assert solver.check() == sat
ans = solver.model()
print ''.join([chr(ans[Input[i]].as_long()) for i in range(4)]) #when
这个解法速度快,效率高,但是编写过程中需要一些思考,对 Z3 能力的考察也更多一些。
其余字节
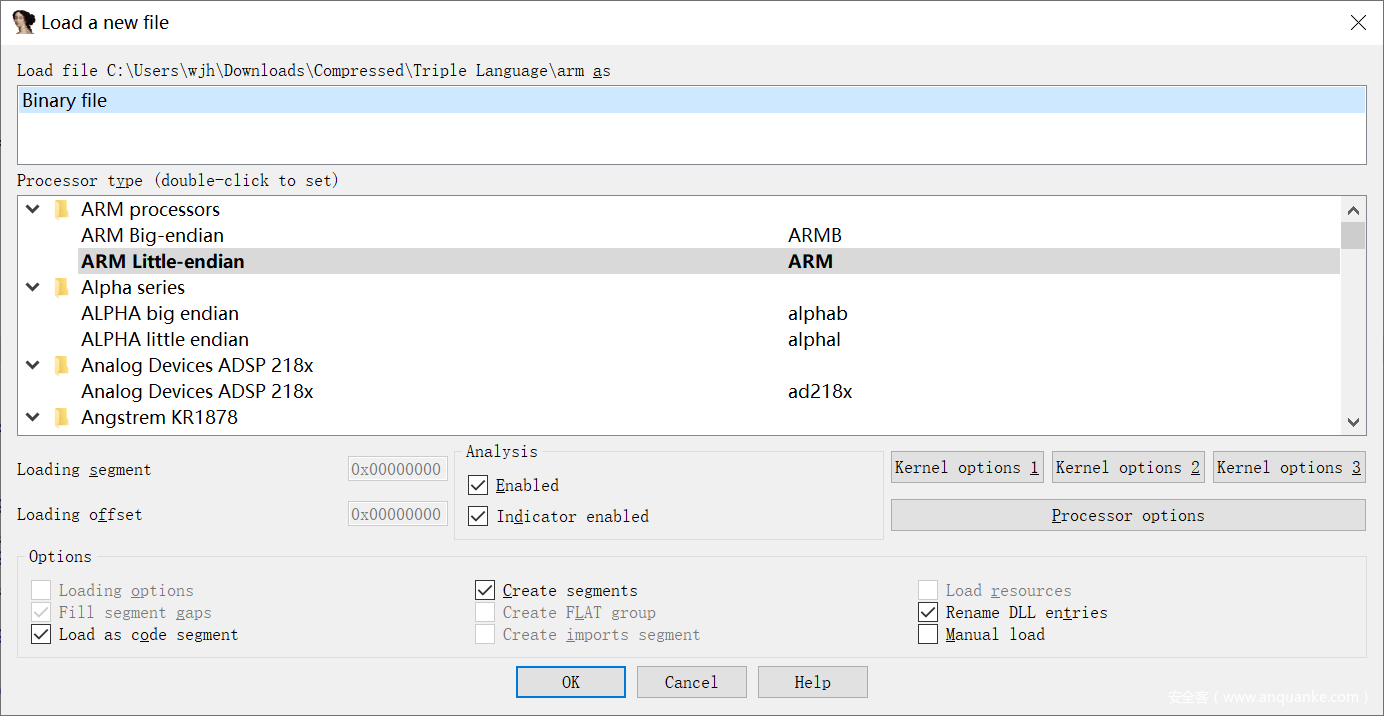
结合上面的分析方法,得知这个代码架构是 ARM·
导出代码然后用 IDA 打开
打开后设置
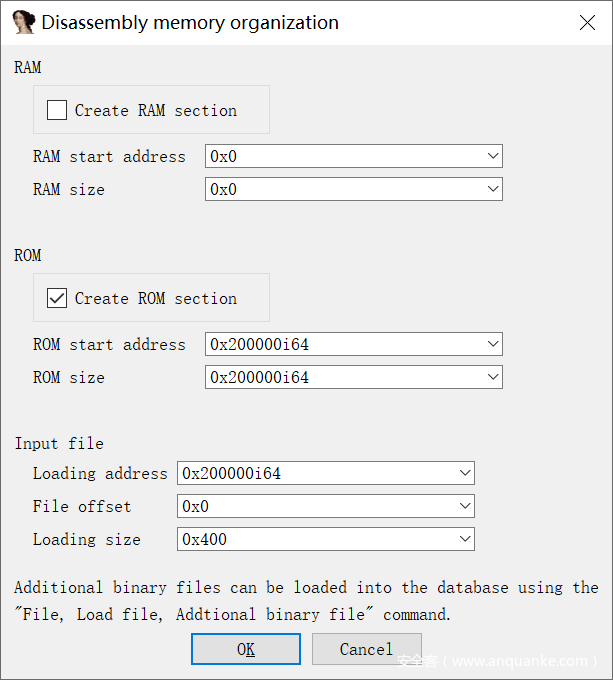
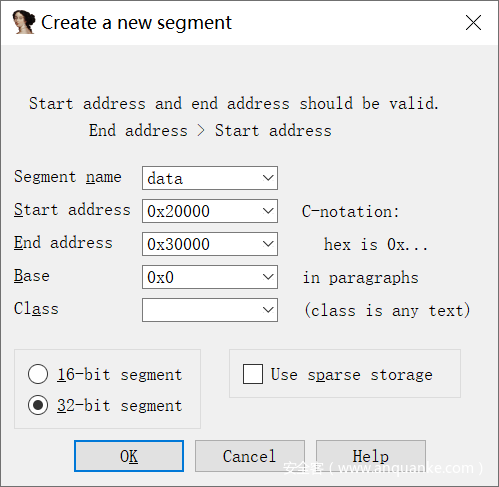
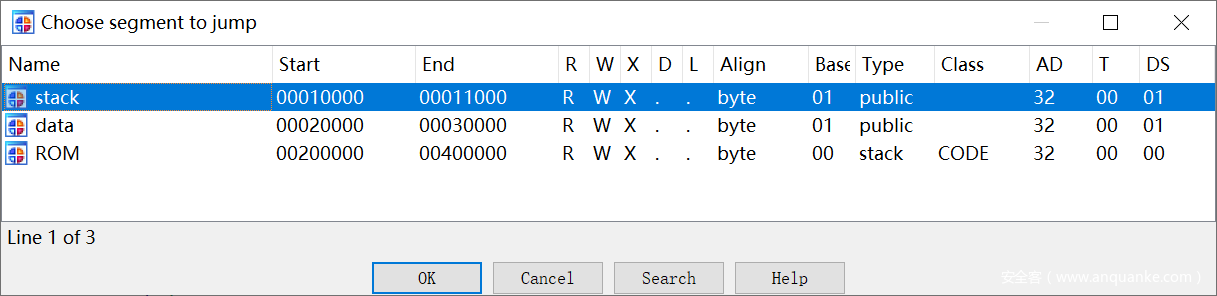
根据代码中 uc_mem_map 的内容可以添加几个段,名称可以随意取
[1]0x10000 开始,长度为 0x1000
[2]0x20000 开始,长度为 0x10000
再分别给上面三个段开 RWX,便于 IDA 识别
这时候,在 ROM 段框选全部的代码内容,再按 P 可以生成函数,按 F5 也可以查看伪代码,但是由于没有给变量位置定义,IDA 也没能自动识别出,这时的伪代码是不易理解的。
我们知道 0x21024 指针指向的就是我们输入内容的其余字节,所以我们可以去这个地址来定义一个变量。
按 G 可以跳转到这个地址,再按 N 可以定义一个名字
按小键盘上的 * 可以设置数组长度,这里设置为 0x1D
按 Y 可以设置变量类型,设置为 unsigned char
这时候再重新定义(点击函数头部,先按 U 取消定义,再选择整个函数的代码内容按 P 定义函数)这个函数,效果就完全不同了
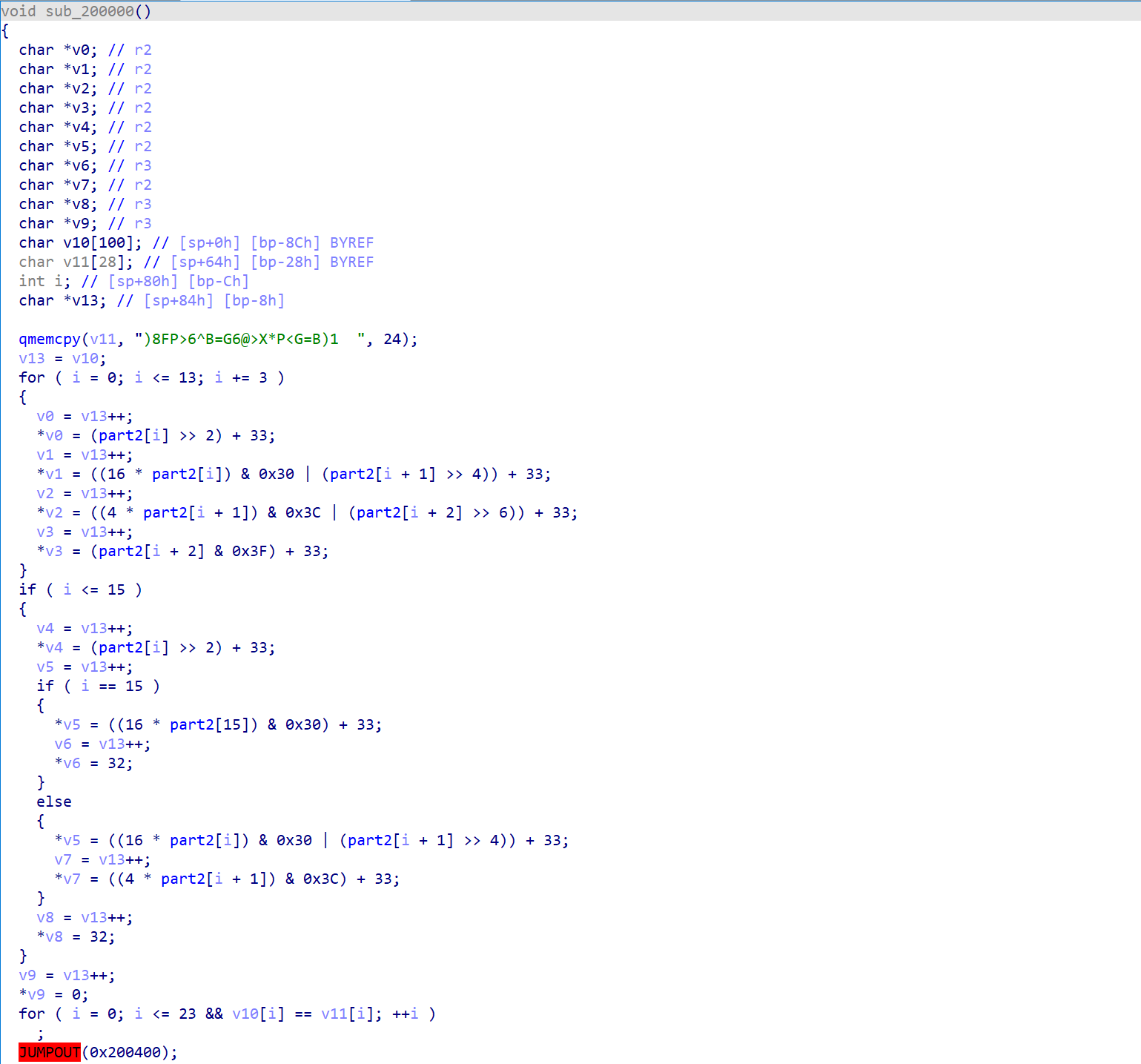
代码的含义已经是比较清晰了
接下来来看看 hook 函数的代码,它对于 R3(0x45 常量对应)寄存器的内容进行了修改,使得最终结果不同,反应到伪代码上的内容就是上图中的 v11 变量的内容。
所以我们可以考虑先把这些变化依次在汇编中注释,然后再还原。
Z3 解题代码
from z3 import *
en = [0x29 + 15, 0x38 ^ 0x6f, 0x46 - 12, 0x50 ^ 0x12, 0x3E - 5, 0x36 + 33, 0x5E - 12, 0x42 ^ 0xd, 0x3D - 3, 0x47 + 15,
0x36 ^ 0x68, 0x40 ^ 0xA, 0x3E - 5, 0x58 - 33, 0x2A + 48, 0x50 ^ 0x18, 0x3C + 2, 0x47 - 16, 0x3D ^ 0x1B, 0x42 + 6,
0x29 ^ 0x13, 0x31, 0x20, 0x20]
solver = Solver()
part2 = [BitVec('part2[%d]' % i, 8) for i in range(16)]
index = -1
i = 0
for i in range(0, 13, 3):
index += 1
solver.add(((part2[i] >> 2) + 33) == en[index])
index += 1
solver.add((((16 * part2[i]) & 0x30 | (part2[i + 1] >> 4)) + 33) == en[index])
index += 1
solver.add((((4 * part2[i + 1]) & 0x3C | (part2[i + 2] >> 6)) + 33) == en[index])
index += 1
solver.add(((part2[i + 2] & 0x3F) + 33) == en[index])
i = 15
if i <= 15:
index += 1
solver.add(((part2[i] >> 2) + 33) == en[index])
index += 1
if i == 15:
solver.add((((16 * part2[i]) & 0x30) + 33) == en[index])
index += 1
solver.add(0x20 == en[index])
else:
solver.add((((16 * part2[i]) & 0x30 | (part2[i + 1] >> 4)) + 33) == en[index])
index += 1
solver.add((((4 * part2[i + 1]) & 0x3C) + 33) == en[index])
index += 1
solver.add(0x20 == en[index])
assert solver.check() == sat
ans = solver.model()
print ''.join([chr(ans[part2[i]].as_long()) for i in range(16)]) #_faclng_ianguage
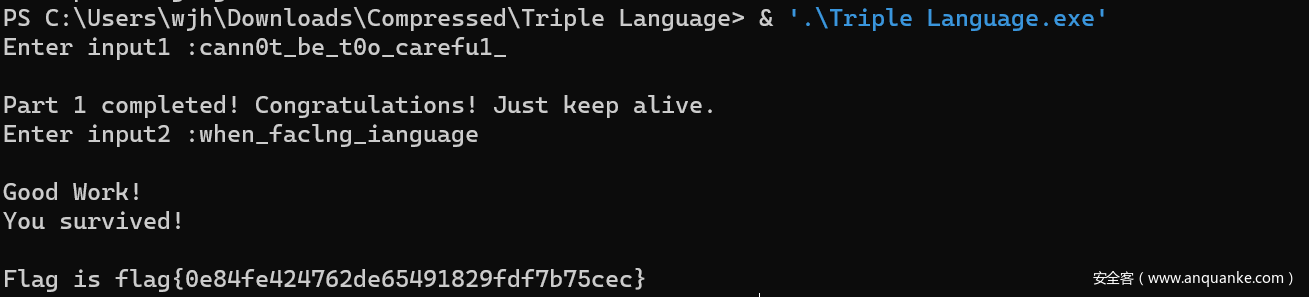
GetFlag
总结
我认为这题非常值得大家学习,我认为以后也会出现类似的赛题,如果提前熟悉 unicorn,那么做题速度一定会大大的增加,但是这道题目对于这个比赛实在是不太友好,而且在比赛进行到一半时间才把附件放出,导致大多数选手没能完成本题,且在比赛过程中不能使用外网,对于一些并没有接触过 unicorn 的同学来说,这题里的一些函数调用,包括一些常数的定义,以及 MIPS 汇编、ARM 汇编的含义也难以理解。
题目文件
链接: https://pan.baidu.com/s/1OqoBwt1_uHu0Z0vgOw4Xaw 提取码: 6grn


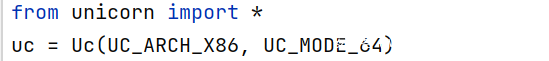



















发表评论
您还未登录,请先登录。
登录