一、简介
现有 fuzz 大多以代码覆盖率为引导指标。以AFL为例,它使用映射至 hashmap 中的基于 edge 的覆盖率信息来引导测试。这种覆盖率信息不太准确,因为只统计至 edge 层面,同时还会产生覆盖 hash 冲突,丢失覆盖率信息,给模糊测试带来一些不良限制。
这篇论文提出了一个新的方式,来达到以下三个目的:
- 提供更准确的覆盖信息
- 缓解路径冲突
- 保持较低检测开销
同时,该论文还利用覆盖率信息,提出了三种新的模糊测试策略,加快了发现新路径和漏洞的速度。
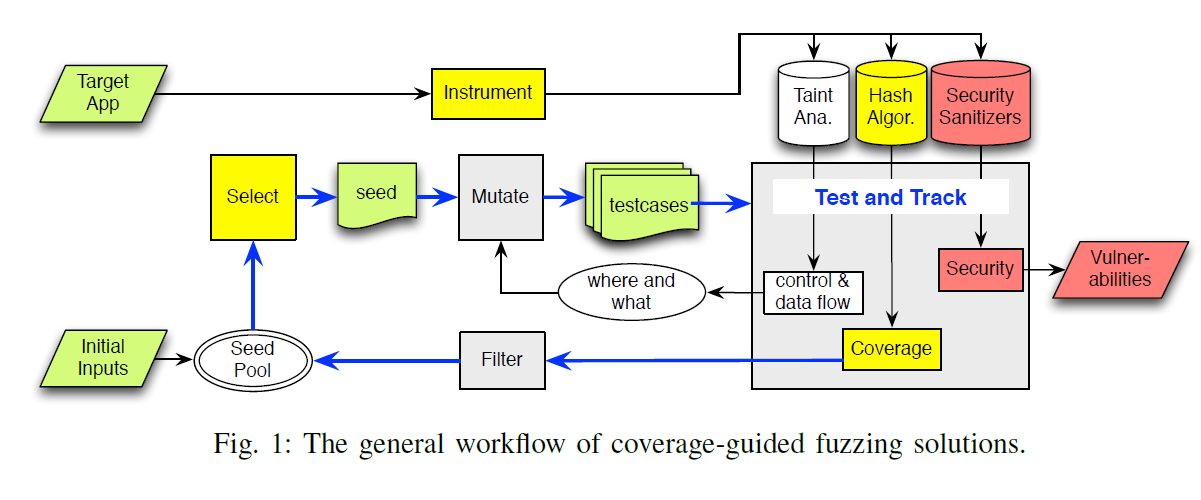
下图是一个完整 fuzz 的工作流程,其中黄色标注部分为论文所提出的重点思路:
二、降低哈希碰撞策略
1. 覆盖粒度
覆盖粒度大体上可分为三类:
- block coverage,块覆盖
- edge coverage,边覆盖
- path coverage,路径覆盖
每种粒度各有利弊:
- 块覆盖:跟踪每个块的命中次数,但不跟踪块的执行顺序。
- 边覆盖:与块覆盖不同,它将跟踪两个块之间的执行顺序。同时,还跟踪每条边的命中次数,但不跟踪边的执行顺序。
- 路径覆盖:跟踪边的执行顺序,提供最完整的覆盖信息。但是,受限于路径长度和路径数量的规模之大,跟踪路径覆盖信息将会导致开销非常高,因此不具有可行性。
综上,边覆盖信息在可行性与覆盖信息之间做了一个折中。但以 AFL 为例,边覆盖信息仍然可能会受到哈希碰撞的影响而导致信息丢失。即便提高 bitmap 的大小,但这仍然无法避免哈希碰撞,并且会对 AFL 的运行带来严重性能开销(因为 AFL 会经常遍历 bitmap 以获取新的覆盖率信息)。
因此接下来将说明 CollAFL 的做法,它将降低哈希碰撞问题发生的影响。
2. 降低哈希碰撞
先简单回忆一下 AFL 的 hash 计算方式:$cur \oplus (prev>>1)$。
其中 cur 和 prev 为当前和上一个基础块的 ID。
对 prev 做了一个右移操作是为了区分开基础块 A->B 和 B->A 的差别。
具体的内容可以看看我之前做的笔记 AFL的LLVM_Mode。
而 CollAFL 在原先 AFL 的 hash 计算方式上做了一些改进,它插入了一个三元组 (x,y,z) 作为 hash 计算参数(下称参数)。
边 A-> B 的 hash 计算方程为:$Fmul(cur, prev) = (cur >> x) \oplus (prev >> y) + z$。
其中 AFL hash algorithm 是 (x=0,y=1,z=0) 的一个特例。
从这也可以看出,Fmul 的计算开销与 AFL 差不多。
需要注意的是,CollAFL 为每个基本块来选择参数,而不是为边选择参数。
CollAFL 将通过调整参数,来确保每个通过 Fmul 方程计算出的边的 hash 是不同的。若每个基本块中使用的参数均可以使得每条边的 hash 不同,那么就可以解决 hash 碰撞问题。
但需要注意的是,由于应用程序的基本块过多,因此无法遍历全部的基本块,同时也无法遍历全部的参数。因此实际上 CollAFL 在这个方程的基础之上又做了一些改进,根据以下几种不同的情况,来分别进行不同的操作,以降低 hash 碰撞的概率。
a. 基本块有多个前驱基本块
1) CalcFmul
初始时,CollAFL 将使用上述 Fmul 方程,动态计算入边的 hash。以下是 collAFL 贪心搜索合适的参数以计算 Fmul 方程的算法:
输入参数是
- 具有多个前驱基本块的目标基本块集合
- 基本块与基本块 ID 的映射关系
- 每个目标基本块的前驱基本块集合
如果部分基本块,在有限的 xyz 参数集合中无法找到不会哈希碰撞的参数后,那么该基本块将被放入 Unsolve 集合中;如果能搜索到合适的参数,则目标基本块将放入 Solve 集合中,且搜索到的参数放入 Params 映射里。
最终,calcFmul 函数将输出以下四个:
- 已经解决的基本块集合 Solv
- 尚未解决的基本块集合 Unsol
- 已经解决的基本块集合与参数的映射关系 Params:$BacicBlock \to <x,y,z>$
- 此时的 hash 表
需要注意的是 Fmul 无法保证通过选择适当的参数来达到防止任何哈希冲突,因此 calcFmul 算法会将可能导致哈希碰撞的基本块单独保存,并使用其他方式处理。calcFmul 能保证的是,calcFmul 解决的基本块中不会产生任何哈希碰撞。
Fmul 的哈希值必须在运行时计算得出。
2) CalcFhash
接下来,collAFL 将会处理那些通过 calcFmul 算法求解后会产生哈希碰撞的基本块。对于这些无法通过 $Fmul$ 方程解决的基本块,其新的 hash 将被称为 $Fhash$,Fhash 的获取算法如下所示:
可以看到,对于这些剩余未解决的基本块来说,随机给每个基本块的每个入边分配一个 hash 值,即是 Fhash 的求解方式。求解完成后,输出此时的哈希表以及剩余尚未分配完成的哈希。
之后,在运行时,Fhash 的值便可以通过查询先前生成的 HaspMap 表得到:$Fhash(cur, prev) = hash_table_lookup(cur, prev)$。
由于哈希表的查找比 Fmul 的算数计算慢的多,因此 Unsol 集合里的基本块数量必须尽可能地小。
b. 基本块只有一个前驱基本块
若当前遍历到的基本块只有一个基本块,则在该边的结束块中,直接为该边分配一个不与其他 hash 冲突的新 hash 值:$Fsingle(cur, prev) = c$,其中 c 是一个与其他 hash 不同的常量。
这里的 hash 分配,将在给其他基础块计算完 Fmul 和 Fhash 后再来执行,以尽可能地避免哈希碰撞。
由于这里的哈希分配与运行时的基本块前后信息无关(因为此时基本块只有一个前驱基本块),因此可以直接在插桩时便硬编码进入,无需运行时再计算 hash。
由于有大概 60% 以上的基本块只有一条前驱边,因此这样的 hash 分配将会节省 fuzz 的很多开销。
c. 整体解决方案
首先。确保哈希值空间大小大于边的数量,否则将无法避免哈希碰撞。
之后,根据上面所介绍的算法与步骤,执行以下操作:
3. 开销分析
不同哈希算法的开销如下:$cost(Fhash) > cost(Fmul) > cost(Fsingle) \approx 0$
其中,根据经验所示,大部分基础块都只有一个入边,并且 unsol 基础块的数量非常的少:
$num(Fsingle) > num(Fmul) >> num(Fhash) \approx 0$
因此,整体上 collAFL 降低哈希碰撞的方式的实用性是比较高的。
4. 对间接调用的处理
受限于静态分析的精度,一些被间接调用的基本块,可能会被错误归类为只有单个或者没有前驱基本块,影响实际使用效果。
即被间接调用的基本块,可能在调用图上没有明显的调用入边。
因此实际实现时,CollAFL 将会把没有被任何调用点直接调用的函数入口,标记为有多个前驱基本块的入口基本块,即按照有多个前驱基本块的方式(Fmul + Fhash)来计算 hash,强制不走 Fsingle 的这条路。
同时,CollAFL 还会将多个间接调用指令,展开为直接调用指令集合和一条间接调用指令,与 gcc 中的去虚拟化技术类似。
gcc 的去虚拟化技术,指的是通过一系列的分析,最终将一些不确定的虚拟调用点,与确定的虚函数绑定,从而转化成了普通的直接函数调用,去除了间接虚拟调用。
经过上述两步操作后,CollAFL将会减少那些 被识别为只有单个前驱基本块(或没有前驱基本块)的基本块数量。
CollAFL 的哈希碰撞降低技术只确保消除已知边的碰撞,因此受限于静态分析技术,仍然可能存在哈希碰撞。
三、种子变异策略
该论文提出了以下种子变异观点:
- 如果某条路径有许多未探索过的相邻分支,或者未探索过的相邻后继节点,则该路径的变异可能可以探索出新的路径
- 如果某条路径上存在较多内存访问操作,则该路径有一定概率来触发潜在内存漏洞,而对该路径的突变也有可能触发漏洞。
并根据上述观点,给出三个评估种子权重的方程:
- 探索未探索过的相邻分支策略:
Weight_Br(T) = \sum_{bb\in Path(T) \and <bb, bb_i>\in EDGES}IsUntouched(<bb, bb_i>)
- 探索未探索过的相邻后继节点策略:
Weight_Desc(T)=\sum_{bb\in Path(T) \and IsUntouched(<bb, bb_i>)} NumDesc(bb_i)
NumDesc(bb) = \sum_{<bb, bb_i>\in EDGES} NumDesc(bb_i)
- 探索存在较多内存访问操作的节点策略:
Weight_Mem(T) = \sum_{bb\in Path(T)} NumMemInstr(bb)
四、评估
评估分为两部分,分别是评估 CollAFL 降低哈希碰撞策略的效果,以及种子变异策略的效果。
1. 降低哈希碰撞
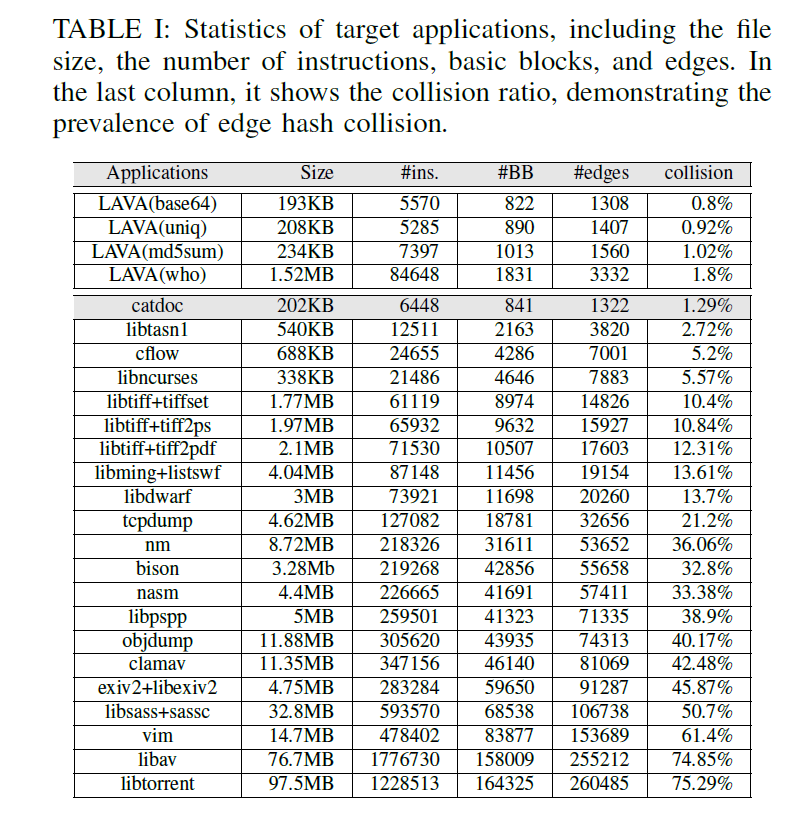
首先给出 AFL fuzz 不同项目的哈希碰撞效果,可以看到,碰撞比率还是比较高的:
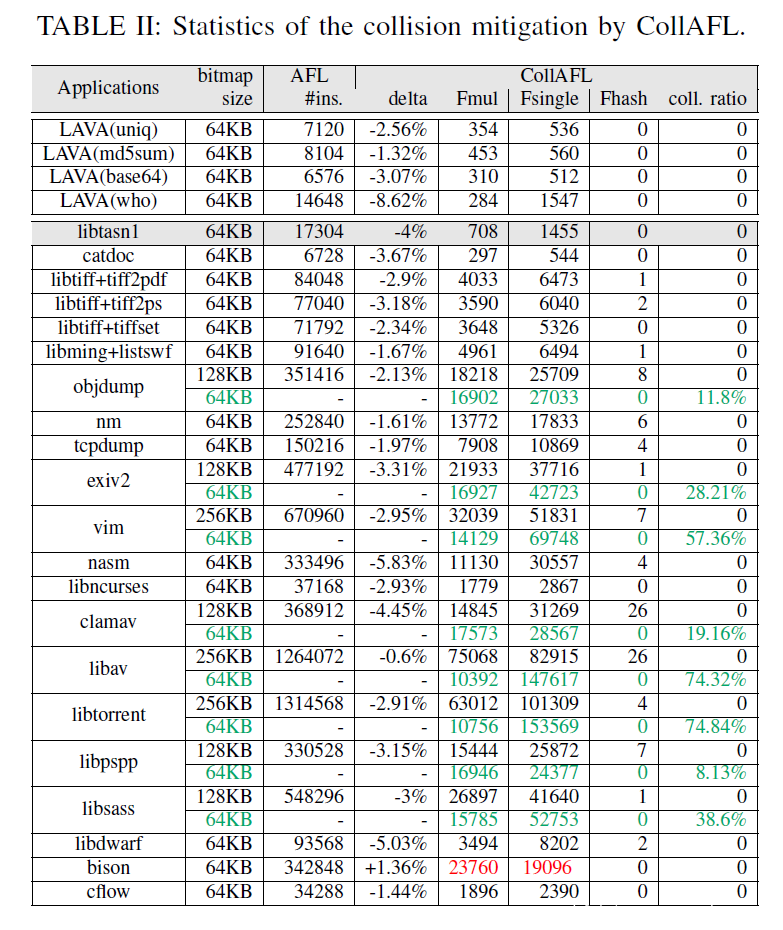
接下来再给出 CollAFL 哈希的效果,可以看到相比于 AFL,CollAFL 更好的利用了哈希空间,极大的降低了碰撞比率:
2. 种子变异
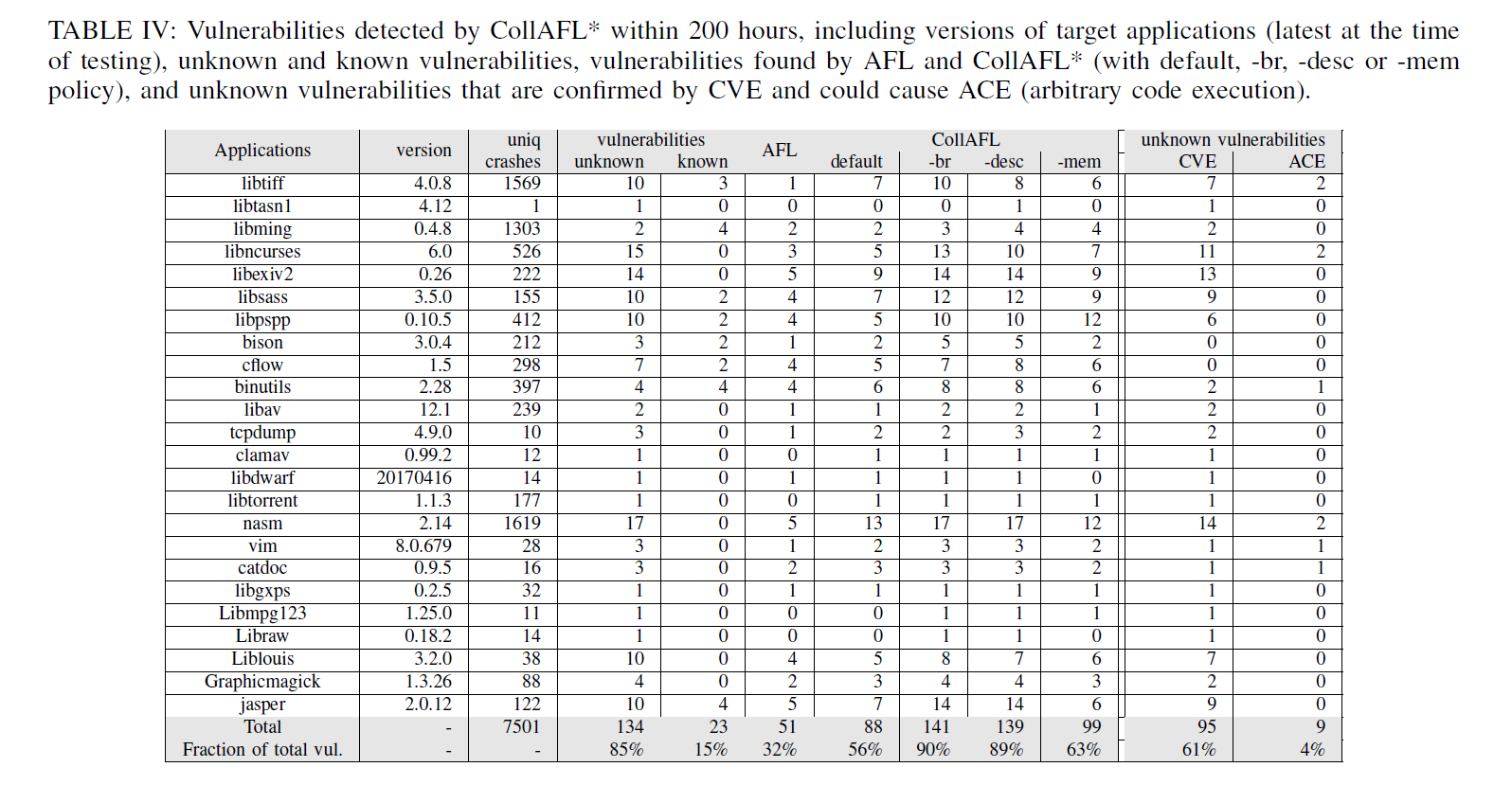
这是 CollAFL 分别使用三种种子变异策略运行200小时后的效果:
可以看到,这三种变异策略均跑出了更多的 crash,取得了不错的效果。











发表评论
您还未登录,请先登录。
登录