前言
在成员推理攻击中,攻击者训练一个二分类器,该分类器将目标分类器预测的数据样本的置信度分数向量作为输入,预测该数据样本是目标分类器训练数据集的成员数据还是非成员数据。成员推理攻击会对机器学习造成严重的隐私和安全威胁,尤其是在训练数据集敏感的应用场景中(例如,生物医学记录和位置跟踪),成功的成员推理会导致严重危害。比如如果攻击者知道受害者的数据被用来训练医疗诊断分类器,那么攻击者就可以直接推断受害者的健康状况。除了隐私之外,成员推理还会损害模型提供者的训练数据集的知识产权,因为收集和标记训练数据集可能需要大量的资源。
所以研究人员对该领域的防御展开了研究,本文会分析及复现借助对抗样本的思想来对成员推理攻击进行防御的工作,其发表于信息安全四大之一的CCS 2019,题为《MemGuard: Defending against Black-Box Membership Inference Attacks via Adversarial Examples》
防御方案分为两步,第一步MemGuard会找到一个精心设计的噪声向量,将置信度向量视为一个对抗样本。防御者会自己先训练一个防御分类器进行成员推理攻击,并基于自己的分类器构造噪声向量。由于对抗样本的可迁移性,误导防守分类器的噪声向量很可能也会误导攻击分类器。不过已有的对抗样本生成算法不足以解决我们面临的场景,因为它们没有考虑唯一的约束,即效用损失的置信度分数向量(因为噪声越大,则效用越低)。更具体地说,噪声置信度向量不应该改变查询数据样本的预测标签,仍然应该是一个概率分布。为了解决这一难题,研究人员设计了一种新的算法来寻找满足效用损失约束的小噪声向量。在第二阶段,MemGuard将之前找到的噪声向量以一定概率加入到真实置信度分数向量中,研究人员将这个概率表述为解决一个优化问题,并推导出优化问题的解析解。
前置背景
在我们设置的场景下,共有三方参与,分别是模型提供者、模型攻击者和模型防御者。
模型提供者
模型提供者会训练一个模型,然后发布出去,用户要使用时,输入查询样本,输出为一个置信度分数向量。即:
这里f代表分类器的决策函数,x是待查询的数据样本,s是置信度分数向量。置信度分数向量实际上是待查询的样本的标签的后验概率分布,比如sj就是样本标签为j的后验概率,而样本究竟被分类器分类为什么,取决于最大置信度分数,也就是
由于本文会涉及两种分类器,我们把现在讨论的,由模型提供者提供的分类器叫做目标分类器。
攻击者
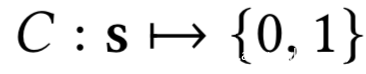
攻击者的目的是推断模型提供者的所使用的训练集。攻击者对于目标分类器只有黑盒权限,也就是说攻击者可以发送样本进行查询,得到分类器返回的置信度分数向量,通过黑盒形式的成员推理攻击来推理训练集的成员数据。在成员推理攻击中,攻击者训练一个二元分类器,它以样本的置信度向量为输入,然后会预测样本是否在目标分类器的训练集中,即:
其中C是攻击者训练的二元分类器,s是由目标分类器为查询样本x返回的置信度分数向量。如果是0,表示x不是成员数据,如果是1,表示是成员数据。我们把这里讨论的二元分类器叫做攻击分类器。
防御者
防御者的目的是防御成员推挤攻击,对于来自任何用户的任何查询样本,目标分类器会预测得到置信度分数向量,而防御者则会在将其返回给用户之前向置信度分数向量添加噪声向量,即:
其中s是目标分类器返回的真实置信度分数向量,n是防御者添加的噪声向量,s‘是返回给用户的带噪声置信分数向量。也就是说,此时攻击者只能接触到带噪声置信分数向量。而防御者添加噪声向量有两个目的:
1.攻击分类器在进行成员推理攻击时会失效,这样的话防御者就可以保护数据隐私
2.置信度分数向量的效用损失是有界的,即确保不会添加过多噪声以至于目标分类器的预测完全是不可用的。
为了实现目标1,这里还存在一些困难。首先防御者是不知道攻击者的攻击分类器的,所以防御者需要自己训练一个可以进行成员推理攻击的二元分类器,并将噪声向量添加到置信度分数向量中,来验证是否可以使二元分类器失效。这里讨论的分类器我们叫做防御分类器,将其决策函数表示为g。g(s)则表示相应样本为成员数据的概率,该样本由目标分类器返回的置信度分数向量为s。我们设防御者训练的分类器其输出层有sigmoid激活函数,这样的话决策函数的输出就代表了成员数据的概率,即:
当g(s)>0.5时,表示防御分类器认为该查询样本为成员数据。
我们设防御者采用随机噪声添加机制M,给定真实置信度分数向量s,防御者会从概率M(n|s)的可能的噪声空间中采样噪声向量n。由于随机噪声被添加到了真实置信度分数向量上,所以决策函数g会输出样本为成员数据的随机概率。防御者的目标是让g预测的概率接近0.5,也就是在加上噪声后,防御分类器会随机猜测是否为成员数据,所以防御者的目标就是找到一种机制M,可以使下式最小化
为了实现目标2,关键需要考虑该如何量化置信度分数向量的效用损失,为此引入两个效用损失指标,分别是标签损失以及置信度分数失真
标签损失:我们知道,样本的标签被预测为具有最大置信度分数的标签,如果真实置信度向量和噪声置信度向量都能使样本被预测为相同的标签,则我们说此时的标签损失为0,否则为1。很明显,我们的目标是实现0标签损失,即噪声的添加不会改变查询样本的预测标签,即满足:
置信度分数失真:查询样本的置信度向量可以告诉用户关于样本的更多信息,而不仅仅是预测标签。因此我们添加的噪声不应该使置信度分数向量有极大的失真。首先,噪声置信度向量仍然应该是一个概率分布,即满足
此外,真实置信度向量与噪声置信度向量之间的距离d(s,s+n)应该较小,我们设置信度失真预算为ε,这表示模型提供者能够容忍的置信度失真的上界,即:
我们这里使用l1范数作为距离度量,即:
防御
有了这些基础之后,我们就可以来定义如何防御成员推理攻击了:
给定防御分类器的决策函数g,置信度失真预算ε,真实置信度分数向量s,防御者的目标是通过解决如下优化问题找到随机噪声添加机制M*:
目标函数是为了实现目标1,而约束条件则是为了实现目标2
第一个约束意味着添加的噪声不会改变查询样本的预测标签;第二个约束是指置信值失真以预算ε为界;最后两个约束意味着噪声置信度向量仍然是概率分布。
我们根据g(s)是否为0.5来假设两个场景
场景1:g(s)=0.5,此时上面的优化问题很容易求解,将概率为1的噪声向量0相加的机制就是最优的随机噪声添加机制,其目标函数值为0。
场景2:g(s)不等于0.5.此时解决优化问题的主要挑战是随机化噪声添加机制是真实置信度向量在连续噪声空间上的概率分布。噪声空间由满足优化问题四个约束条件的噪声向量组成。因此,概率分布的表示和优化问题的求解具有挑战性。为了解决这个问题,取决于防御分类器的决策函数g的输出,噪声空间可以分为两组,这。对于一组噪声向量,如果我们将其中任何一个加到真实置信度得分向量中,则决策函数g输出0.5作为成员成员的概率。对于另一组中的噪声向量,如果我们将它们中的任何一个添加到真实置信度得分向量中,则决策函数g输出的成员数据概率不为0.5。
在此基础上,我们提出了一个两阶段框架来近似求解优化问题。具体来说,在第1阶段,对于每组,我们找到具有最小置信度分数失真(即d(s, s + n)最小)的噪声向量作为噪声组的代表性噪声向量。为了减小信噪比失真,我们选取了信噪比失真最小的噪声向量。由于g(s)不等于0.5,所以第二噪声组选取的代表性噪声向量为0。我们用r表示第一噪声组的选定代表性噪声向量。在第二阶段,我们假设随机噪声相加机制是两个代表性噪声向量上的概率分布,而不是整个噪声空间。具体来说,防御者以一定的概率将具有代表性的噪声向量r加入到真实置信度得分向量中,而不使用其余的概率添加任何噪声。
我们具体来看看
阶段1:找到r
我们将找r的过程作为求解优化问题:
我们的目标本质上在找一个噪声向量r,其带给置信度分数向量的效用损失是最小的,同时当输入为噪声置信度分数向量时决策函数g会输出0.5。我们可以通过求解下面的优化问题来找到r
其中s是真实置信度分数向量,目标函数是希望置信度失真最小,第一个约束意味着噪声不会改变预测标签,第二个约束意味着防御分类器的决策函数输出0.5(即,防御分类器的预测是随机猜测),后两个约束意味着噪声置信度向量仍然是一个概率分布。
现在关键来了,求解这个优化问题可以看做是在寻找一个对抗样本来欺骗防御分类器。s是原样本,s+r是对抗样本
解决这个问题的一个简单方法是生成满足效用损失约束的随机噪声向量。特别地,我们可以生成一个随机向量r ‘,它的元素是非负的,并且和为1。例如,我们首先从区间[0,1]中均匀随机抽取一个数字r1 ‘作为第一项。然后,我们从区间[0,1 -r1 ‘]中均匀随机抽取一个数字r2 ‘作为第二项。我们重复这个过程,直到最后一项是1减去前一项的和。然后,我们将r ‘的最大分量交换到位置j以满足第一个约束条件。最后,我们将r = r ‘−s作为噪声向量,它是上式优化问题的一个解。不过由于噪声向量不是最优的,而且很难满足sj +rj ≥ 0的约束条件,这种随机方法实现了次优的隐私-效用权衡。
所以我们尝试通过通过变量的改变和在目标函数中加入约束来解决这个优化问题。
首先通过变量的变化来消除对概率分布的约束,因为我们认为目标分类器的输出层是softmax,真实置信度分数向量s是一个向量z的softmax函数,向量z是在倒数第二个层神经元的输出,也就说我们常说的logits。在形式上,我们有:
更进一步,我们将噪声置信度向量建模如下:
其中e是一个新的向量变量。对于e的任意值,噪声置信度向量s + r为概率分布,即满足最后两个约束条件。因此,在优化问题中,我们将真实置信度向量s改变为softmax (z),将变量r改变为softmax (z + e)−softmax (z),之后可以得到如下优化问题:
在上面的优化问题中求解出e后,我们可以得到如下的噪声向量
现在还剩下两个约束,他们是高度非线性的,为此,我们将他们加入目标函数中
因为防御分类器的输出层有sigmoid激活函数,因此我们有
分母中的h()那一项是当防御分类器以噪声置信度向量softmax(x+e)为输入时的倒数第二层的神经元的输出。g(softmax (z + e)) = 0.5 也就意味着h(softmax(z + e)) = 0
因此,我们将最后一个约束条件转换成了下面的损失函数:
当h(sof tmax(z + e))接近0时,L1会比较小
接下来要把剩下的最后一个约束转换成目标函数
我们设查询样本的预测标签为l,即:
那么剩下的那个约束就意味着zl + el是向量z + e中的最大项,因此我们有如下不等式约束
进一步将不等式约束转换为如下损失函数:
其中的ReLU函数定义为
如果下式成立
则损失函数L2为0
将每个约束都转换为目标函数后,我们就可以得到下面的无约束优化问题
其中
接下来的问题就是求解上式。我们设计了一种基于梯度下降的求解无约束优化问题的算法。
算法如下
由于我们的目标是找到一个具有小的置信分数失真的噪声向量,我们迭代地搜索一个大的c3。对于每个给定的c3,我们使用梯度下降法求出满足约束条件的e。当我们找不到满足这两个约束条件的向量e时,搜索c3的过程就停止了。在给定c2、c3和学习速率β后,我们迭代更新矢量变量e。
因为我们将约束条件转换为了目标函数方程,这并不能保证他们迭代梯度下降过程中符合要求。因此,在梯度下降的每次迭代中,我们检查这两个约束是否满足(即算法1中的第8行)。具体来说,当预测的标签发生变化或logit h的符号没有变化时,我们继续梯度下降过程。换句话说,当两个约束条件都满足时,我们停止梯度下降过程。我们用
来近似前面的最后一个约束。
阶段2
在第一阶段结束之后,我们有两个有代表性的噪声向量。在第二阶段中,我们假设随机噪声添加机制是两个代表性噪声向量上的概率分布,而不是整个噪声空间。具体地说,我们认为防御者以概率p和1 – p分别选取具有代表性的噪声向量r和0,防御者将选取的代表性噪声向量加到真实置信度分数向量中。通过这样的简化,可以将优化问题简化如下:
上式的约束意味着期望的置信度失真受预算限制。我们可以推导出简化后的优化问题的解析解。解析解如下:
实验分析
作者在文中是使用三类不同的数据集:
Location:每个特征表示用户是否访问了特定的区域或位置类型
Texas100:每个特征代表损伤的外因(如自杀、药物滥用)、诊断、患者所经历的程序和一些通用信息(如性别、年龄和种族)
CH-MNIST:该数据集用于对结直肠癌患者组织学上的不同组织类型进行分类
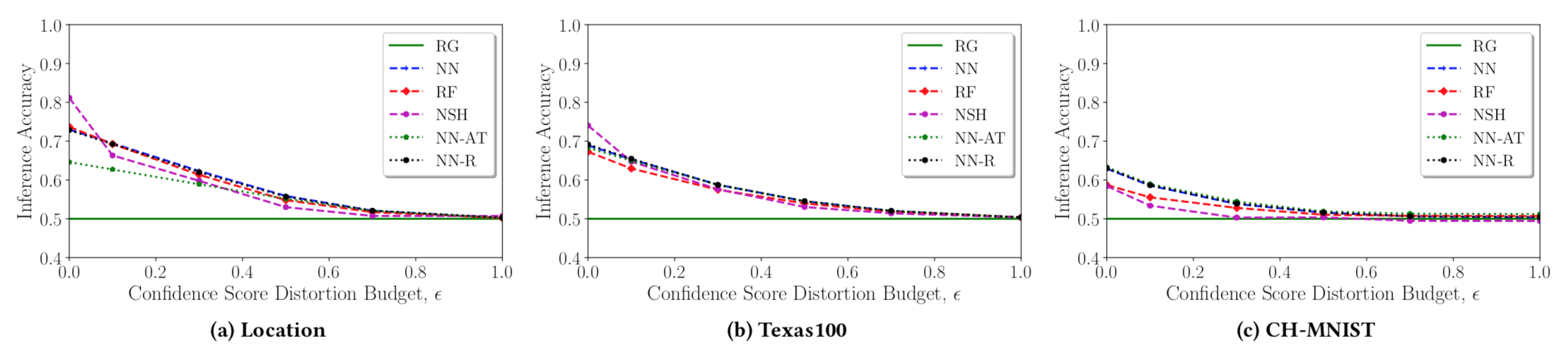
先来看看随着置信度失真预算(即ε)的增加,不同攻击的推断准确性
a,b,c分别对应着不同的数据集,而不同颜色的线代表不同的攻击分类器,我们可以看到,MemGuard可以有效地防御成员推理攻击,由于我们的防御被允许在置信度得分向量中添加更大的噪声,所有攻击的推理准确性都会下降。例如,在Location中,当我们的防御被允许添加预算l1 -范数在0.8左右的噪音时,我们的防御可以将所有评估攻击降低为随机猜测(RG)攻击,都处于0.5的水平;在CH-MNIST上,我们的防御可以将NSH攻击(或其余攻击)减少到随机猜测,当允许添加预期L1-norm在0.3左右的噪声时
然后设计实验来评估成员数据与非成员数据的置信分数向量的不可区分性,给定一个置信度向量s,计算其归一化熵:
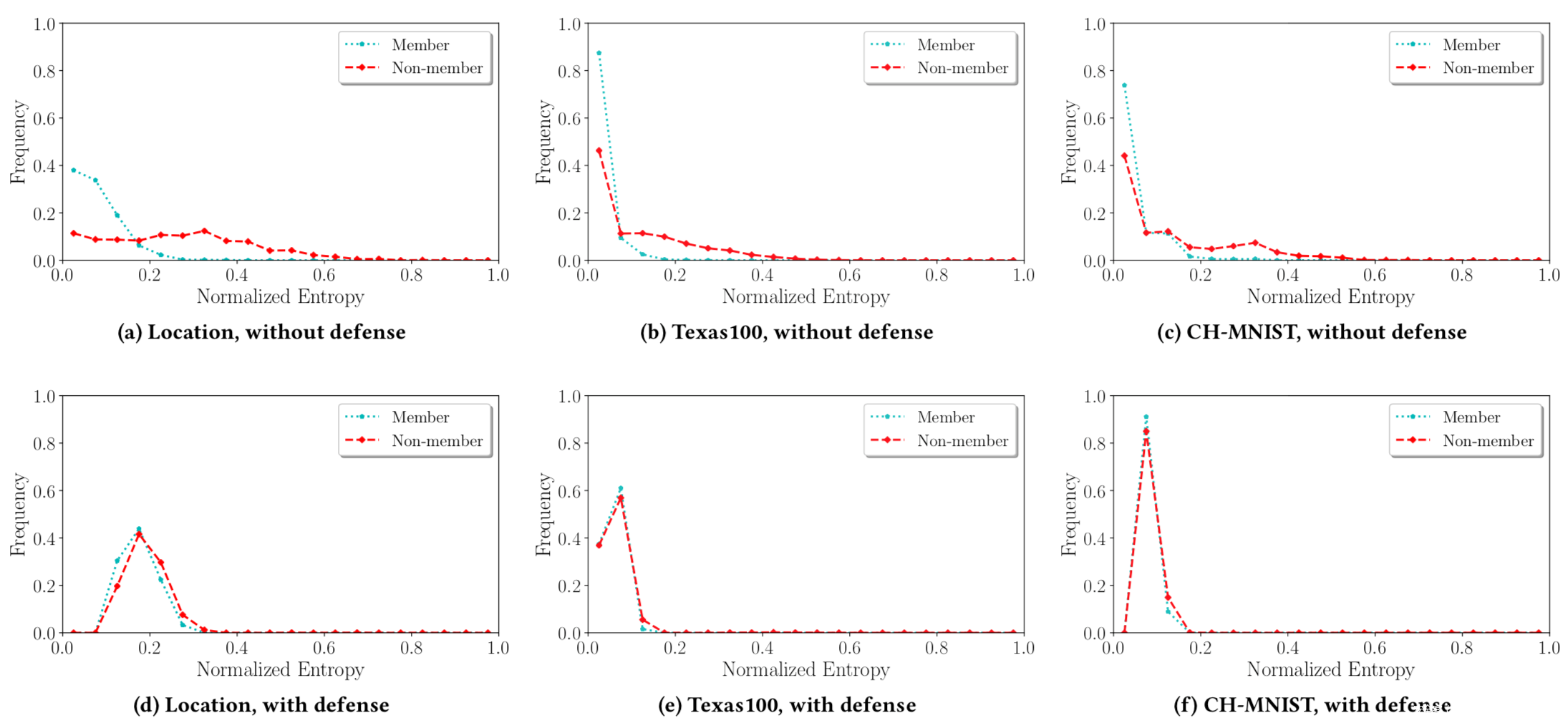
根据这个指标进行测量,结果如下
上面一行是没有防御的,下面是有防御的。图中两条曲线之间的距离对应目标分类器训练数据集的信息泄漏,从图中可以看到,MemGuard大大减少了这种差距。
实战
训练目标分类器
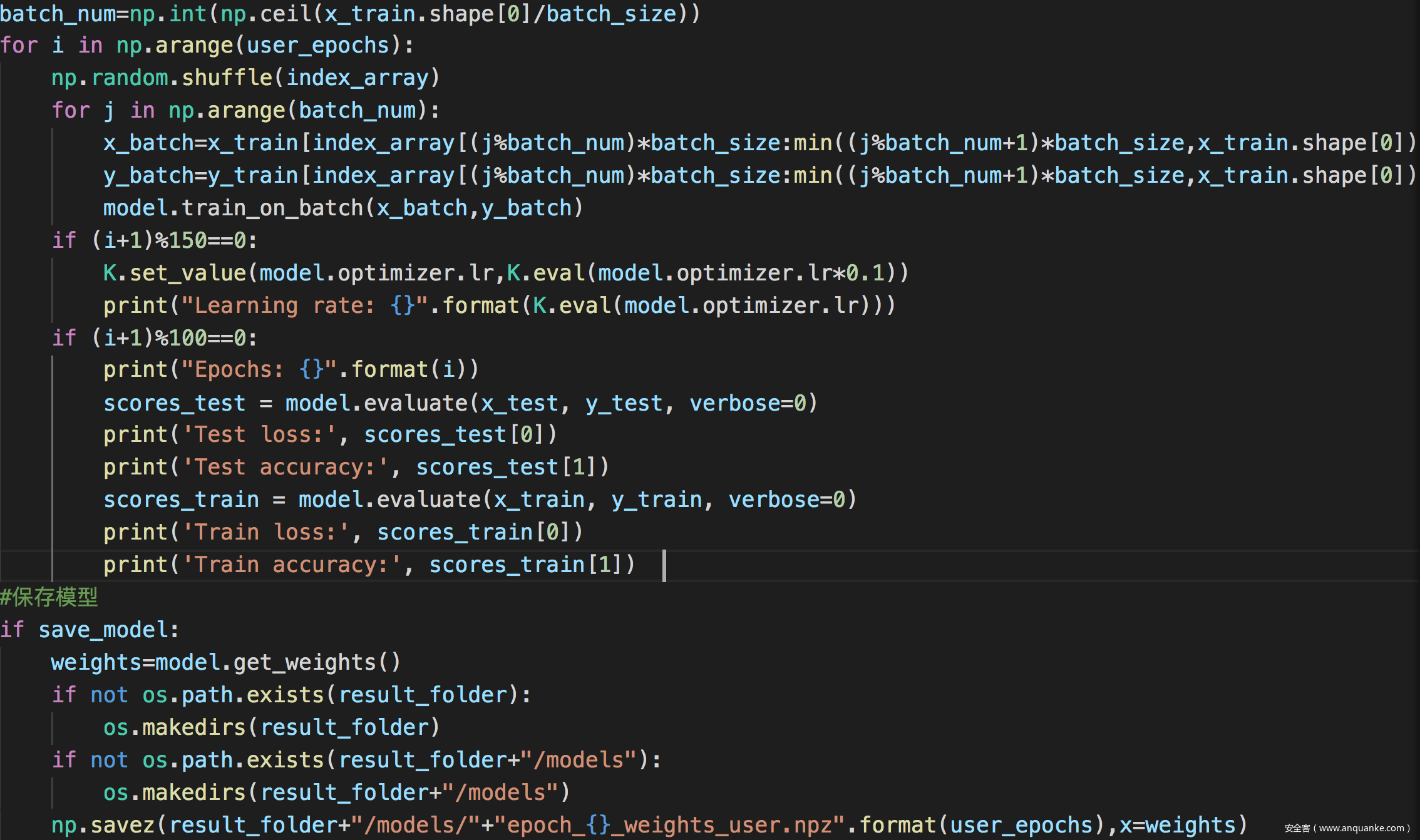
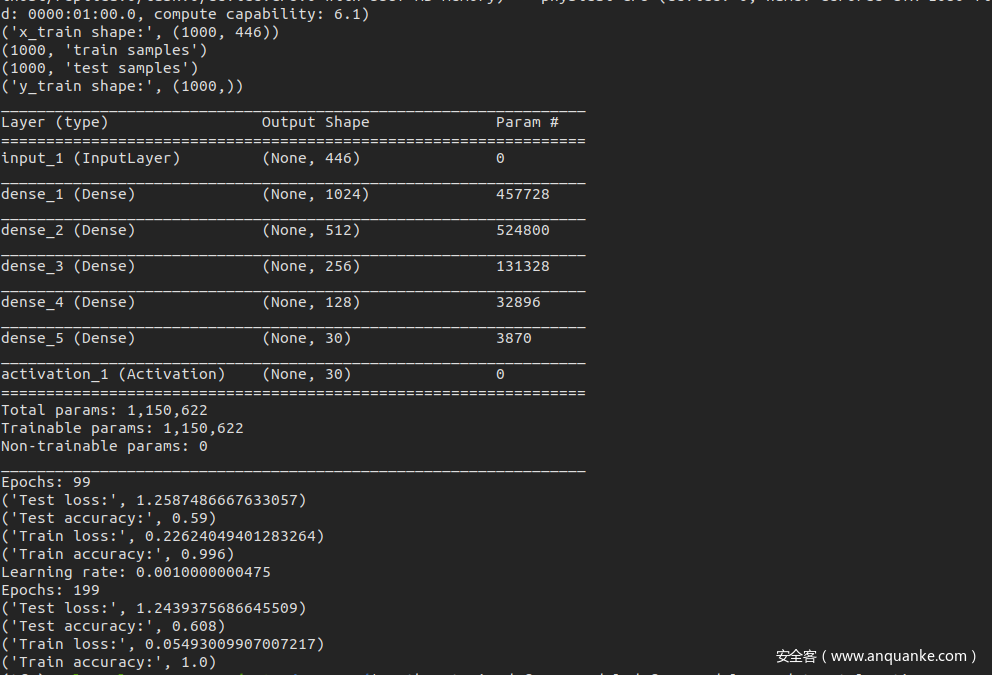
我们使用location数据集,首先训练一个目标分类器
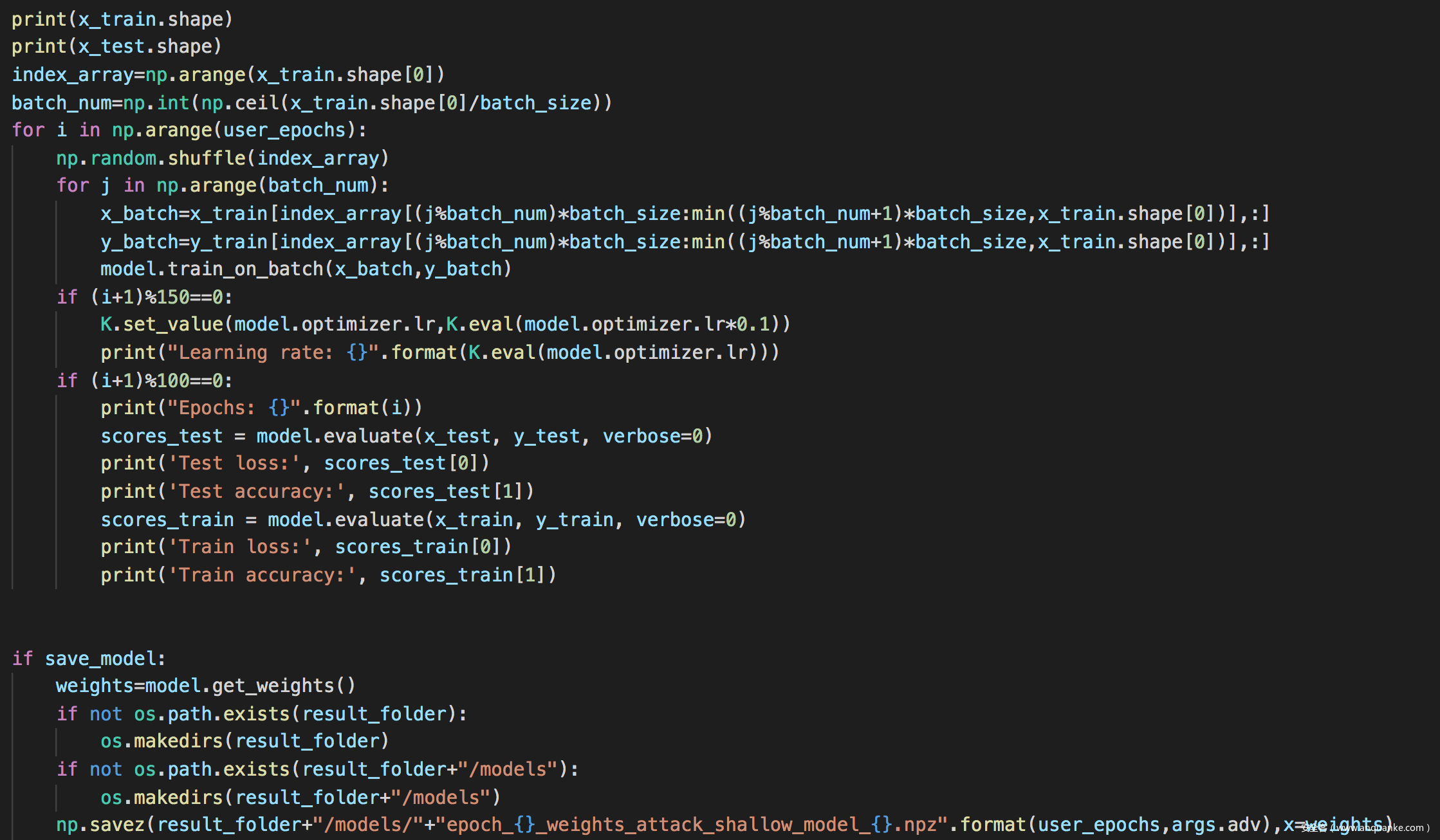
训练过程如下
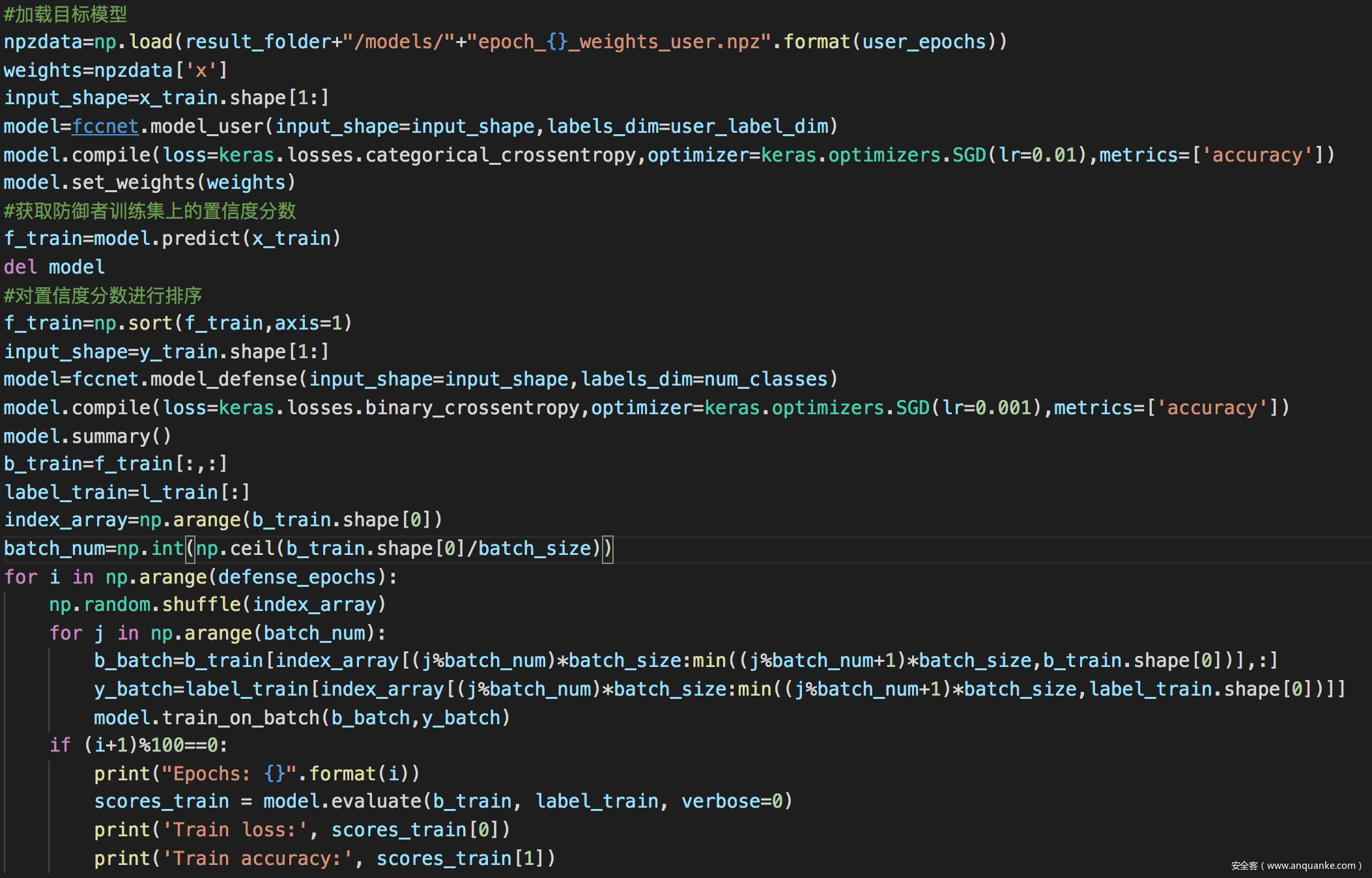
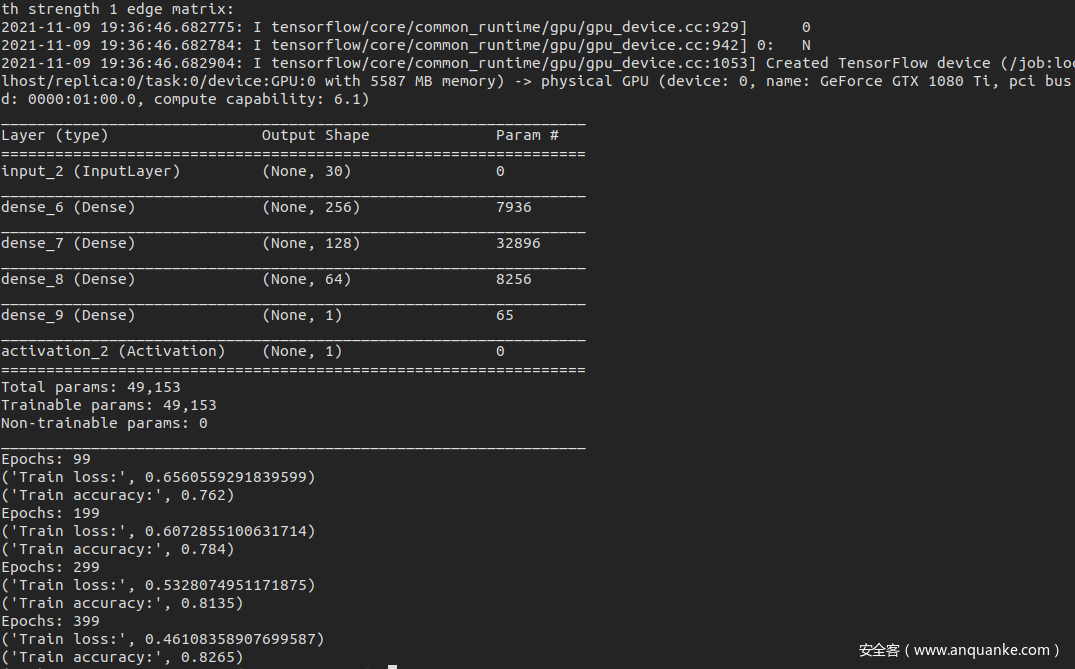
训练防御分类器
训练过程如下
然后是防御框架的训练部分
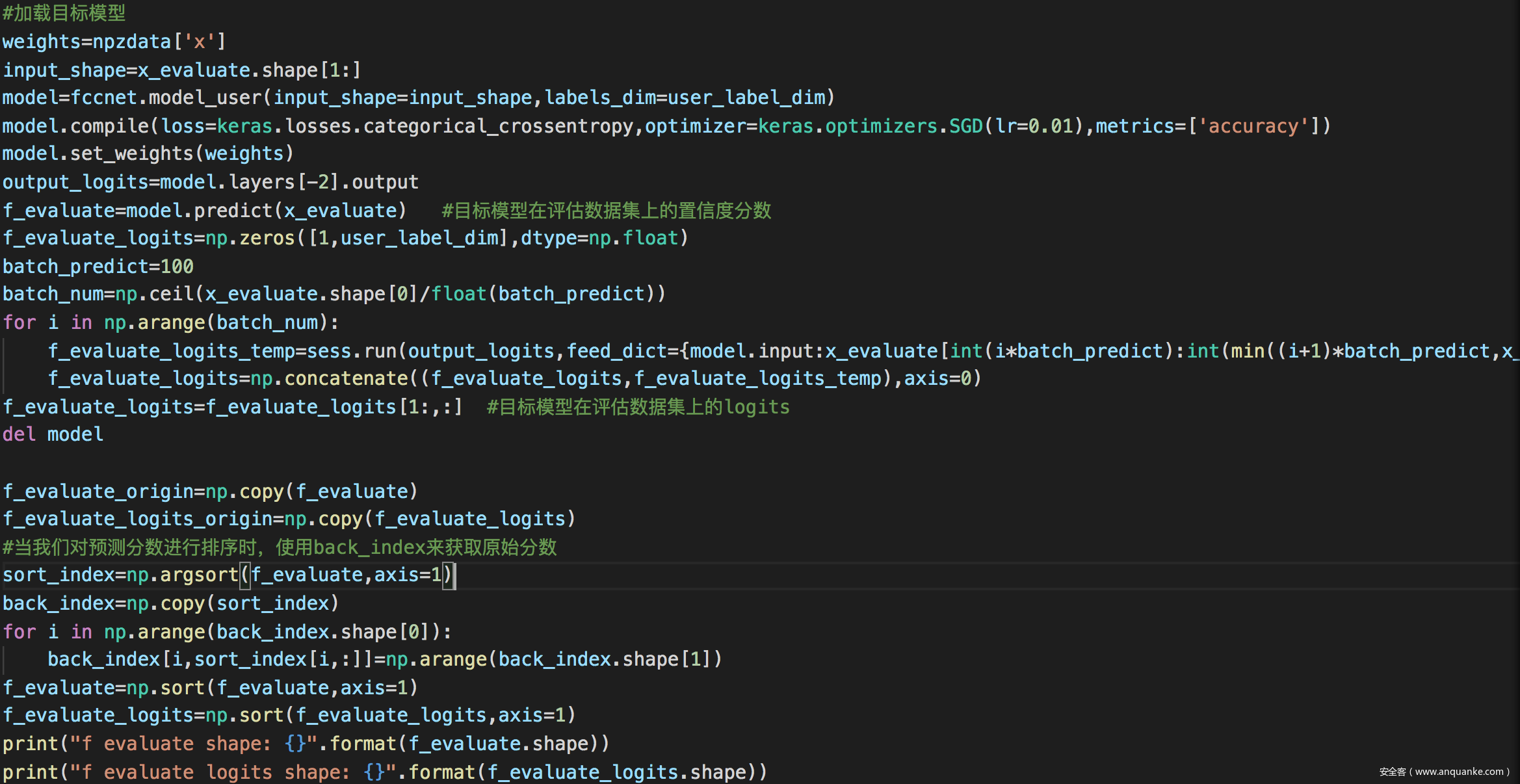
加载目标模型并后去所需置信度分数等信息
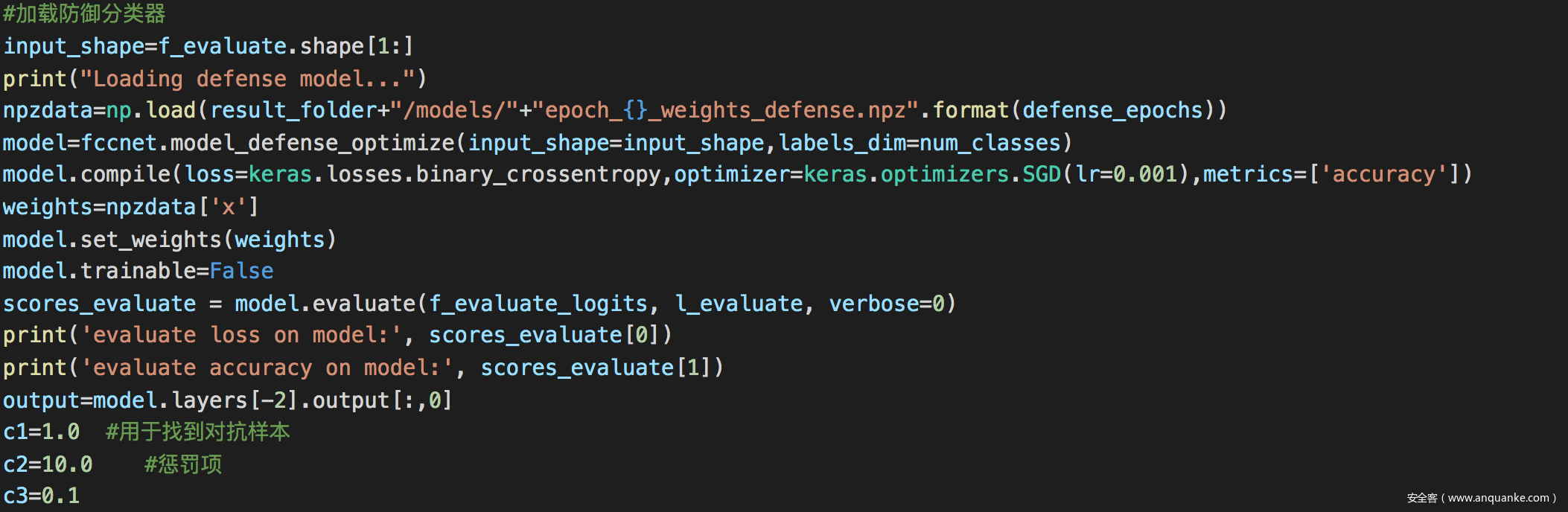
加载防御分类器并设置c1,c2,c3
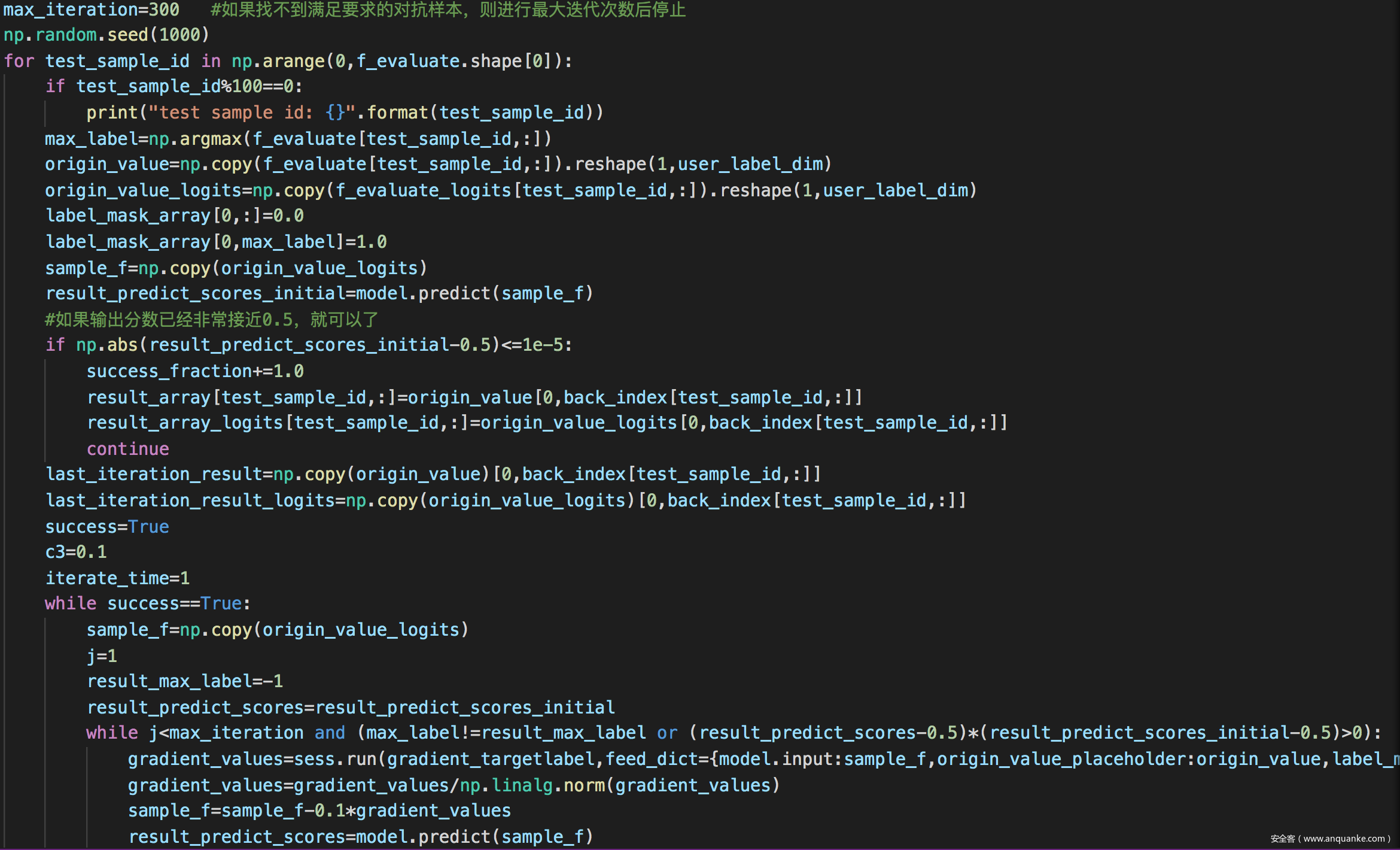
寻找满足优化问题且符合约束条件的噪声向量
求解过程如下
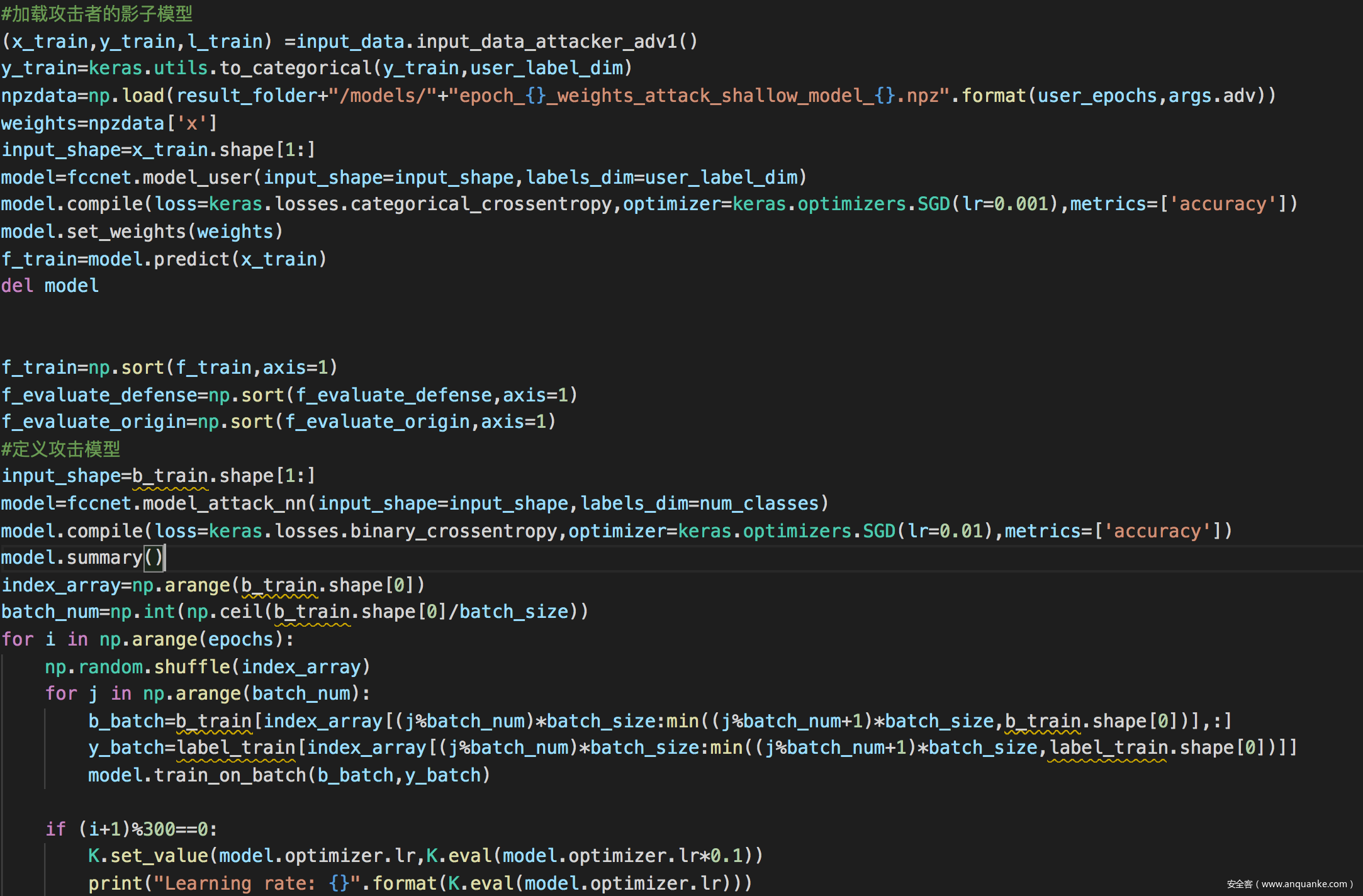
训练攻击所需的影子模型
评估防御效果
攻击者所用的模型
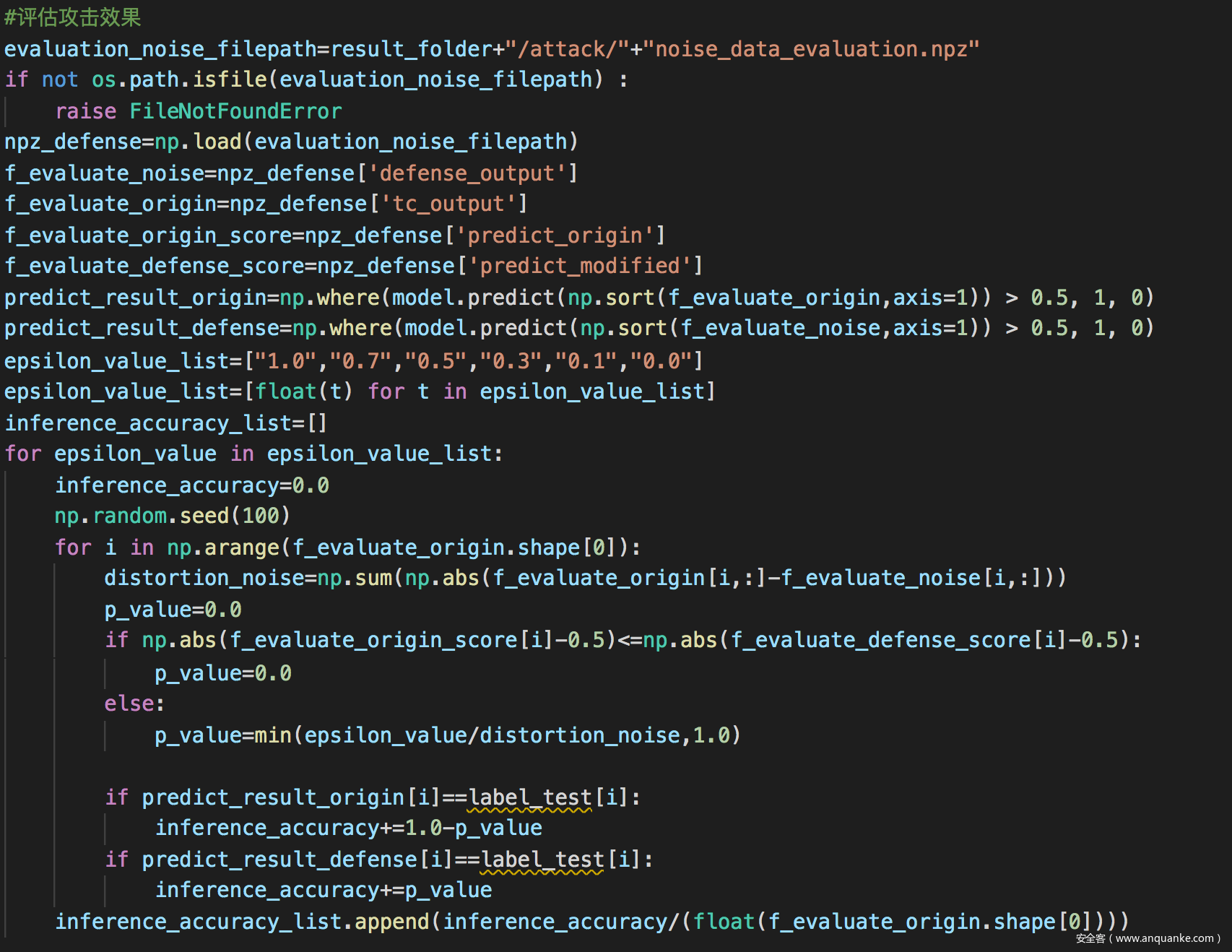
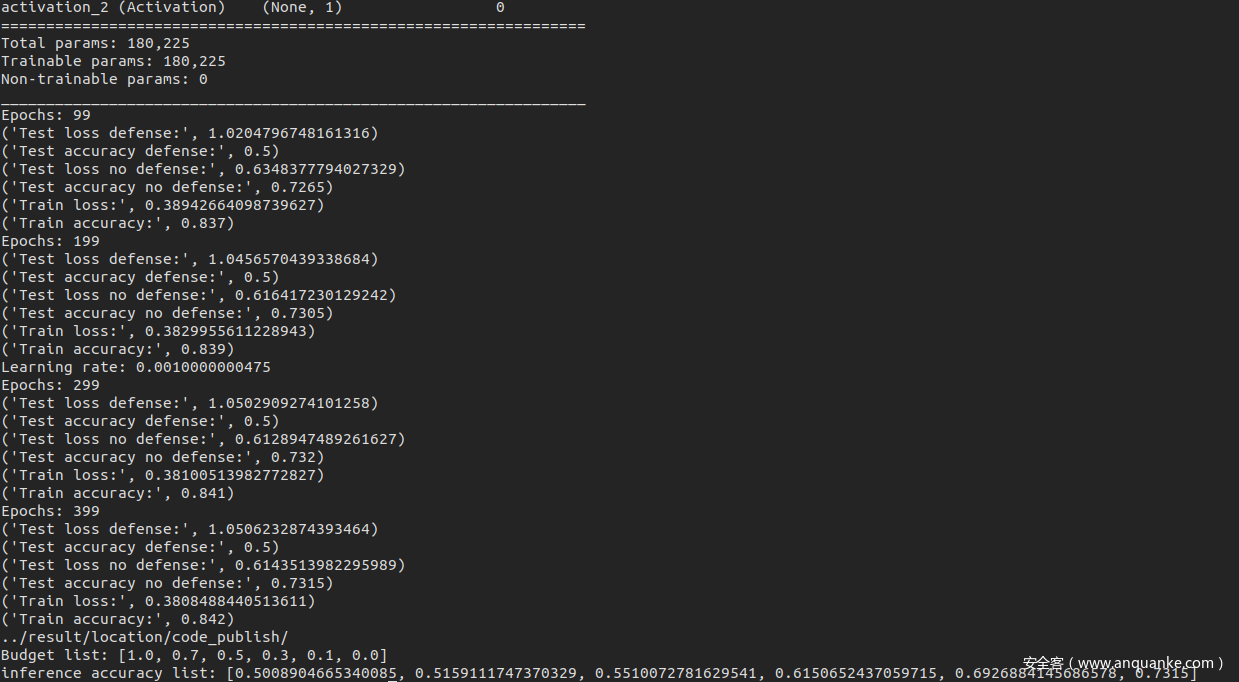
评估攻击效果
从结果可以看到,在应用了MemGuard进行防御之后,成员推理攻击的效果下降到了50%
参考
1.Jia J, Salem A, Backes M, et al. Memguard: Defending against black-box membership inference attacks via adversarial examples[C]//Proceedings of the 2019 ACM SIGSAC conference on computer and communications security. 2019: 259-274.
2.Shokri R, Stronati M, Song C, et al. Membership inference attacks against machine learning models[C]//2017 IEEE Symposium on Security and Privacy (SP). IEEE, 2017: 3-18.
3.Truex S, Liu L, Gursoy M E, et al. Towards demystifying membership inference attacks[J]. arXiv preprint arXiv:1807.09173, 2018.


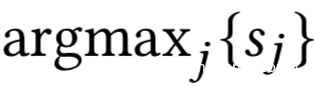
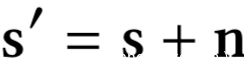

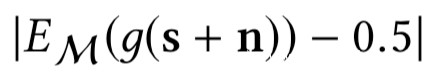
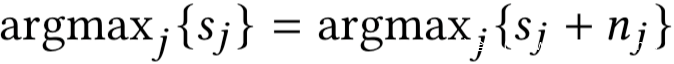


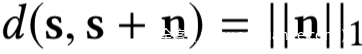
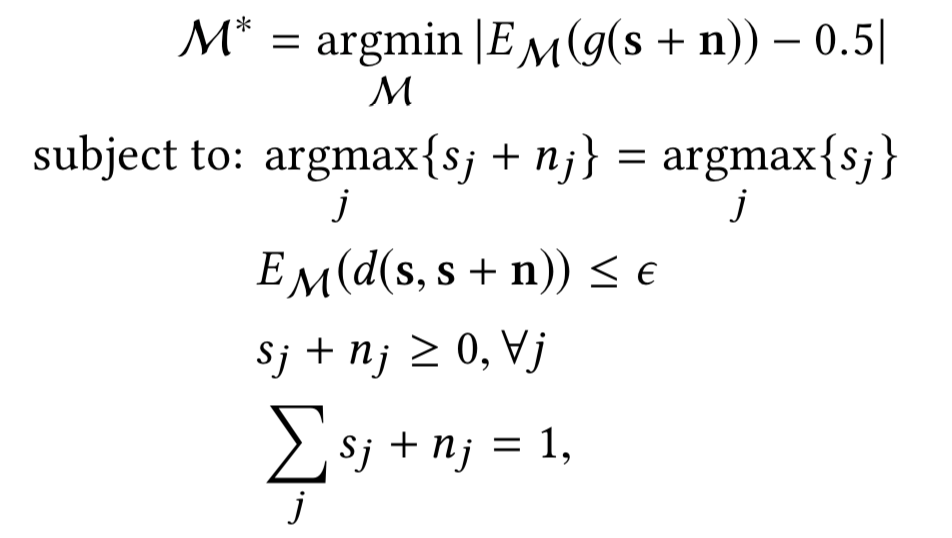




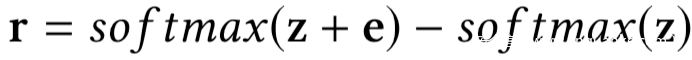

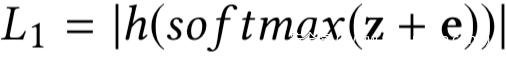
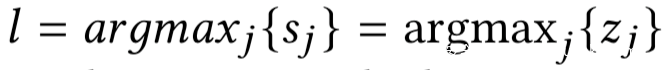
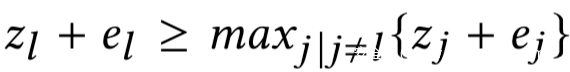
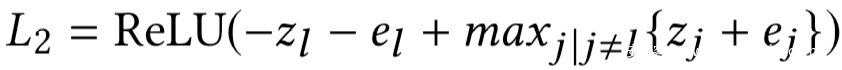
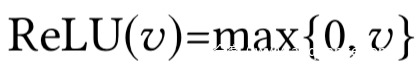
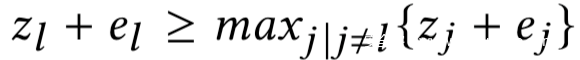
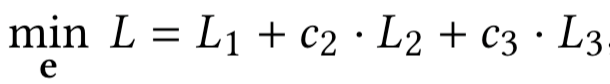
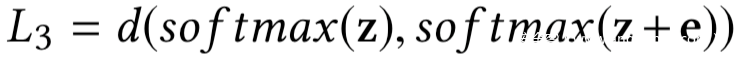


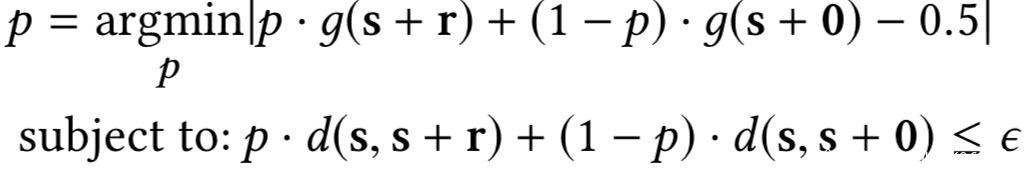

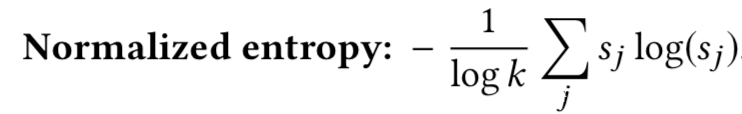









发表评论
您还未登录,请先登录。
登录