最近打了ByteCTF和X-NUCA两场比赛,题目质量很高,(Web手们都哭了)两场比赛自己也分别只做出两道密码学方向的题目,菜狗落泪。
这里记录下自己解题的一个过程,可能废话比较多,当然也是希望能够表达的清楚。如果只是想看最终解题方法的读者可以直接跳解题流程。
ByteCTF
noise
需要前置知识或了解:中国剩余定理
task.py
#!/usr/bin/env python3
from os import urandom
from random import choices
from hashlib import sha256
import signal
import string
import sys
def getrandbits(bit):
return int.from_bytes(urandom(bit >> 3), "big")
def proof_of_work() -> bool:
alphabet = string.ascii_letters + string.digits
nonce = "".join(choices(alphabet, k=8))
print(f'SHA256("{nonce}" + ?) starts with "00000"')
suffix = input().strip()
message = (nonce + suffix).encode("Latin-1")
return sha256(message).digest().hex().startswith("00000")
def main():
signal.alarm(60)
if not proof_of_work():
return
secret = getrandbits(1024)
print("Listen...The secret iz...M2@9c0f*#aF()I!($Ud3;J..."
"Hello?...really noisy here again...God bless you get it...")
for i in range(64):
try:
op = input().strip()
num = input().strip()
except EOFError:
return
if not str.isnumeric(num):
print("INVALID NUMBER")
continue
num = int(num)
if op == 'god':
print(num * getrandbits(992) % secret)
elif op == 'bless':
if num == secret:
try:
from datetime import datetime
from flag import FLAG
except Exception as e:
FLAG = "but something is error. Please contact the admin."
print("CONGRATULATIONS %s"%FLAG)
return
print("WRONG SECRET")
main()
还好,第一题代码量不大,不错不错。看一看,这一题功能很简单,你输入一个数字,他返回给你一个,你的数字 乘上一个992bit的 随机数字 模上一个1024bit的secret 的结果。当然,每次连接上后生成的secret是随机的,但是连上一次,可以交互64次,此时secret是保持不变的。算上你需要一次交互来获取flag,那么就是需要在63次之内“猜”到这个随机生成的secret。
好的,上式子,我们知道中国剩余定理是这样子的
注意这里的模是n,他们彼此互素,然后利用中国剩余定理就可以恢复m(如果m的bit位数小于所有n的bit位数之和的话)
此时,如果k都等于1,那么,
此时n和c就好像等价了,并不能知道模数到底是哪个,换一个说法就是,n和c都可以看作是模数
我们再回到这道题本身,设我们发送的值是n1,n2,n3,secret为s,返回的值是c1,c2,c3
那么就会有这么些式子
这不就是中国剩余定理形式么?所以当等于1,我们就可以利用中国剩余定理来恢复这个secret
需要满足的条件就是,n * randnum = c+s,还有就是n的bit位数之和要大于s的bit位数即1024
当然,这就需要运气了,因为他远程生成的乘数是随机的992bit数字(当然是有可能会小于992bit的),而s是1024bit的数字,所以我们要发送的n大概就是32bit的素数,32*32=1024,所以在63次交互内我们需要服务器生成32个随机数是“好”的,所谓”好””就是要让这个k正好等于1。
我们也可以先本地简单的测一测,可以选择比较小的数给他乘,这样子的k大概率会是0或者1,而0比较好判断,直接判断返回的值是否被我们发送过去的数整除就可以了。而是否正好等于1我们是无法判断的,但凡一组数据插入了一个让k不等于1或者0的数,那么整组数据就作废了。所以我们发送尽量小的数n,让k值大概率只落在0或者1上。
测试代码:
from random import *
primes = [4294966427, 4294966441, 4294966447, 4294966477, 4294966553, 4294966583, 4294966591, 4294966619, 4294966639, 4294966651, 4294966657, 4294966661, 4294966667, 4294966769, 4294966813, 4294966829, 4294966877, 4294966909, 4294966927, 4294966943, 4294966981, 4294966997, 4294967029, 4294967087, 4294967111, 4294967143, 4294967161, 4294967189, 4294967197, 4294967231, 4294967279, 4294967291]
for _ in range(20):
secret = getrandbits(1024)
for num in primes:
print(num * getrandbits(992) // secret),
print
这里我们选择固定了随机数,然后经过20次的测试,下面是测试结果
可以发现,生成的随机数似乎也具有一定程度的局部性,当k出现7,8这样比较大的数的时候,几乎整组的k都比较大,但大部分情况下,由于我们输入的素数比较小,还是只有0和1的情况偏多,但一般也是0偏多,所以,,看脸了,只要有一半以上的1,我们就成功了。
解题流程:
- 确定63个比较小的素数
- 把这些值发送过去
- 收到的值进行一个判断,是否被自己发过去的数整除,是就扔掉,否则就存起来
- 存起来的数超过32个就可以进行CRT尝试恢复secret
- 发送secret过去验证,要是没拿到flag就回到第2步,如此循环往复,加油吧,看你的脸了!
exp:
from pwn import *
from hashlib import sha256
from tqdm import tqdm
from Crypto.Util.number import *
def GCRT(mi, ai):
assert (isinstance(mi, list) and isinstance(ai, list))
curm, cura = mi[0], ai[0]
for (m, a) in zip(mi[1:], ai[1:]):
d = int(GCD(curm, m))
c = a - cura
assert (c % d == 0)
K = c // d * inverse(curm // d, m // d)
cura += curm * K
curm = curm * m // d
cura %= curm
return cura % curm, curm
def proof_of_work(sh):
sh.recvuntil("SHA256(\"")
nonce = sh.recv(8)
sh.recvuntil('with \"00000\"')
for a in tqdm(range(0x30, 0x7f)):
for b in range(0x30, 0x7f):
for c in range(0x30, 0x7f):
for d in range(0x30, 0x7f):
rest = chr(a) + chr(b) + chr(c) + chr(d)
m = (nonce.decode('latin1') + rest).encode("Latin-1")
if sha256(m).digest().hex().startswith("00000"):
sh.sendline(rest)
sh.recvuntil('again...God bless you get it...')
return
def io(sh, num):
sh.sendline('god')
sh.sendline(str(num))
tmp = sh.recvuntil('\n')
if len(tmp) > 100:
return int(tmp)
else:
return int(sh.recvuntil('\n'))
primes = [4294966427, 4294966441, 4294966447, 4294966477, 4294966553, 4294966583, 4294966591, 4294966619, 4294966639, 4294966651, 4294966657, 4294966661, 4294966667, 4294966769, 4294966813, 4294966829, 4294966877, 4294966909, 4294966927, 4294966943, 4294966981, 4294966997, 4294967029, 4294967087, 4294967111, 4294967143, 4294967161, 4294967189, 4294967197, 4294967231, 4294967279, 4294967291]
for i in range(2**10):
sh = remote("182.92.153.117", 30101)
proof_of_work(sh)
length = 32
c = []
index = 0
for i in range(63):
tmp = io(sh, primes[index])
if tmp%primes[index] !=0: #这个判断是剔除k等于0的情况
c.append(-1 * tmp)
index += 1
if index >= 32: #如果超过32个数的k不等于0,我们就可以拿来用了,但也不确定是否这32个数都为1
break
if index < 32:
continue
secret = GCRT(primes, c)[0]
sh.sendline('bless')
sh.sendline(str(secret))
tmp = sh.recvuntil('\n')
if len(tmp) < 5:
tmp = sh.recvuntil('\n')
if b'WRONG' in tmp:
sh.close()
continue
print(tmp)
sh.interactive()
比赛的时候大概跑了2min叭,运气还是可以的。
threshold
需要前置知识或了解:椭圆曲线相关性质
from gmssl import func, sm2
#from flag import FLAG
flag="Congratulations!"
sm2p256v1_ecc_table = {
'n': 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123',
'p': 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF',
'g': '32c4ae2c1f1981195f9904466a39c9948fe30bbff2660be1715a4589334c74c7' +
'bc3736a2f4f6779c59bdcee36b692153d0a9877cc62a474002df32e52139f0a0',
'a': 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC',
'b': '28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93',
}
n = 'FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123'
G = '32c4ae2c1f1981195f9904466a39c9948fe30bbff2660be1715a4589334c74c7' \
'bc3736a2f4f6779c59bdcee36b692153d0a9877cc62a474002df32e52139f0a0'
def sign(tsm2):
data = func.random_hex(len(n))
k1_str = func.random_hex(len(n))
print(tsm2.send_p1(data, k1_str))
backdoor = input('backdoor:').strip()
result = tsm2.output_p1(k1_str, backdoor)
print(result)
def verify(tsm2):
message = input('msg:').strip().encode().strip(b'\x00')
sign = input('sign:').strip().encode().strip(b'\x00')
check = tsm2.verify(sign, message)
if check is True and message == b'Hello, Welcome to ByteCTF2020!':
print(FLAG)
else:
print(check)
class TSM2(object):
def __init__(self, sk):
ecc_table = sm2p256v1_ecc_table
self.ecc_table = ecc_table
self.n = int(ecc_table['n'], 16)
self.para_len = len(ecc_table['n'])
self.ecc_a3 = (int(ecc_table['a'], base=16) + 3) % int(ecc_table['p'], base=16)
self.sk = int(sk, 16)
self.pk = self._kg(self.sk, ecc_table['g'])
self.sks = int(func.random_hex(self.para_len), 16)
self.pks = pow((self.sk + 1) * self.sks, self.n - 2, self.n) % self.n
def send_p1(self, data, k1_str):
e = int(data, 16)
k1 = int(k1_str, 16)
k1 = k1 % self.n
R1 = self._kg(k1, self.ecc_table['g'])
return '%064x%0128s' % (e, R1)
def output_p1(self, k1_str, r_s2_s3):
r = int(r_s2_s3[0:self.para_len], 16)
s2 = int(r_s2_s3[self.para_len:2 * self.para_len], 16)
s3 = int(r_s2_s3[2 * self.para_len:], 16)
k1 = int(k1_str, 16)
d1 = self.sks、
s = (d1 * k1 * s2 + d1 * s3 - r) % self.n
if s == 0 or s == (self.n - r):
return None
return '%064x%064x' % (r, s)
def verify(self, Sign, data):
r = int(Sign[0:self.para_len], 16)
s = int(Sign[self.para_len:2 * self.para_len], 16)
e = int(data.hex(), 16)
t = (r + s) % self.n
if t == 0:
return 0
P1 = self._kg(s, self.ecc_table['g'])
P2 = self._kg(t, self.pk)、
if P1 == P2:
P1 = '%s%s' % (P1, 1)
P1 = self._double_point(P1)
else:
P1 = '%s%s' % (P1, 1)
P1 = self._add_point(P1, P2)
P1 = self._convert_jacb_to_nor(P1)
x = int(P1[0:self.para_len], 16)
return r == ((e + x) % self.n)
def _kg(self, k, Point):
if (k % self.n) == 0:
return '0' * 128
Point = '%s%s' % (Point, '1')
mask_str = '8'
for i in range(self.para_len - 1):
mask_str += '0'
mask = int(mask_str, 16)
Temp = Point
flag = False
for n in range(self.para_len * 4):
if flag:
Temp = self._double_point(Temp)
if (k & mask) != 0:
if flag:
Temp = self._add_point(Temp, Point)
else:
flag = True
Temp = Point
k = k << 1
return self._convert_jacb_to_nor(Temp)
def _double_point(self, Point):
l = len(Point)
len_2 = 2 * self.para_len
if l < self.para_len * 2:
return None
else:
x1 = int(Point[0:self.para_len], 16)
y1 = int(Point[self.para_len:len_2], 16)
if l == len_2:
z1 = 1
else:
z1 = int(Point[len_2:], 16)
T6 = (z1 * z1) % int(self.ecc_table['p'], base=16)
T2 = (y1 * y1) % int(self.ecc_table['p'], base=16)
T3 = (x1 + T6) % int(self.ecc_table['p'], base=16)
T4 = (x1 - T6) % int(self.ecc_table['p'], base=16)
T1 = (T3 * T4) % int(self.ecc_table['p'], base=16)
T3 = (y1 * z1) % int(self.ecc_table['p'], base=16)
T4 = (T2 * 8) % int(self.ecc_table['p'], base=16)
T5 = (x1 * T4) % int(self.ecc_table['p'], base=16)
T1 = (T1 * 3) % int(self.ecc_table['p'], base=16)
T6 = (T6 * T6) % int(self.ecc_table['p'], base=16)
T6 = (self.ecc_a3 * T6) % int(self.ecc_table['p'], base=16)
T1 = (T1 + T6) % int(self.ecc_table['p'], base=16)
z3 = (T3 + T3) % int(self.ecc_table['p'], base=16)
T3 = (T1 * T1) % int(self.ecc_table['p'], base=16)
T2 = (T2 * T4) % int(self.ecc_table['p'], base=16)
x3 = (T3 - T5) % int(self.ecc_table['p'], base=16)
if (T5 % 2) == 1:
T4 = (T5 + ((T5 + int(self.ecc_table['p'], base=16)) >> 1) - T3) % int(self.ecc_table['p'], base=16)
else:
T4 = (T5 + (T5 >> 1) - T3) % int(self.ecc_table['p'], base=16)
T1 = (T1 * T4) % int(self.ecc_table['p'], base=16)
y3 = (T1 - T2) % int(self.ecc_table['p'], base=16)
form = '%%0%dx' % self.para_len
form = form * 3
return form % (x3, y3, z3)
def _add_point(self, P1, P2):
if P1 == '0' * 128:
return '%s%s' % (P2, '1')
if P2 == '0' * 128:
return '%s%s' % (P1, '1')
len_2 = 2 * self.para_len
l1 = len(P1)
l2 = len(P2)
if (l1 < len_2) or (l2 < len_2):
return None
else:
X1 = int(P1[0:self.para_len], 16)
Y1 = int(P1[self.para_len:len_2], 16)
if l1 == len_2:
Z1 = 1
else:
Z1 = int(P1[len_2:], 16)
x2 = int(P2[0:self.para_len], 16)
y2 = int(P2[self.para_len:len_2], 16)
T1 = (Z1 * Z1) % int(self.ecc_table['p'], base=16)
T2 = (y2 * Z1) % int(self.ecc_table['p'], base=16)
T3 = (x2 * T1) % int(self.ecc_table['p'], base=16)
T1 = (T1 * T2) % int(self.ecc_table['p'], base=16)
T2 = (T3 - X1) % int(self.ecc_table['p'], base=16)
T3 = (T3 + X1) % int(self.ecc_table['p'], base=16)
T4 = (T2 * T2) % int(self.ecc_table['p'], base=16)
T1 = (T1 - Y1) % int(self.ecc_table['p'], base=16)
Z3 = (Z1 * T2) % int(self.ecc_table['p'], base=16)
T2 = (T2 * T4) % int(self.ecc_table['p'], base=16)
T3 = (T3 * T4) % int(self.ecc_table['p'], base=16)
T5 = (T1 * T1) % int(self.ecc_table['p'], base=16)
T4 = (X1 * T4) % int(self.ecc_table['p'], base=16)
X3 = (T5 - T3) % int(self.ecc_table['p'], base=16)
T2 = (Y1 * T2) % int(self.ecc_table['p'], base=16)
T3 = (T4 - X3) % int(self.ecc_table['p'], base=16)
T1 = (T1 * T3) % int(self.ecc_table['p'], base=16)
Y3 = (T1 - T2) % int(self.ecc_table['p'], base=16)
form = '%%0%dx' % self.para_len
form = form * 3
return form % (X3, Y3, Z3)
def _convert_jacb_to_nor(self, Point):
len_2 = 2 * self.para_len
x = int(Point[0:self.para_len], 16)
y = int(Point[self.para_len:len_2], 16)
z = int(Point[len_2:], 16)
z_inv = pow(z, int(self.ecc_table['p'], base=16) - 2, int(self.ecc_table['p'], base=16))
z_invSquar = (z_inv * z_inv) % int(self.ecc_table['p'], base=16)
z_invQube = (z_invSquar * z_inv) % int(self.ecc_table['p'], base=16)
x_new = (x * z_invSquar) % int(self.ecc_table['p'], base=16)
y_new = (y * z_invQube) % int(self.ecc_table['p'], base=16)
z_new = (z * z_inv) % int(self.ecc_table['p'], base=16)
if z_new == 1:
form = '%%0%dx' % self.para_len
form = form * 2
return form % (x_new, y_new)
else:
return None
if __name__ == '__main__':
sk = func.random_hex(len(sm2p256v1_ecc_table['n']))
tsm2 = TSM2(sk)
print('pk:%s' %tsm2.pk)
print('pks:%064x'%tsm2.pks)
for i in range(10):
op = input('op: ').strip()
if op == 'sign':
sign(tsm2)
elif op == 'verify':
verify(tsm2)
else:
print("""sign: sign message
verify: verify message""")
啊,这第二题画风就突变,好长的代码,让人失去欲望。但其实呢,大部分都是对sm2的一个实现,其实不用细究。这里我们就直接先提取关键部分,一步一步来啦。
首先最上面的
def sign(tsm2):
data = func.random_hex(len(n))
k1_str = func.random_hex(len(n))
print(tsm2.send_p1(data, k1_str))
backdoor = input('backdoor:').strip()
result = tsm2.output_p1(k1_str, backdoor)
print(result)
def verify(tsm2):
message = input('msg:').strip().encode().strip(b'\x00')
sign = input('sign:').strip().encode().strip(b'\x00')
check = tsm2.verify(sign, message)
if check is True and message == b'Hello, Welcome to ByteCTF2020!':
print(FLAG)
else:
print(check)
俩功能,一个是注册,一个是验证,获取flag的地方就是这个验证,他要求你对message进行一个签名,而message要求是b’Hello, Welcome to ByteCTF2020!’
好的,那我们看看咋样才能给这个message签上名,去找找签名的验证函数。
def verify(self, Sign, data):
r = int(Sign[0:self.para_len], 16)
s = int(Sign[self.para_len:2 * self.para_len], 16)
e = int(data.hex(), 16)
t = (r + s) % self.n
if t == 0:
return 0
P1 = self._kg(s, self.ecc_table['g'])
P2 = self._kg(t, self.pk)
if P1 == P2:
P1 = '%s%s' % (P1, 1)
P1 = self._double_point(P1)
else:
P1 = '%s%s' % (P1, 1)
P1 = self._add_point(P1, P2)
P1 = self._convert_jacb_to_nor(P1)
x = int(P1[0:self.para_len], 16)
return r == ((e + x) % self.n)
这个验证函数有三个输入:r,s,e,然后这里有一个self._kg ,这个其实就是一个椭圆曲线上的一个乘法,所以P1 = s * g,g是椭圆曲线上的一个基点,P2 = t * pk ,代码前头有对pk的定义 self.pk = self._kg(self.sk, ecc_table['g']),所以就是P2 = ((r+s)%n) * sk * g,接下来的操作不难看出,这里就是两个点相加,这里可以print出来看一下输出,是一个点的坐标的十六进制表示的字符串的拼接,x就是这个点的x坐标。最后是一个判断 r == ((e + x) % self.n)
首先e是固定的 b’Hello, Welcome to ByteCTF2020!’。我们能操作的就是r和s了,x是一个算出来的坐标,为了让这个判断成立,我们就需要构造我们的输入r,为了构造r得提前算出P1的x坐标,而P1=P1+P2 = s * g + ((r + s)%n) * sk * g。乍一看我们好像陷入了死锁。这里头怎么又出现了r?
换个思路想想,虽然这里的P1是后来根据我们的输入算出来的,但其实我们也可以先固定这个P1。最后再精心构造一下输入,让他正好算出来是这个P1,
所以假设我们已经知道最后的点P1了,就当他是2g好了,这样我们就可以算出x了,有了x,那么r也就固定下来了,那我们就就只需要构造s让它算出这个P1点了。
我们知道,虽然椭圆曲线的加法和乘法不同于普通的四则运算,但是一些运算法则还是适用的,比如分配律、交换律这些,所以式子:P1=P1+P2 = s * g + ((r + s)%n) * sk * g 可以做一些变形,我们已经知道P1=2g了,外加这条曲线的阶是n(我承认我有赌的成分),所以有
其中r确定了,n确定了,只剩sk了,而sk其实也就是相当于这条椭圆曲线的私钥
这是我们得回过头来看最初的sign函数了
def sign(tsm2):
data = func.random_hex(len(n))
k1_str = func.random_hex(len(n))
print(tsm2.send_p1(data, k1_str))
backdoor = input('backdoor:').strip()
result = tsm2.output_p1(k1_str, backdoor)
print(result)
不能再明显了,backdoor都写给你了,显然是要利用这里来整到sk,
data和k1_str都是不可控的随机数,
然后print了send_p1函数的输出,
def send_p1(self, data, k1_str):
e = int(data, 16)
k1 = int(k1_str, 16)
k1 = k1 % self.n
R1 = self._kg(k1, self.ecc_table['g'])
return '%064x%0128s' % (e, R1)
给的是data和一个R1,R1是k1 * g,是一个曲线上的点,好像没啥用啊,继续看
拿到我们的输入后,程序把k1_str和我们的输入传给了output_p1并给了输出
def output_p1(self, k1_str, r_s2_s3):
r = int(r_s2_s3[0:self.para_len], 16)
s2 = int(r_s2_s3[self.para_len:2 * self.para_len], 16)
s3 = int(r_s2_s3[2 * self.para_len:], 16)
k1 = int(k1_str, 16)
d1 = self.sks
s = (d1 * k1 * s2 + d1 * s3 - r) % self.n
if s == 0 or s == (self.n - r):
return None
return '%064x%064x' % (r, s)
给的是r和s,只要s不等于0,s+r不等于n,
其中我们的输入应该是96字节的,分为三段,代表r,s2,s3,
k1是就是k1_str的整型,程序之前生成的,d1是self.sks,这在代码里头是self.sks = int(func.random_hex(self.para_len), 16)也是一个随机数,但是它和sk跟pks有点关系:self.pks = pow((self.sk + 1) * self.sks, self.n - 2, self.n) % self.n
之所以扯到pks,因为程序一进去他就把这个值给我们了啊
if __name__ == '__main__':
sk = func.random_hex(len(sm2p256v1_ecc_table['n']))
tsm2 = TSM2(sk)
print('pk:%s' %tsm2.pk)
print('pks:%064x'%tsm2.pks)
根据pks的生成式子,其中除了sk和sks我们都知道,
所以我们应该就是要利用这个pks,sks来恢复这个sk,但是怎么获得这个sks 也即 d1 呢,
s = (d1 * k1 * s2 + d1 * s3 - r) % self.n
让s2=0,s3=1,r=0,这样就能得到 s = d1 % n了
显然d1 < n ,故s = d1,并且 d1 + r != n,故能返回。
那么至此,利用链就全了。
解题流程
所以这道题的整个解题流程:
- 构造backdoor = 191 * ‘0’ + ‘1’ 来获取sks,
- 利用pks来获取sk,
- 随便在曲线上取一个点,计算x,根据e来固定r
- 计算
- 传入r,s,e,获取flag
exp
from gmssl import func, sm2
from Crypto.Util.number import *
from TSM2 import *
sk = func.random_hex(len(sm2p256v1_ecc_table['n']))
tsm2 = TSM2(sk)
from pwn import *
context.log_level = 'debug'
sh=remote("182.92.215.134","30103")
sh.recvuntil("pk:")
pk =int(sh.recvuntil("\n")[:-1],16)
sh.recvuntil("pks:")
pks=int(sh.recvuntil("\n")[:-1],16)
tsm2.pks=pks
sh.recvuntil("op:")
sh.sendline("sign")
sh.recvuntil("backdoor:")
sh.sendline("0"*191+"1")
sks = int(sh.recvuntil("\n")[:-1],16)
tsm2.sks=sks
tmp = inverse(tsm2.pks,tsm2.n)
tsm2.sk=tmp*inverse(tsm2.sks,tsm2.n)%tsm2.n-1
tsm2.pk = tsm2._kg(tsm2.sk, tsm2.ecc_table['g'])
assert int(tsm2.pk,16)==pk
print(tsm2.sk)
sh.recvuntil("op:")
sh.sendline("verify")
e=bytes_to_long(b'Hello, Welcome to ByteCTF2020!')
b = 2
B = tsm2._kg(b, tsm2.ecc_table['g'])
x = int(B[0:tsm2.para_len], 16)
r = ((e + x) % tsm2.n)
#b = s + (s+r)*sk
#b = s*(1+sk) + r*sk
#b - r*sk
n=0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
print(tsm2.sk,)
s = (b - r*tsm2.sk)*inverse(1+tsm2.sk,n)%n
sign = '%064x%064x' % (r, s)
print(sign)
sh.recvuntil("msg:")
sh.sendline("Hello, Welcome to ByteCTF2020!")
sh.recvuntil("sign:")
sh.sendline(sign)
sh.interactive()
X-NUCA
weird
需要前置知识或了解:奇异爱德华曲线
可参考资料:https://learnblockchain.cn/article/1627
#!/usr/bin/env sage
from secret import FLAG
assert FLAG.startswith(b"X-NUCA{") and FLAG.endswith(b"}")
def key_gen(bits):
while True:
p = random_prime(2**bits)
q = random_prime(2**bits)
if p % 4 == 3 and q % 4 == 3:
break
if p < q:
p, q = q, p
N = p * q
while True:
x = getrandbits(bits // 2)
y = getrandbits(bits // 2)
if gcd(x, y) == 1 and (x * y) < (int(sqrt(2 * N)) // 12):
e = randint( int(((p + 1) * (q + 1) * 3 * (p + q) - (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))), int(((p + 1) * (q + 1) * 3 * (p + q) + (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))) )
if gcd(e, (p + 1) * (q + 1)) == 1:
k = inverse_mod(e, (p + 1) * (q + 1))
break
return (N, e, k)
if __name__ == "__main__":
bits = 1024
N, e, _ = key_gen(bits)
pt = (int.from_bytes(FLAG[:32], 'big'), int.from_bytes(FLAG[32:], 'big'))
ct = (0, 1)
d = (((pt[1])**2 - 1) * inverse_mod(((pt[1])**2 + 1) * (pt[0])**2, N)) % N
# 2000 years later...:)
for _ in range(e):
ct = ( int((ct[0] * pt[1] + ct[1] * pt[0]) * inverse_mod(1 + d * ct[0] * pt[0] * ct[1] * pt[1], N) % N), int((ct[1] * pt[1] + d * ct[0] * pt[0]) * inverse_mod(1 - d * ct[0] * pt[0] * ct[1] * pt[1], N) % N) )
f = open("output.txt", "wb")
f.write(str((e, N)).encode() + b'\n')
f.write(str(ct).encode())
f.close()
好的,第一题代码量不多,不错不错(嗯?似曾相识,危。。)首先看看他的功能,加密方式是把flag拆成了左右两份,组成一个数对,然后做了e次的操作,得到一个ct数对。这里的e次操作其实就是一个奇异爱德华曲线的一个乘法操作。(题目名不就是weird么?)所以有了e作为加密的公钥,我们自然就要找私钥d,而私钥d,(我承认我有赌的成分)d=inverse(e,(p+1) * (q+1)),(曾经在一篇paper里看到过一眼,虽然用的并非奇异爱德华曲线)
其中p,q是大数N的一个分解。这里阶的确定不是很严格,但先试试啦。那么要这么试的话就要分解N,那就要看到这个keygen的过程了,这里p,q的生成有一点点小要求,然后就是这个e的生成,为了生成这个e,还特意整了个x,y。最后要求gcd(e, (p+1) * (q+1)),唉,这,感觉我的猜测是对的好叭。到了这里,,这还不像西湖论剑的那一道题嘛Wake me until May ends。这道题相关的paper提到
如果e满足一定的条件,
那么x,y就会在e/N的连分数上,并且通过x和y可以获得T:p+q的一个近似。
那么回到这道题本身,e的取值
e = randint( int(((p + 1) * (q + 1) * 3 * (p + q) - (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))), int(((p + 1) * (q + 1) * 3 * (p + q) + (p - q) * int(N**0.21)) * y / (x * 3 * (p + q))) )
这个时候我们就要用到RSA密码系统中用到过的Factoring with high bits known,
显然这里有430bit的不确定位数是满足这个关系的,于是利用这个算法我们最终能成功的分解出p,q来
然后就能算出这个私钥了。
有了私钥了,这个曲线怎么算呢?
d = (((pt[1])**2 - 1) * inverse_mod(((pt[1])**2 + 1) * (pt[0])**2, N)) % N
# 2000 years later...:)
for _ in range(e):
ct = ( int((ct[0] * pt[1] + ct[1] * pt[0]) * inverse_mod(1 + d * ct[0] * pt[0] * ct[1] * pt[1], N) % N), int((ct[1] * pt[1] + d * ct[0] * pt[0]) * inverse_mod(1 - d * ct[0] * pt[0] * ct[1] * pt[1], N) % N) )
这里有个系数d,首先要计算出这个系数d
这个系数d的计算要利用到题目给的ct,
首先看到扭曲爱德华曲线的定义式
针对这一条曲线的加法公式是
针对这一道题他代码里的那个加法式子,我们会发现,这里相当于是扭曲爱德华曲线的系数a = -d
那么再配上一个坐标(x,y),我们就能计算出系数d了。
其实这里可以做一个思考,这个系数d是有啥用?
我们看到这个源码里这个系数d的生成代码d = (((pt[1])**2 - 1) * inverse_mod(((pt[1])**2 + 1) * (pt[0])**2, N)) % N
这里pt[0],pt[1]是flag明文前后两段的十进制数表示,所以d是由flag明文决定的。
我们再变换上述扭曲爱德华曲线的方程:
可以发现就是这个生成代码的方程式,pt[1]代表y,pt[0]代表x
所以其实这个系数d的作用就是保证flag所代表的点在这条曲线上。
好了,系数d也算出来了,怎么利用私钥来解密呢?
显然不可能直接利用原来里的这个循环去加上这些点,
信安数基中就提到过的重复倍加算法了解一下咯~
解题流程
所以这道题的整个解题流程:
- 利用连分数得到x,y(至于怎么确定x,y. 可以根据得到的x,y的bit位数,或者用x,y计算出来的T的bit位数来判断)
- 利用Factoring with high bits known 分解出p,q
- 计算私钥 prikey = inverse(e , (p+1) * (q+1))
- 计算系数
- 利用重复倍加算法做一个乘法计算 mt = d * ct
exp
e,N=(,)
c = continued_fraction(e/N)
for i in range(len(c)):
y=c.numerator(i)
x=c.denominator(i)
if y == 0:
continue
T = e*x//y-N-1
if 1023<(int(T).bit_length()) < 1026: #根据T的bit位数来确定x,y
print(T)
print(x,int(x).bit_length())
print(y,int(y).bit_length())
break
from gmpy2 import * #Factoring with high bits known
_p = (T+iroot(T^2-4*N,int(2))[0])//2
p = int(_p)
n=N
kbits = 430
PR.<x> = PolynomialRing(Zmod(n))
f = x + p
x0 = f.small_roots(X=2^kbits, beta=0.4)[0]
p = p+x0
print("p: ", p)
assert n % p == 0
q = n/int(p)
print("q: ", q)
x,y=(,)
#-d*x*^2 +y^2 = 1+d*x^2*y^2
d = (1-y^2)*inverse_mod(-x^2*y^2-x^2,N)%N #计算系数d
e_inv = inverse_mod(int(e),int((int(p)+1)*(int(q)+1))) #计算私钥prikey
def add(ct,pt): #重复倍加算法的实现
ct = ( int((ct[0] * pt[1] + ct[1] * pt[0]) * inverse_mod(1 + d * ct[0] * pt[0] * ct[1] * pt[1], N) % N), int((ct[1] * pt[1] + d * ct[0] * pt[0]) * inverse_mod(1 - d * ct[0] * pt[0] * ct[1] * pt[1], N) % N) )
return ct
def mul_by_double_adding(ct,n):
pt = (0, 1)
while n > 0:
if n % 2 == 1:
pt = add(ct, pt)
ct = add(ct, ct)
n = n>>1
return pt
(x,y)=mul_by_double_adding((x,y),e_inv) #获取mt,得到flag
from Crypto.Util.number import long_to_bytes
print(long_to_bytes(x)+long_to_bytes(y))
imposter
Toy_AE.py
import os
from Crypto.Cipher import AES
from Crypto.Util.strxor import strxor
from Crypto.Util.number import long_to_bytes, bytes_to_long
class Toy_AE():
def __init__(self):
self.block_size = 16
self.n_size = self.block_size
self.delta = b'\x00' * self.block_size
self.init_cipher()
def init_cipher(self):
key = os.urandom(16)
self.cipher = AES.new(key = key, mode = AES.MODE_ECB)
def pad(self, m, block_size):
return m if len(m) == block_size else (m + b'\x80' + (b'\x00' * (block_size - 1 - len(m))))
def GF2_mul(self, a, b, n_size):
s = 0
for bit in bin(a)[2:]:
s = s << 1
if bit == '1':
s ^= b
upper = bytes_to_long(long_to_bytes(s)[:-n_size])
lower = bytes_to_long(long_to_bytes(s)[-n_size:])
return upper ^ lower
def encrypt(self, msg):
return self.A_EF(msg)
def decrypt(self, ct, _te):
msg, te = self.A_DF(ct)
return msg if _te == te else None
def A_EF(self, msg):
self.Sigma = b'\x00' * self.n_size
self.L = self.cipher.encrypt(b'ConvenienceFixed')
self.delta = b'DeltaConvenience'
m = len(msg) // self.n_size
m += 1 if (len(msg) % self.n_size) else 0
M_list = [msg[i * self.n_size : (i + 1) * self.n_size] for i in range(m)]
C_list = []
for i in range(0, (m-1)//2):
C1, C2 = self.feistel_enc_2r(M_list[2*i], M_list[2*i +1])
C_list.append(C1)
C_list.append(C2)
self.Sigma = strxor(M_list[2*i +1], self.Sigma)
self.L = long_to_bytes(self.GF2_mul(2, bytes_to_long(self.L), self.n_size))
if m & 1 == 0:
Z = self.cipher.encrypt(strxor(self.L, M_list[-2]))
Cm = strxor(Z[:len(M_list[-1])], M_list[-1])
Cm_1 = strxor(self.cipher.encrypt(strxor(strxor(self.L, self.delta), self.pad(Cm, self.block_size))), M_list[-2])
self.Sigma = strxor(self.Sigma, strxor(Z, self.pad(Cm, self.block_size)))
self.L = strxor(self.L, self.delta)
C_list.append(Cm_1)
C_list.append(Cm)
else:
Cm = strxor(self.cipher.encrypt(self.L)[:len(M_list[-1])], M_list[-1])
self.Sigma = strxor(self.Sigma, self.pad(M_list[-1], self.n_size))
C_list.append(Cm)
if len(M_list[-1]) == self.n_size:
multer = strxor(long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size)), self.delta)
else:
multer = long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
return b''.join(C_list), TE
def A_DF(self, ct):
self.Sigma = b'\x00' * self.n_size
self.L = self.cipher.encrypt(b'ConvenienceFixed')
self.delta = b'DeltaConvenience'
m = len(ct) // self.n_size
m += 1 if (len(ct) % self.n_size) else 0
C_list = [ct[i * self.n_size : (i + 1) * self.n_size] for i in range(m)]
M_list = []
for i in range(0, (m-1) // 2):
M1, M2 = self.feistel_dec_2r(C_list[2*i], C_list[2*i +1])
self.Sigma = strxor(M2 ,self.Sigma)
self.L = long_to_bytes(self.GF2_mul(2, bytes_to_long(self.L), self.n_size))
M_list.append(M1)
M_list.append(M2)
if m & 1 == 0:
Mm_1 = strxor(self.cipher.encrypt(strxor(strxor(self.L, self.delta), self.pad(C_list[-1], self.block_size))), C_list[-2])
Z = self.cipher.encrypt(strxor(self.L, Mm_1))
Mm = strxor(Z[:len(C_list[-1])], C_list[-1])
self.Sigma = strxor(self.Sigma, strxor(Z, self.pad(C_list[-1], self.block_size)))
self.L = strxor(self.L, self.delta)
M_list.append(Mm_1)
M_list.append(Mm)
else:
Mm = strxor(self.cipher.encrypt(self.L)[:len(C_list[-1])], C_list[-1])
self.Sigma = strxor(self.Sigma, self.pad(Mm, self.block_size))
M_list.append(Mm)
if len(C_list[-1]) == self.n_size:
multer = strxor(long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size)), self.delta)
else:
multer = long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
return b''.join(M_list), TE
def feistel_enc_2r(self, M1, M2):
C1 = strxor(self.cipher.encrypt(strxor(M1, self.L)), M2)
C2 = strxor(self.cipher.encrypt(strxor(C1, strxor(self.L, self.delta))), M1)
return C1, C2
def feistel_dec_2r(self, C1, C2):
M1 = strxor(self.cipher.encrypt(strxor(C1, strxor(self.L, self.delta))), C2)
M2 = strxor(self.cipher.encrypt(strxor(M1, self.L)), C1)
return M1, M2
task.py
#!/usr/bin/env python3
import os
import random
import string
from hashlib import sha256
from Toy_AE import Toy_AE
from secret import FLAG
def proof_of_work():
random.seed(os.urandom(8))
proof = b''.join([random.choice(string.ascii_letters + string.digits).encode() for _ in range(20)])
digest = sha256(proof).hexdigest().encode()
print("sha256(XXXX+%s) == %s" % (proof[4:],digest))
print("Give me XXXX:")
x = input().encode()
return False if len(x) != 4 or sha256(x + proof[4:]).hexdigest().encode() != digest else True
def pack(uid, uname, token, cmd, appendix):
r = b''
r += b'Uid=%d\xff' % uid
r += b'UserName=%s\xff' % uname
r += b'T=%s\xff' % token
r += b'Cmd=%s\xff' % cmd
r += appendix
return r
def unpack(r):
data = r.split(b"\xff")
uid, uname, token, cmd, appendix = int(data[0][4:]), data[1][9:], data[2][2:], data[3][4:], data[4]
return (uid, uname, token, cmd, appendix)
def apply_ticket():
uid = int(input("Set up your user id:")[:5])
uname = input("Your username:").encode("ascii")[:16]
if uname == b"Administrator":
print("Sorry, preserved username.")
return
token = sha256(uname).hexdigest()[:max(8, uid % 16)].encode("ascii")
cmd = input("Your command:").encode("ascii")[:16]
if cmd == b"Give_Me_Flag":
print("Not allowed!")
return
appendix = input("Any Appendix?").encode("ascii")[:16]
msg = pack(uid, uname, token, cmd, appendix)
ct, te = ae.encrypt(msg)
print("Your ticket:%s" % ct.hex())
print("With my Auth:%s" % te.hex())
def check_ticket():
ct = bytes.fromhex(input("Ticket:"))
te = bytes.fromhex(input("Auth:"))
msg = ae.decrypt(ct, te)
assert msg
uid, uname, token, cmd, appendix = unpack(msg)
if uname == b"Administrator" and cmd == b"Give_Me_Flag":
print(FLAG)
exit(0)
else:
print("Nothing happend.")
def menu():
print("Menu:")
print("[1] Apply Ticket")
print("[2] Check Ticket")
print("[3] Exit")
op = int(input("Your option:"))
assert op in range(1, 4)
if op == 1:
apply_ticket()
elif op == 2:
check_ticket()
else:
print("Bye!")
exit(0)
if __name__ == "__main__":
ae = Toy_AE()
if not proof_of_work():
exit(-1)
for _ in range(4):
try:
menu()
except:
exit(-1)
可恶,果然是这样吗。。不只代码长,甚至附件都有俩。害,慢慢啃咯。。。先不管这个加密的具体是啥,来看看功能是啥叭。程序有俩功能,提供ticket,和检查ticket,获取flag的点在检查ticket,
def decrypt(self, ct, _te):
msg, te = self.A_DF(ct)
return msg if _te == te else None
msg = ae.decrypt(ct, te)
assert msg
uid, uname, token, cmd, appendix = unpack(msg)
if uname == b"Administrator" and cmd == b"Give_Me_Flag":
print(FLAG)
要求你的这个ticket代表的信息是,用户名是Administrator,要执行的命令是Give_Me_Flag,并且还要提供这个ticket的签名Auth来保证他的合法性。
再来看看这个提供ticket有啥,
def apply_ticket():
uid = int(input("Set up your user id:")[:5])
uname = input("Your username:").encode("ascii")[:16]
if uname == b"Administrator":
print("Sorry, preserved username.")
#return
token = sha256(uname).hexdigest()[:max(8, uid % 16)].encode("ascii")
cmd = input("Your command:").encode("ascii")[:16]
if cmd == b"Give_Me_Flag":
print("Not allowed!")
#return
appendix = input("Any Appendix?").encode("ascii")[:16]
msg = pack(uid, uname, token, cmd, appendix)
他要求你提供,uid,用户名,cmd,和额外的可选择的信息。其中,用户名不能等于Administrator,cmd不能等于Give_Me_Flag。(不然这题直接就没了。)然后他会生成一个你的用户名的sha256的摘要,至于存多少长读进你的message呢,由你的uid来决定。
token = sha256(uname).hexdigest()[:max(8, uid % 16)].encode("ascii")
然后一些限制是,除了uid最大为5位数字之外,其余输入最多只能16个字符,并且每个字符的ascii都得在0-128之间(由decode(‘ascii’)限制)。(不然你要是输入\xff,这题也直接就没了)
所以题目意思很明确,你要伪造密文,并且还要能够构造对应的签名来通过合法性验证。让他解密信息后用户名为Administrator,cmd为Give_Me_Flag。然后由于对输入做的诸多限制,(甚至一次连接只能交互4次,除去一次来获取flag,只能交互三次,下一次连接就生成新的Toy_AE对象,生成新的key了)导致漏洞点大概率不会出现在这个task文件中,,那就要找这个Toy_AE算法的洞了。(啊,好长,不想看)
一点点啃叭,先大致随便看看,然后我们有目的性的先来看看生成Auth的过程。(单独拎出来会清晰些)
self.Sigma = b'\x00' * self.n_size
self.Sigma = strxor(M_list[2*i +1], self.Sigma)
if 组数为偶数:
Z = self.cipher.encrypt(strxor(self.L, M_list[-2]))
Cm = strxor(Z[:len(M_list[-1])], M_list[-1])
self.Sigma = strxor(self.Sigma, strxor(Z, self.pad(Cm, self.block_size)))
else:
self.Sigma = strxor(self.Sigma, self.pad(M_list[-1], self.n_size))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
TE = self.cipher.encrypt(strxor(self.Sigma, multer))
可以看到,如果组数为偶数,就会多生成一个Z,而且生成的密文方式也会比较麻烦,那么我们就先利用那个附加信息来控制组数,尽量避免这个麻烦的东西。
这样子的话Sigma第2块、第4块明文、填充后的第5块明文的异或,然后和multer
if len(M_list[-1]) == self.n_size:
multer = strxor(long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size)), self.delta)
else:
multer = long_to_bytes(self.GF2_mul(3, bytes_to_long(self.L), self.n_size))
(multer和L有关,不可知,那就不管了)异或,最后AES加密,返回密文。
由于AES的key也不可知,所以我们想要拿到Auth,没别的方法了。只能在传明文获取Auth时,让我们的msg的第二块和第四块和第五块和真正的能拿到FLAG的msg的明文保持一致了。
这里一个做法就是,本地跑这个程序,把那些麻烦的PoW啥的去去掉,一些限制(比如用户名不能是Administrator)也去去掉,然后打印一些方便我们审计的信息,(当然,熟用那种自带debug编译器的大佬可以忽略,IDLE选手还是比较喜欢print debug大法)
那就是怎么伪造密文了。
先看看密文的生成
C1, C2 = self.feistel_enc_2r(M_list[2*i], M_list[2*i +1])
def feistel_enc_2r(self, M1, M2):
C1 = strxor(self.cipher.encrypt(strxor(M1, self.L)), M2)
C2 = strxor(self.cipher.encrypt(strxor(C1, strxor(self.L, self.delta))), M1)
return C1, C2
我们把明文和密文看成16字节一块,两块一组,两块明文对自己这组生成的密文有影响,但每组明文间的加密是独立的。也就是第一组(第一二块)明文不影响第二组(第三四块)明文生成的第二块密文。
那么,如果我们的uid是1,用户名是Administrator,cmd是Give_Me_Flag,不加信息,
(本地起这个程序,把用户名和cmd的限制给取消掉,然后打印一下M_list)
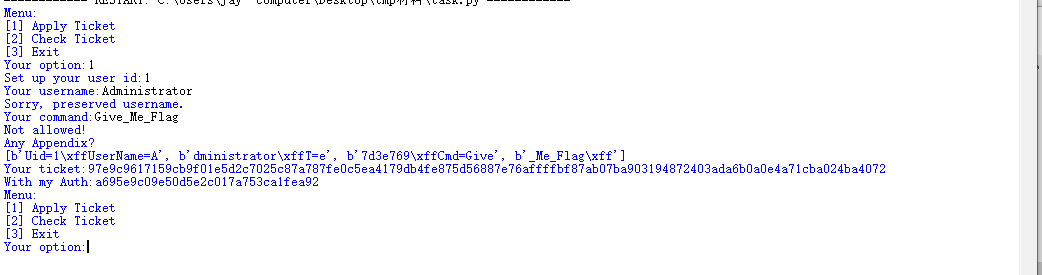
我们会生成4块明文,[b'Uid=1\xffUserName=A', b'dministrator\xffT=e', b'7d3e769\xffCmd=Give', b'_Me_Flag\xff']
前面说了,为了让生成的Auth便于计算,我们要加入附加信息(Appendix)来控制明文组数。
但这里先看看M_list叭,如果我们想要得到Auth,那么我们就得保证我们构造的用户名和cmd在不等于限定值的情况下,M_list的第二组和第四组与用户名为Administrator和cmd为Give_Me_Flag时的M_list的相应分组相同。
这样子看过去,对于我们目前得到的这个M_list是很好构造的,由于Administrator的A在第一组,那么我们注册Bdministrator;由于Give_Me_Flag的Give在第三组,那么我们注册give_Me_Flag就好了。然后加一加Appendix控制下组数。但是注意到第二组最后一位是sha256的首位,而我们要是动了用户名,这个值大概率也有变,所以我们还得控制这个用户名的首位,可能不能是B,我们就在ascii 为0到128之间找一个字符*,让*dministrator的sha256的首位为e就可以了。经过测试,字符‘P’就是一个合适的值
看,上面是目标Auth,下面是我们伪造的用户名和cmd获取的Auth,他们是一致的。所以Auth这一关过了。那就只剩下密文的伪造了。
对于第一组,是由uid和用户名决定的。其中uid不用伪造,问题不大,但是用户名的密文咋办,我们用户名不能等于Administrator,但是又要搞到的Administrator的密文。
这里用到的第一技巧就是,增加uid的长度,反正uid最后模16了,我们控制uid长度为5,用户名为Administratorr(多了一个r),这样子对照一下,
可以发现,多出来的那个r正好被挤到第三组去了,这样子我们的用户名既没有等于Administrator,但是又获得了前两块属于Administrator的msg的密文。
ok。一半的工作完成。
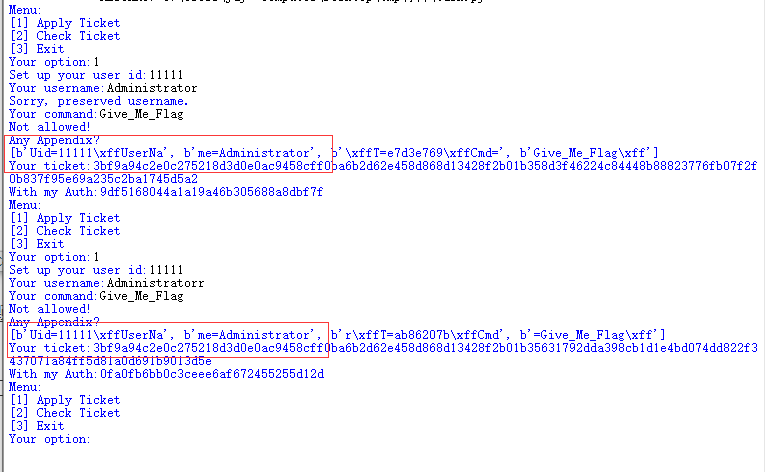
第二组,由于uid那么构造了,那么第二组明文就是这样子的,b'r\xffT=ab86207b\xffCmd', b'=Give_Me_Flag\xff由hash和cmd和组成(这里只是测试,附加信息就先不加了)。
这里我们要的是cmd=Give_Me_Flag的密文,怎么伪造cmd呢?我们不能改变任何一个字符,不然由于AES的存在,密文整个就不一样了。但是输入的cmd又不能等于Give_Me_Flag。这里我们还是用前面的方法,由于这里分组加密的特性,我们把cmd顶到第二块的末尾,大概就是让第二组的第二块明文是这样子,
'Cmd=Give_Me_Flag'
刚好16个字节,然后我们的命令就可以改成Give_Me_Flagg,多的g到第五块去了,咱们就不用管了。至于怎么顶,这里就要利用uid了,在uid长度仍然保持为5的情况下,进行加减,控制hash的长度为12就好了,11111%16 = 7,那就用11116,
可以看到这样\xffT=4110a98d23fc\xff刚好占满了第二组第一块的16字节,'Cmd=Give_Me_Flag占了另一块。而我们输入的cmd命令是Give_Me_Flagg,是能过验证的。这样交互,让他加密,就能得到明文:b'\xffT=4110a98d23fc\xff', b'Cmd=Give_Me_Flag'生成的密文了。但是这里还有个问题,hash由用户名控制,用户名为Administrator的12位hash是e7d3e769f3f5,然而我们又不能注册用户为Administrator,那一个想法就是,碰撞,找一个由可见字符串组成的13位字符串(Administrator的长度),sha256后前12位为e7d3e769f3f5就可以了。然而这显然不现实,12位是96bit,有这算力,比特币不是随便挖?所以这题有解的一个原因就是,这个系统并没有验证用户名的hash,所以你随便整个用户名就好。
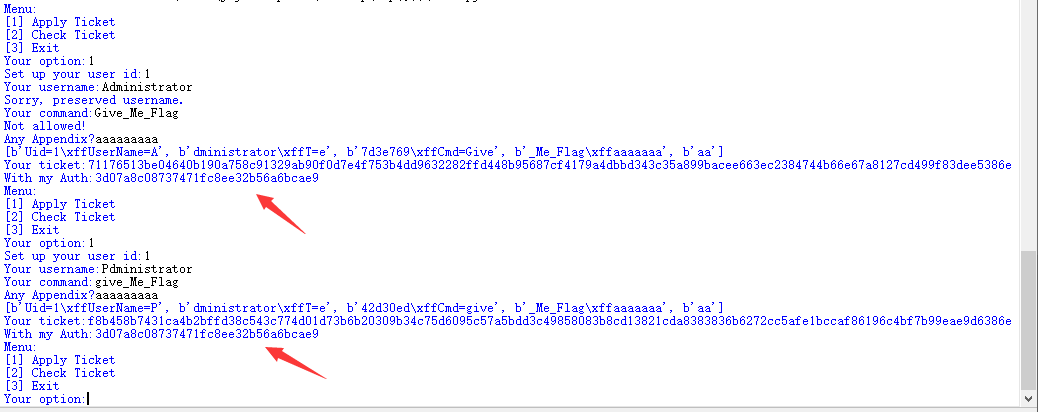
但是新问题产生了,Auth的获取怎么办?现在我们的uid=11116,我们来看看用户名为Administrator,cmd为Give_Me_Flag的情况
想要得到Auth,就得构造同样的第二块、第四块明文,第二块明文还好说,用户名我们多打一个字符就能绕过检查了,而这个字符也会被顶到第三块,对Auth没有影响,并且我们也可以uid相应的减1,让第四块密文不受到影响。但是第四块的明文本身就不好操作啊,这里要是也多打一个字符绕过的话,第五组就多了一个字符,这样产生的Auth就完全对不上了。
所以要把证获取到正确的Auth,我们需要第二块,第四块,第五块分别为:b'me=Administrator', b'Cmd=Give_Me_Flag', b'\xff'
这里我的做法是,缩短uid为两位长,构造用户名为:me=Administrator,控制uid%16为8,构造cmd为Cmd=Give_Me_Flag
可以看到是完全一致的。如果此时打印出来了C_list的话,也会发现,此时这两组产生的C_list的最后一组也是一致的,因为我们这里M_list的到数两组是一致的。
解题流程
所以这道题的整个解题流程:(交互可以直接手撸)
- uid:24,name:me=Administrator,cmd:Cmd=Give_Me_Flag 获取Auth和第三段密文
- uid:11116,name:me=Administratorr,后面随意 获取第一段密文
- uid:11116,name:Administratos,cmd:Give_Me_Flagg 获取第二段密文
- 发送Auth和三段密文的拼接,获取flag
exp
from pwn import *
sh=remote("123.57.4.93","45216")
from pwnlib.util.iters import mbruteforce
from hashlib import sha256
context.log_level = 'debug'
def proof_of_work(sh):
sh.recvuntil("XXXX+b\'")
suffix = sh.recvuntil("\'").decode("utf8")[:-1]
log.success(suffix)
sh.recvuntil("== b\'")
cipher = sh.recvuntil("\'").decode("utf8")[:-1]
print(suffix)
print(cipher)
proof = mbruteforce(lambda x: sha256((x + suffix).encode()).hexdigest() == cipher, string.ascii_letters + string.digits, length=4, method='fixed')
sh.sendlineafter("Give me XXXX:", proof)
proof_of_work(sh)
sh.recvuntil("option:")
sh.sendline('1')
sh.recvuntil("id:")
sh.sendline('24')
sh.recvuntil("name:")
sh.sendline("me=Administrator")
sh.recvuntil("and:")
sh.sendline("Cmd=Give_Me_Flag")
sh.recvuntil("?")
sh.sendline("")
sh.recvuntil("ket:")
ticket=sh.recvuntil("\n")[:-1]
sh.recvuntil("Auth:")
Auth=sh.recvuntil("\n")[:-1]
sh.recvuntil("option:")
sh.sendline("1")
sh.recvuntil("id:")
sh.sendline("65548")
sh.recvuntil("name:")
sh.sendline("Administratorr")
sh.recvuntil("and:")
sh.sendline("Give_Me_Flagg")
sh.recvuntil("?")
sh.sendline("")
sh.recvuntil("ket:")
ticket1=sh.recvuntil("\n")[:-1]
sh.recvuntil("option:")
sh.sendline('1')
sh.recvuntil("id:")
sh.sendline('65548')
sh.recvuntil("name:")
sh.sendline("Administratos")
sh.recvuntil("and:")
sh.sendline("Give_Me_Flagg")
sh.recvuntil("?")
sh.sendline("")
sh.recvuntil("ket:")
ticket2=sh.recvuntil("\n")[:-1]
sh.recvuntil("option:")
sh.sendline('2')
sh.recvuntil("Ticket:")
sh.sendline(ticket1[:64]+ticket2[64:64*2]+ticket[-2:])
sh.recvuntil("Auth:")
sh.sendline(Auth)
sh.interactive()
不得不说这一题出的很精妙,精妙到连输入字符的长度都卡的很死又恰到好处,uid的功能也很灵活,最后的突破点在一个hash未验证。解题花了快一个晚上,除了啃了好久的代码,主要是各种试错。想了很多种构造的方法,包括字节翻转绕过之类的,最后都被一一否决。
但最后构造出来了并拿到flag还是很开心的,虽然再一次认识到了自己和大佬们间的差距。(队伍最后只解出来了两道密码学和一道逆向,差了2名与决赛资格失之交臂,还是挺可惜的)
总结
这两场比赛的四道题目的质量算是比较高叭,byte是两道公钥密码,一个是CRT和脸,一个sm2,。x-nuca是一个奇异爱德华曲线,和一个不知道是不是自创的分组密码。(要是验证hash的话这样的算法系统应该没别的漏洞了,叭?)然后X-NUCA还有一道我没解出来的是LWE,格密码的东西,还是比较生疏。
总的来说这两场比赛,从中确实还是学到了许多东西。也稍微锻炼了下心性(那么长的代码一开始真的让人望而却步,但是一点点啃下来,发现也还好啦。并没有想象中的那么复杂(因为复杂的地方我直接不看,哈哈哈哈))。





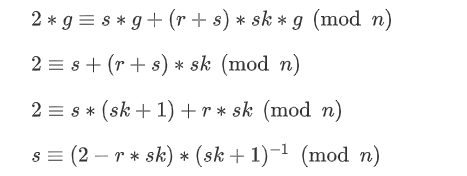
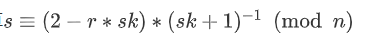







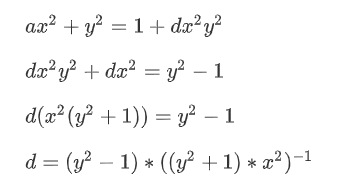









发表评论
您还未登录,请先登录。
登录