前言
密码学学习笔记断更快半年了,最近又重新拾起了对密码学的学习,以一篇对四轮DES的差分分析“复出”。
对于差分密码分析的学习,参考《分组密码的攻击方法与实例分析》
这里就不重新介绍一遍DES的算法流程了,网上一大把。我们研究对DES算法的分析时,由于DES的初始置换及其逆置换均以公开,故在安全性分析时就可以将其忽略。另外我们这里暂且只分析四轮DES,所以有很多概率相关的概念也可以暂时不用涉及。
DES差分分析的关键就在于其S盒差分分布的不均匀特性,何为不均匀特性,即相同的差分进入S盒,输出的差分是不均匀分布的。
不过在详细介绍之前,还是先声明一些概念比较好。
基础概念
迭代分组密码的加密流程
(由于网站对latax语法不太支持,为了读者更好的”视觉体验“,这里我用截图了)
4轮 DES 算法的差分分析
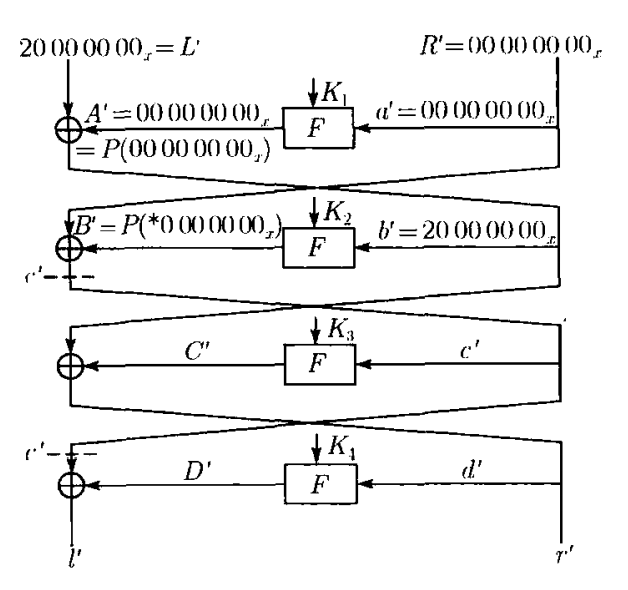
流程图如下
我们记:
- 明文对和相应的差分记为(P,P*) 和 P’
- 密文对和相应的差分记为 (T,T*) 和 T’
- 明文左半部分、右半部分及其差分记为 (L,R) 和 (L’,R’)
- 密文左半部分、右半部分及其差分记为 (l,r) 和 (l’,r’)
- 第1、2、3、4轮函数的输入和输入差分依次记为 a,b,c,d 和 a’, b’,c’,d’
- 第1、2、3、4轮函数的输出和输出差分依次记为 A,B,C,D 和 A’, B’,C’,D’
4轮DES的差分分析本质上仍然是对S和的差分分析,
1.首先我们由密文对 T = (l,r), T* = (l*, r*),可以获得第4轮轮函数的输入对(r,r*),进而也可以获得8个 S 盒的输入对(密钥加之前的数据)为 (E(r),E(r*)); 简单分析 S 盒针对差分的扩散特性以及拓展变换 E 的性质可知,第 4 轮轮函数的输入差分 r’ 也即 d’ 经过拓展变换 E 后(成为 S 盒的输入差分),E(r’) 几乎会让 8 个 S 盒 都活跃,即这个 8 个 S 盒的输入差分都非0。
2.第 4 轮轮函数的输出差分为 D’ = l’ ⊕ c’ = l’ ⊕ a’ ⊕ B’ ,其中 l’ = l ⊕ l*,已知。a’ = 00000000,B’ = P(*0000000),其中 * 为未知的 4 比特向量,表示当第 2 轮轮函数中第一个 S 盒 S_1 的输入差分为 04(由于拓展变换)时可能的输出差分,未知。从而,第4轮轮函数中 8 个 S 盒的输出差分为 P^{-1}(D’)=P^{-1}(l’ ⊕ P(*0000000)) = P^{-1}(l’) ⊕ (*0000000),可求。故第四轮中S2,S3,S4, S5, S6, S7, S8 共 7 个S 盒的输出差分均可求。
3.由上述两个步骤我们可以建立对7个S 盒的差分分析模型,通过对S 盒的差分分析,我们可以恢复 7 × 6 = 42 bit 的轮密钥,由密钥拓展算法,其他 14 bit 的密钥可通过穷尽搜索恢复。
上述攻击中我们未能恢复第 4 轮中进入第一个 S 盒的密钥,是因为它的输出差分未知,因此我们可以选择另外的明文差分,让第二轮的输入差分经过拓展变换后导致第 1 个 S 盒不活跃,即输入差分为0,这样我们就可求得第四轮中第 1 个 S 盒得差分输出了。进而只用再穷尽搜索其他 8bit 密钥。
好的,上面大部分是《分组密码的攻击方法与实例分析》书中的原话。现在,我再用通俗易懂的话来翻译翻译。(也就是讲的再细一点啦)
笔者的“翻译”
我们看到,首先我们构造差分 L’为 20000000 ,R’ 为 00000000,这没什么问题,右下角的x脚标说明这是个十六进制表示,不过注意这里的L’,R’已经是IP 置换过后的了,不是明文差分 X’ 的左右两部分哦,是IP(X’)的左右两部分。
然后我们这些个差分进入第一轮,右边的a’=00000000 进到 F 轮函数,由于是00000000,怎么线性非线性变换都没所谓,先E 盒拓展,再轮密钥加,最后出了S 盒也还是 00000000,再走一个P盒置换P(00000000)也还是 00000000。所以第一轮走完,左边差分等于 A’ ⊕ L’=00000000 ⊕ 20000000=20000000,右边还是原来的 a’=00000000
到了第二轮,这个轮函数的输入是 b’ = A’ ⊕ L’=20000000,先先E 盒拓展,变成40000000,然后分为八组进入S 盒,显然后面 7 组都是0,不会激活 S 盒,那出来还是0。(可能会突然疑惑,轮密钥加呢?看到最上面的差分经过 F 函数各个组件的性质第一条,差分不受轮密钥加的影响,所以后面也都不管它了)但是第一组是以差分为 4 进入 S 盒的,由于性质第三条,S 盒的输出差分不确定,这与输出差分有关,也与具体的输出有关。所以,这一轮 S 盒的输出差分为 *0000000,之后还得 P 盒置换,所以B’ = P(*0000000)。那么第二轮走完,左边等于B’ ⊕ R’ = P(*0000000) ⊕ 00000000=P(*0000000),右边等于b’ = 20000000
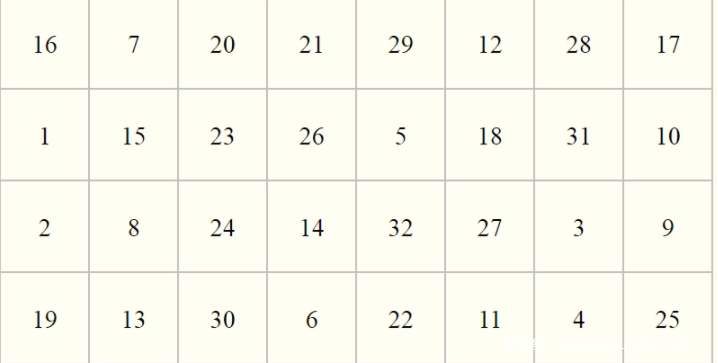
开始第三轮,这一轮开始就要乱起来了。首先这个轮函数的输入是 c’ = B’ ⊕ R’= P(*00000000),我们看一下具体的 P 盒,
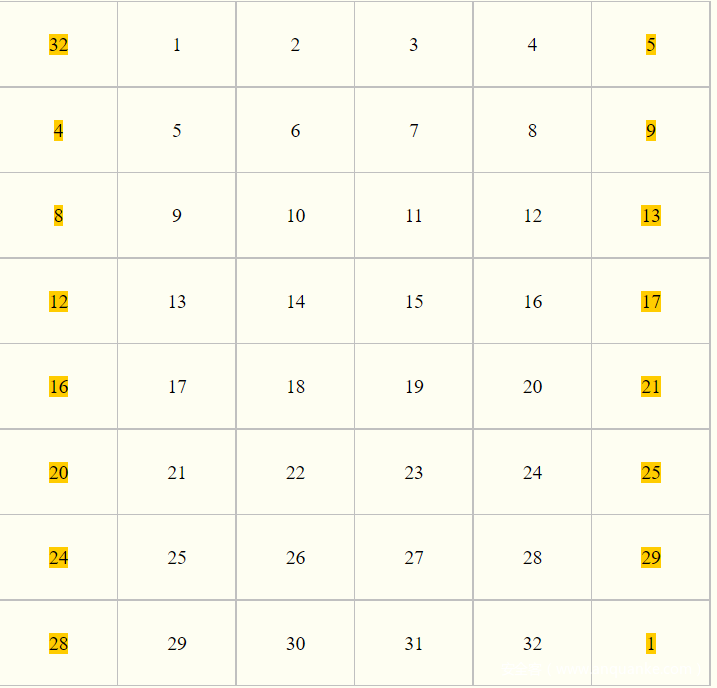
这里我们不确定的前四个bit被扩散到了第3,5,6,8组,也就是说现在我们的c’ = 00*0**0*,然后这里还要先E 盒拓展,看看 E 盒
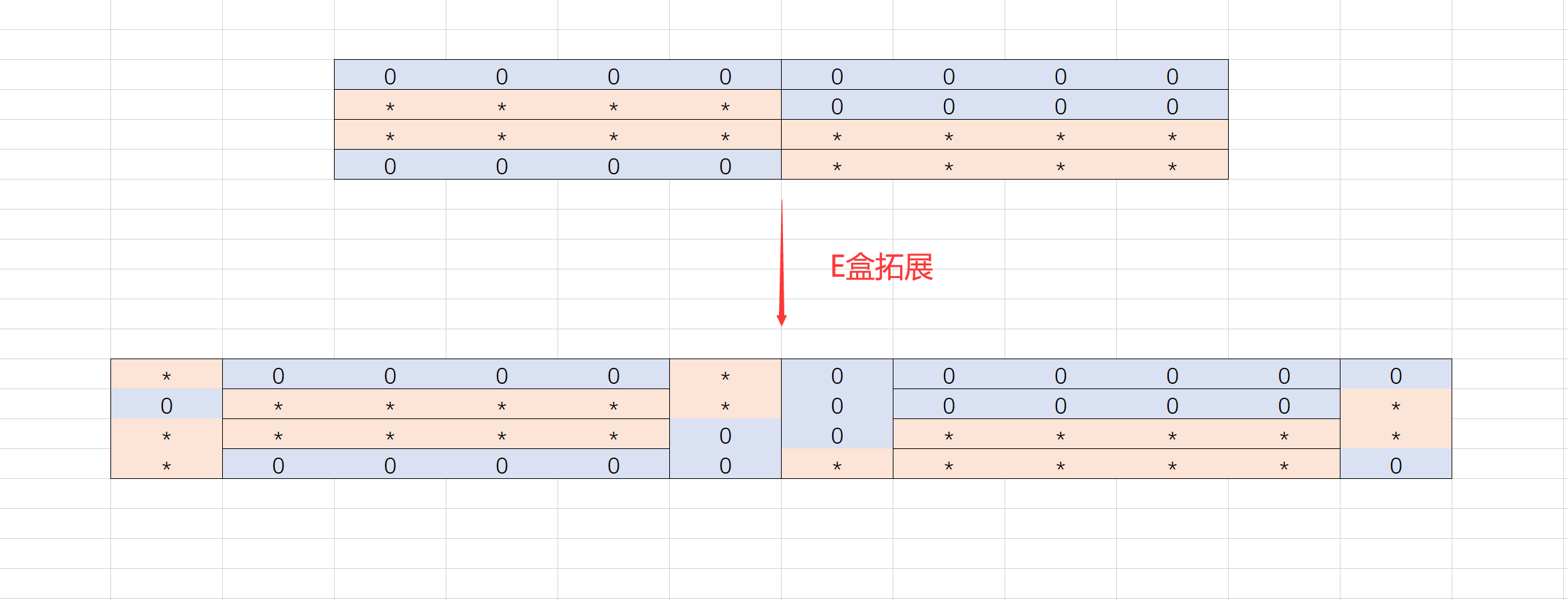
那么进入S 盒前
可以看到,几乎每一组都被”污染了“,只剩第5组还是 0 那么 C’ = ****0***,然后这里还有一个 P 盒置换,那么第三轮走完,左边等于C’ ⊕ b’ = 20000000 ⊕ P(****0***),右边等于c’ = ****0***(注,这里 * 为不确定的意思,进入S 盒前的 * 大概率不等于出 S 盒后的 *)
到最后的第四轮了,此时进入 S 盒的是d’ = C’ ⊕ b’,万幸只有四轮,所以d’ = r’,由于r’ 是可由最后的输出密文右半部分求一个IP 逆置换而来,因此,d’ 已知。
我们直接计算d’ 可以发现 d’几乎不会有 0 bit,也可以推一下,因为 d’ = P(****0***) ⊕ 20000000,而由于这个P 盒置换,第5组最终也会被”污染“,那么可以预见,每一组进入 S 盒的差分都被”污染“了,也就是说每一个 S 盒都会被激活。这也就是书中所说的简单分析 S 盒针对差分的扩散特性以及拓展变换 E 的性质可知,第 4 轮轮函数的输入差分 r’ 也即 d’ 经过拓展变换 E 后(成为 S 盒的输入差分),E(r’) 几乎会让 8 个 S 盒 都活跃,即这个 8 个 S 盒的输入差分都非0。
那么到此四轮DES分析完毕。其实也就说明了一个问题,进入第四轮的 S 盒的输入会激活所有的 S 盒,然后进入第四轮 S 盒的输入差分已知,从第四轮后面7个 S 盒出来的输出差分可求,由此我们可以建立对这7个S 盒的差分分析模型以求出第四轮的轮密钥。
接下来简单讲讲具体怎么求。
首先拿到最后的输出明文差分 Y’,首先对右半边求 IP 逆置换得到 d’=r’,然后对其用 E盒 做拓展置换。先打住,我们去求一下第四轮 S 盒 的输出差分P^{-1}(D’)
我们拿到输出明文差分Y’,对做半边求 IP 逆置换得到 l’ = c’ ⊕ D’,这个c’ = a’ ⊕ B’ = 00000000 ⊕ P(*00000000) ,
第四轮的轮密钥会分为8组,分别和经过 E 盒拓展置换的 8 组输入异或后最终进入 S 盒。这8组输入差分在与轮密钥异或前后是不会变的,但是我们再次强调前面提到过的第三条性质:S 盒:S(x) ⊕ S(x*) = y ⊕ y*,结果不确定,不仅与x ⊕ x* 有关,还与 x 有关。输入的差分没变,但是两次输入的具体值因为轮密钥的异或,会发生变化。因此改变这里的轮密钥,是会使得 S 盒的输出差分受影响的。
但是呢,但是呢,我们不是已经知道输出差分了么?啊哈,那么很显然了,我们只要不断地尝试每个 S 盒那一组的轮密钥——轮密钥加,再 S 盒输出差分,然后对比我们已知的输出差分,如果匹配,则该轮密钥放入待选集合。由于每个 S 盒只用到 6bit 轮密钥,因此穷举复杂度只有 7× 2^6,完全可以接受。然后会出现多解的情况。换一组具有相同差分(非必须,差分为40000000 00000000也可)的明文输入,得到一个新的解集,再取交集即可。根据实际情况,一般取四对差分明文就能有很大概率解出 42 bit的轮密钥。
然后现在有两个选择,一个是选择复杂度为 2^{14} 穷举,另一个是换一下差分,不要激活到第一个 S 盒就行。这样就能恢复全部的48 bit密钥,然后再进行复杂度为 2^8 的穷举,两种复杂度倒也都是能接受的。
有了48bit的轮密钥后,我们知道密钥拓展用的压缩 P 盒
1.所以我们先根据 P 盒将 48 bit 的密钥位置先还原,
2.剩下的空位再直接穷举,最后得到56bit的轮密钥,
3.然后根据轮密钥生成的方式,将第四轮轮密钥还原成最初的密钥,
4.然后我们选取一对服务端生成的明文密文对,用我们的密钥对明文进行加密,
5.观察得到的密文是否与服务端生成的密文一致,若一致则得到正确密钥,否则回到第二步。
至此,4轮DES差分就到此结束了。可以看到,还没有用到概率论的知识,这是因为轮次比较少,前面我们分析的每一轮都是确定的,而等轮次增大到8轮以后就要开始引入统计分析与概率论了,取寻找概率较大的差分路径,这才是差分分析的完全体。
Remark:前面我们提到,DES差分分析的关键就在于其S盒差分分布的不均匀特性,何为不均匀特性,即相同的差分进入S盒,输出的差分是不均匀分布的。现在回头来看看这句话应该就能理解了,如果S盒差分分布均匀,相同地输入差分能够得到相同的输出差分,那么,我们就没办法去穷举验证我们的轮密钥了,因为我们没有了标准去区分密钥的正确与否。
结语
差分分析入门篇到此告一段落,希望接下来能有进阶篇叭,如果我学的会,能够理解的话哈哈哈哈哈哈哈哈哈哈哈哈哈。



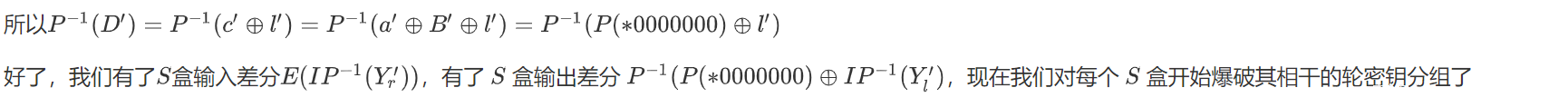







发表评论
您还未登录,请先登录。
登录