前言
我们知道深度学习模型容易受到对抗样本攻击,比如在计算机视觉领域,对图像精心设计的扰动可能会导致模型出错。虽然现在对抗样本的研究非常火,但是模型面临的攻击不止有对抗样本攻击。
Goodfellow(是的,就是GAN之父)团队又设计了一种新的攻击范式,叫做adversarial reprogramming,中文可以叫做对抗重编程。这种攻击范式的目标是对目标模型重新编程,以执行攻击者选定的任务,这种攻击的危害的潜在后果包括窃取MLaaS的计算资源、将人工智能驱动的智能助手当做间谍或垃圾邮件机器人等等,可以重用预训练好的模型来实现攻击者的对抗任务,既然在原理上已经说明这是可行的,那么之后会发展出什么攻击场景、危害行为都是有可能的。
对抗重编程
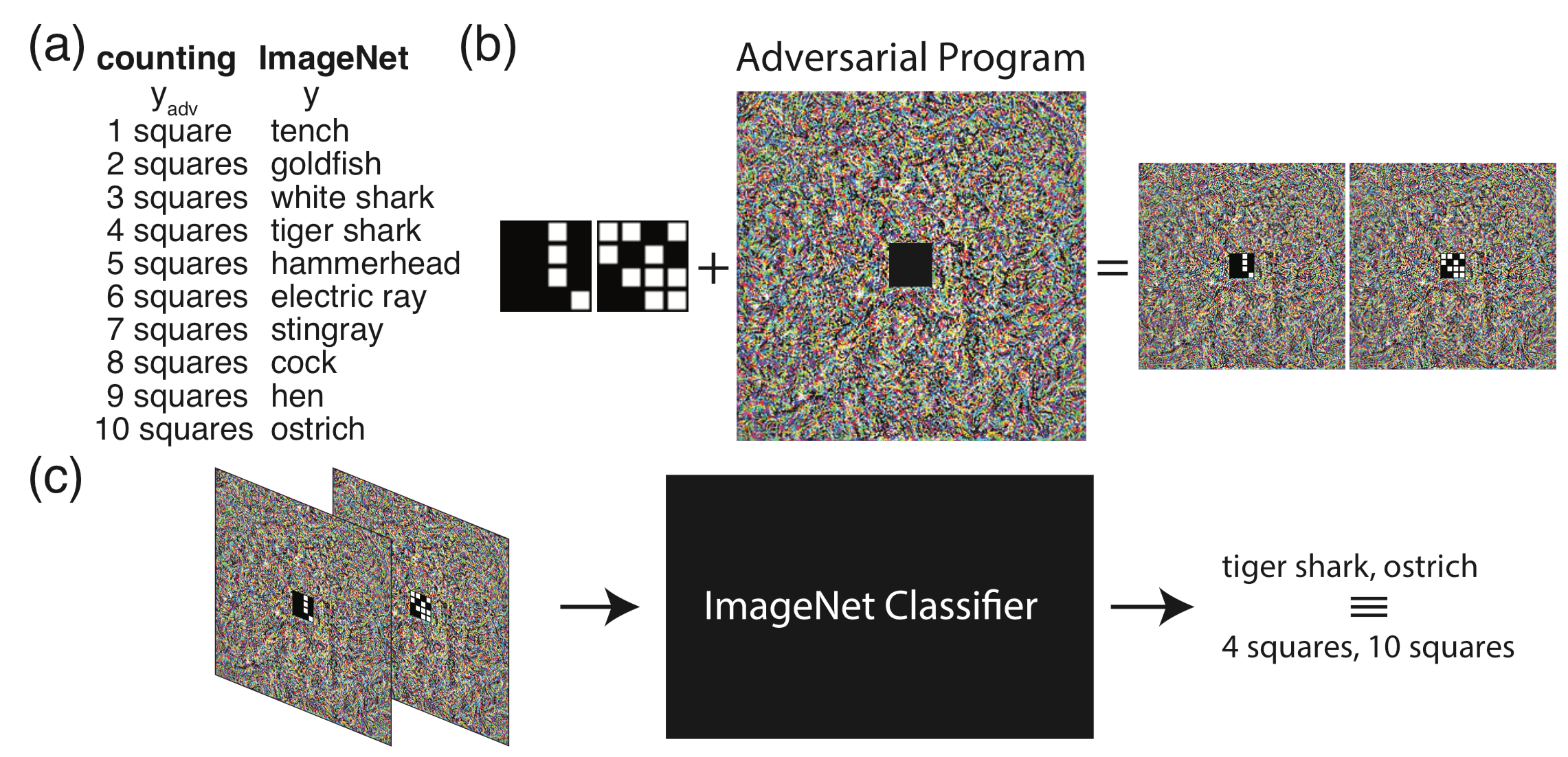
先来看看整个对抗重编程的流程
在a中,我们将imagenet任务的输出标签映射到对抗任务的标签,这里我们给定的对抗任务是计算小图像中的格子数量,所以对抗任务的标签为1~10;在b中,将对抗任务的小图像嵌入到对抗程序的中间,从而得到对抗图像。在c中,当把对抗图像输入分类器时,分类器此时会输出标签tiger shark,ostrich等,不过由于有hf函数的存在,他们会被映射到对应的4,10等。经过这一套流程,我们对一个在imagenet上训练的分类模型进行了对抗重编程攻击,使它的任务变为数格子。
原理
我们设一个经过训练的模型,其原本的任务是,给定输入x,会得到输出f(x)
现在有一个攻击者,其对抗任务是对于给定的输入x~,会得到输出g(x~),这里x~和x不一定需要是同域的。
这看起来是不可行的,但是攻击者通过学习对抗重编程函数hf(.;θ)和hg(.;θ)来实现这两个任务之间的映射。
hf(.;θ)用于将输入从x~所在的域转换到x所在的域,也就是说,经过hf的处理后得到的hf(x~;θ)对于f而言是有效的输入;而hg则将f的输出f(h(x~;θ))映射会g(x~)的输出。这里对抗程序的参数θ会被调整以满足:
这里为了简单起见,我们将x~定义为小图像,g为处理小图像的函数,x为大图像,f为处理大图像的函数。hf函数的作用则是在大图像的中心进行修改,hg则是在输出标签之间一个简单的硬编码的映射函数。事实上,hf (hg)可以是任何一致的转换,在两个任务的输入(输出)格式之间转换,并让模型执行对抗任务。
在整个攻击中,我们将对抗程序定义为:
其中
是需要学习的对抗程序参数,n是imagenet图像的宽,M是掩码矩阵,对于对抗任务对应的对抗数据的图像位置的值为0,否则为1
上面的式子中我们用了tanh,这是为了将对抗扰动限定在(-1,1)范围内,这与目标模型训练分类的重缩放后的ImageNet图像相同
设
是我们执行对抗任务所用的样本,其中k<n
则是和Imagenet图像同样大小的图像,x~被放置在了通过M定义的合适的区域。
所以对应的对抗图像为:
设P (y|X)为目标模型给定输入图像X,ImageNet图像的标签y∈{1,…, 1000}。我们定义一个硬编码的映射函数hg (yadv),它将一个标签从一个对抗任务yadv映射到一组ImageNet标签。例如,如果一个对抗任务有10个不同的类(yadv∈{1,…10},hg(·)可以定义为将ImageNet的前10个类、任何其他10个类或多个ImageNet类映射给对抗标签。
因此,我们的对抗目标是使P (hg (yadv)|Xadv)的概率最大化。我们把最优化问题设为
其中λ是权重范数惩罚项的系数,以减少过拟合。用Adam优化器优化损失。
注意,优化之后,对抗程序对于攻击者而言有最小的对抗损失,因为它只需要计算Xadv,并将得到的ImageNet标签映射到正确的类标签。换句话说,在推理过程中,攻击者只需要存储程序并将其添加到数据中,从而将大部分计算留给目标模型。
这里还有一种需要注意的是,这种攻击方式必须要利用目标模型的非线性行为,这和传统的对抗样本的攻击不同,它们是基于对模型的线性逼近,从而造成高的错误率。假设存在一个线性模型,它接收输入x~以及连接到单个向量x的θ :
假设线性模型的权重分为两部分,即:
则模型的输出为:
从上式可以看到,对抗程序θ对偏置起作用,但是却没用应用于x~的权重。
因此,对抗程序θ可以使模型始终输出一类或另一类,但不能改变输入x的处理方式。为了实现对抗性重编程,模型必须存在x̃和θ之间的非线性相互作用。而非线性的深度学习模型恰好满足这一点。
实验分析
这里为了验证对抗重编程是可行的,设计了三种对抗任务,分别是数格子、MNIST分类和CIFAR10分类
数格子:
正如在对抗重编程的流程图中看到的一样,生成了尺寸为36 × 36 × 3的图像(x̃),其中包括9 × 9个带有黑色框架的白色方块。每个正方形可以出现在图像中的16个不同的位置,正方形的数量从1到10。这些方块被随机放置在网格点上。我们将这些图像嵌入到一个对抗程序,得到的图像(Xadv)大小为299 × 299 × 3,中间的方格为36 × 36 × 3。我们为每个ImageNet模型训练一个对抗程序,使前10个ImageNet标签代表每幅图像中的正方形数量。注意,在ImageNet中使用的标签与新的对抗性任务的标签没有关系。例如,“White shark”与图像中的3个方块数无关,而“Ostrich”与10个方块一点也不相似。
MNIST分类:
与数格子任务类似,将大小为28 × 28 × 3的MNIST数字嵌入到对抗程序中,我们将前10个ImageNet标签分配给MNIST数字,并为每个ImageNet模型训练一个对抗程序。下图是应用于每个网络的对抗程序的示例。
CIFAR-10分类:
CIFAR10的处理也与MNIST类似,一些对抗图像的实例如下
我们也可以很直观地看到三个任务对于每个模型训练后生成的对抗程序
实验结果总结在表格里了:
表中第二类是数格子、第三列是MNIST分类,第四列是CIFAR10分类,可以看出对抗重编程的攻击效果还是非常好的。
复现
为了直观的理解,会在解释代码的同时打印出对应的变量
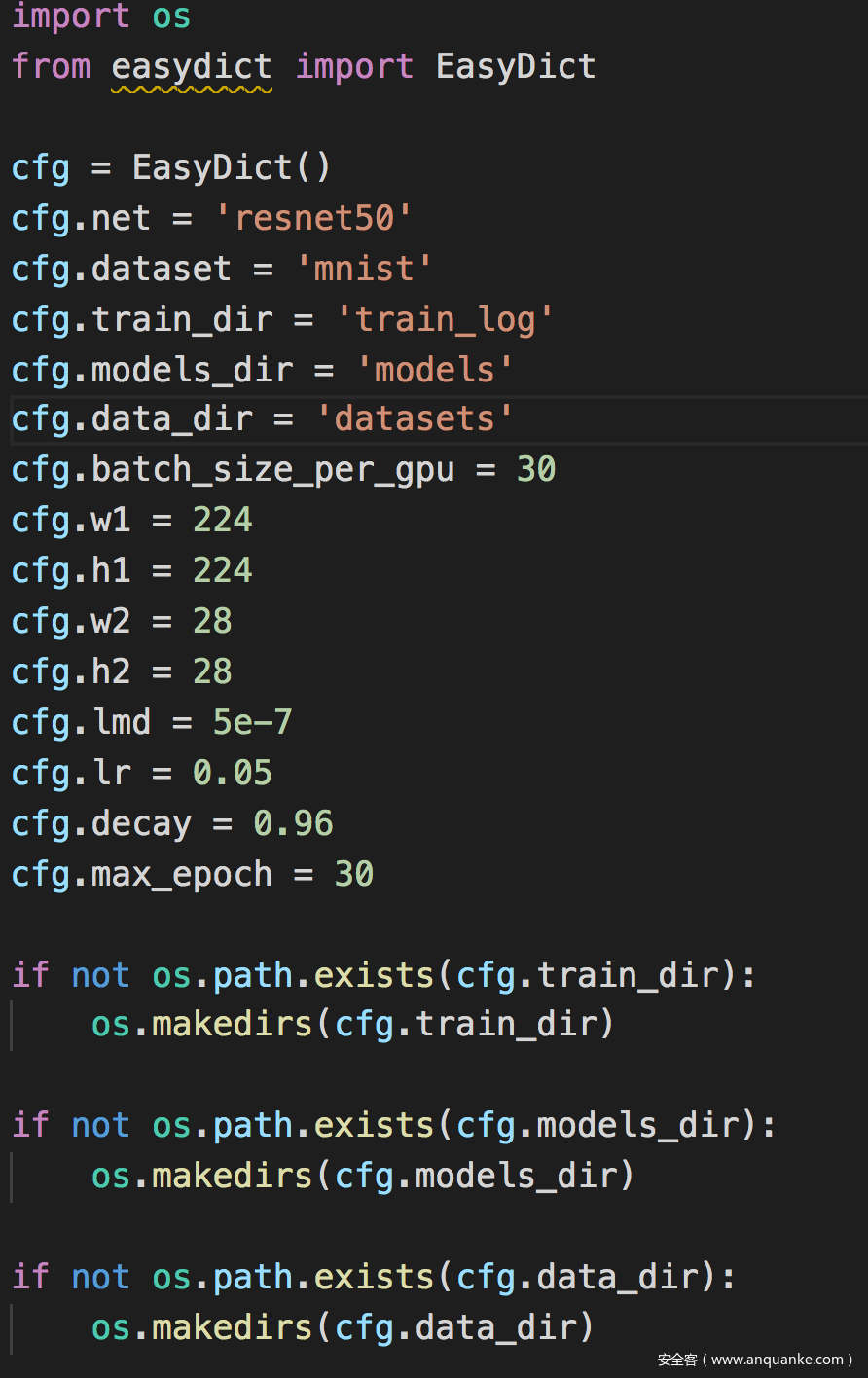
相关配置文件
这里的h1,w1是大图像,即imagenet图像的尺寸,h2,w2是对抗任务所用的小图像的尺寸。
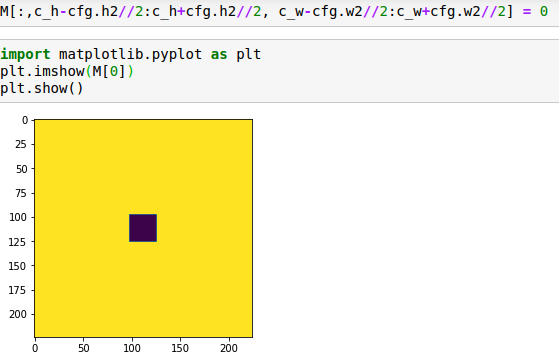
初始化掩码,即前面提到的M
使用imagenet标签的前10个作为对抗任务的标签
最关键的是compute_loss函数以及forward函数
compute_loss函数如下
正如前面提到的,这里的损失由两项组成,第一项是正常训练损失,第二项是权重惩罚项,这里用的是l2范数,lmd是系数,已经在配置文件中定义了
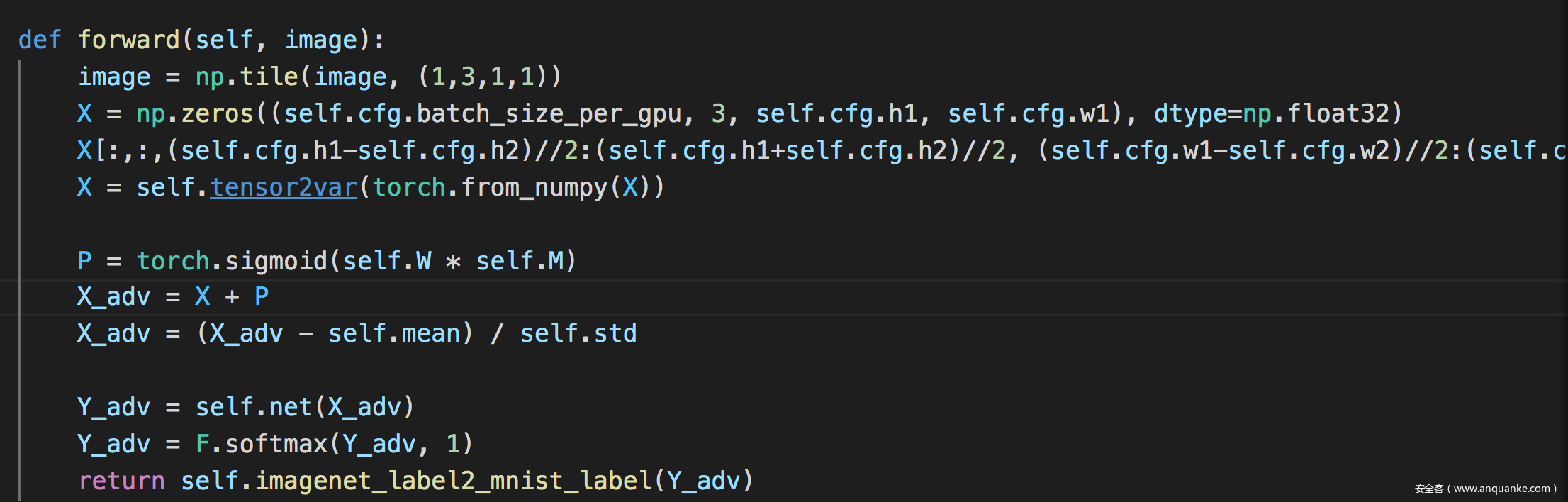
forward函数如下
为了方便理解,我们一步步打印出看看
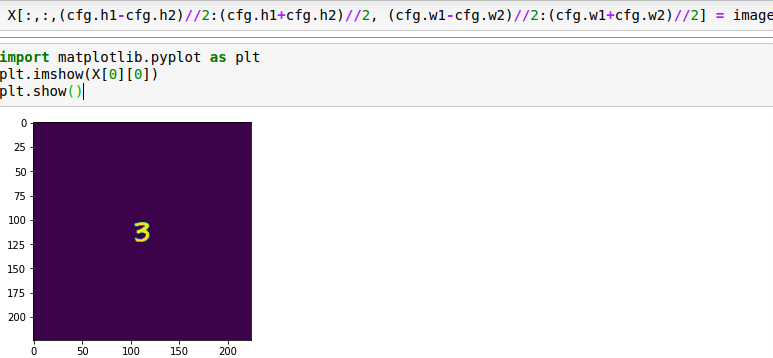
首先是image,也是论文中提到的x~
论文中的X通过代码实现的:
在目标模型上生成的对抗程序,即P
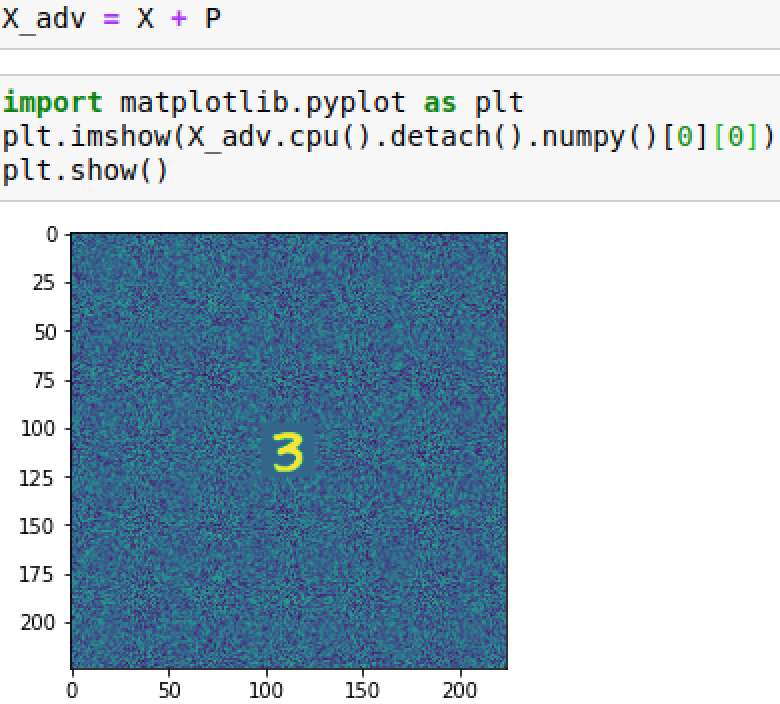
X+P得到对抗图像
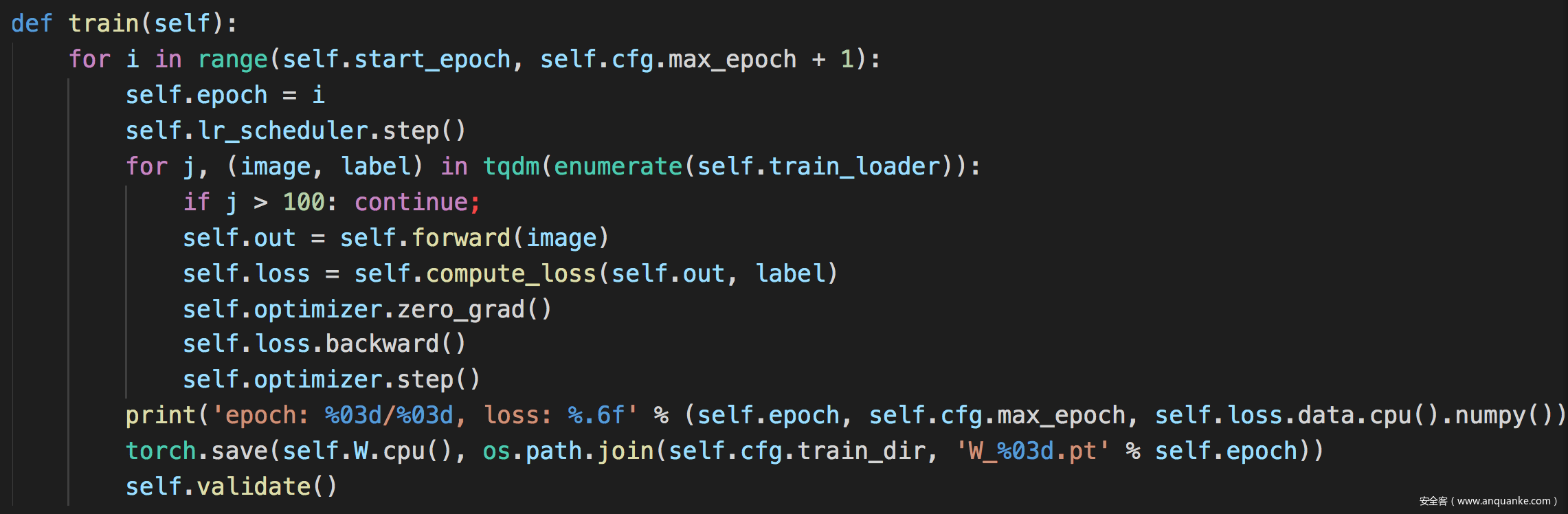
训练函数
可以看到self.out是由self.forward返回的,这里就是训练部分。
训练过程运行如图
我们先来看看在原模型上进行测试时的效果
然后是在训练后的模型上测试的效果
可以看到确实成功率提高了不少。
这里的对抗重编程攻击针对的还只是计算机视觉的分类任务,在其他领域的也有研究人员进行了分析,包括参考文献中的2.3对自然语言处理中的应用进行了研究。此外还有研究人员详细分析了对抗重编程可以成功进行攻击的条件以及背后的原因,详见参考文献4.
此外,通过本文的介绍,师傅们应该隐隐约约看出来,这种攻击范式有对抗样本、后门攻击、UAP的影子,这方面的结合点还是很有意思的。
参考
1.Elsayed G F, Goodfellow I, Sohl-Dickstein J. Adversarial reprogramming of neural networks[J]. arXiv preprint arXiv:1806.11146, 2018.
2.Neekhara P, Hussain S, Dubnov S, et al. Adversarial reprogramming of text classification neural networks[J]. arXiv preprint arXiv:1809.01829, 2018.
3.Hambardzumyan K, Khachatrian H, May J. Warp: Word-level adversarial reprogramming[J]. arXiv preprint arXiv:2101.00121, 2021.
4.Zheng Y, Feng X, Xia Z, et al. Why Adversarial Reprogramming Works, When It Fails, and How to Tell the Difference[J]. arXiv preprint arXiv:2108.11673, 2021.


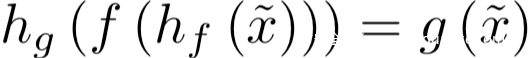
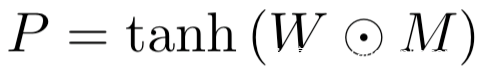
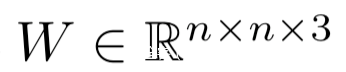
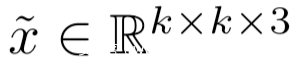
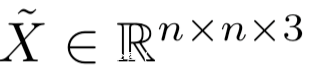
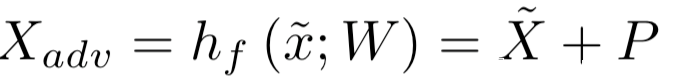
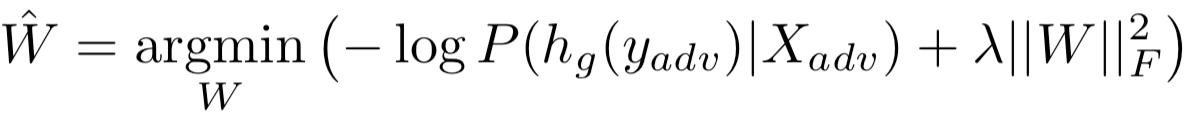
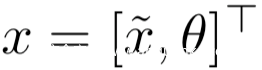
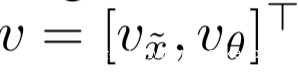


















发表评论
您还未登录,请先登录。
登录