前言
目前,图结构的数据被应用于各种安全敏感领域(例如恶意软件分析,内存取证,欺诈检测,药物发现等),而随着图神经网络的兴起,研究人员尝试将图神经网络应用于这类数据上实施分析,发现都能达到非常先进的水平。在这种趋势下,图神经网络是否安全,便是安全研究人员关注的重点,本文分析并复现首次实现针对图神经网络进行后门攻击的研究工作,该工作发表于安全四大之一的USENIX Security 2021,它将提出的攻击命名为GTA。
基础
特点
同样是后门攻击,图上的后门攻击有哪些特点呢?
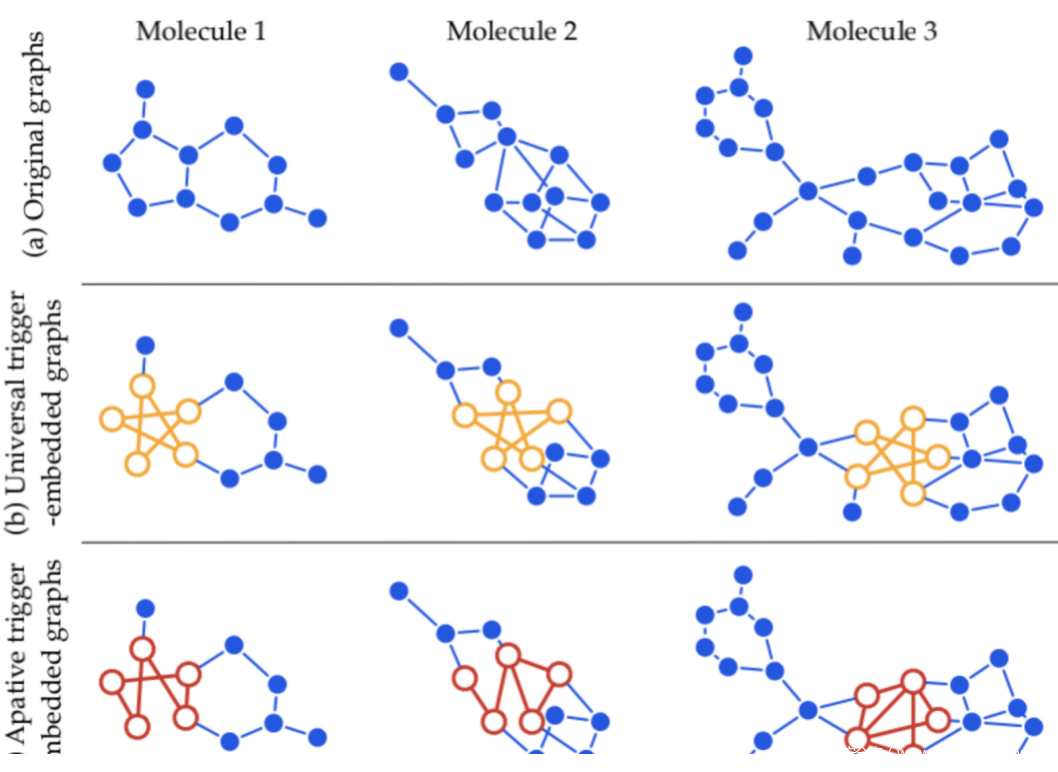
目前的后门攻击基本是在图像领域展开研究的,与结构化、连续的数据(如图像)不同,图数据本质上是非结构化和离散的,需要具有相同性质的查询触发器。GTA将触发器定义为特定的子图,包括拓扑结构和描述(节点和边)特征,这为攻击者提供了一个大的设计范围。此外GTA不是为所有图定义一个固定的触发器,而是根据单个图的特征生成触发器,这优化了攻击的有效性(例如,误分类置信度)和规避性(例如,扰动幅度)。如下所示,第三行是被GTA植入触发器后的图,图中红色的子图是触发器,可以看到,每个图的触发器都是不同的。
总的来说,GTA本质上也是要生成一个木马GNN,训练该模型时的核心是双层优化,对木马GNN和触发器生成器的参数进行轮流优化,但是由于假设攻击者没有访问下游分类器的能力,因此优化的目标是针对它们的潜在表达形式(embedding)的L2距离,即要保证正常GNN和木马GNN在干净输入时要保证较为相似的潜在表达输出,也要保证木马GNN在带有木马的输入(非攻击目标类)和目标类干净输入时较为相似的潜在表达输出。
我们知道,GNN被应用的领域可以被简单的分为两类,分别是inductive task和transductive task,前者的代表性任务就是图分类,后者的代表性任务就是节点分类。而GTA对两者都可实施攻击。
Inductive task和Transductive task
这里我们顺便再提一下inductive task和transductive task的区别与联系。
inductive task翻译成中文可以叫做“归纳式学习”,顾名思义,就是从已有数据中归纳出模式来,应用于新的数据和任务。我们常用的机器学习模式,就是这样的:根据已有数据,学习分类器,然后应用于新的数据或任务
transductive task翻译成中文可以叫做“直推式学习”,指的是由当前学习的知识直接推广到给定的数据上。其实相当于是给了一些测试数据的情况下,结合已有的训练数据,看能不能推广到测试数据上
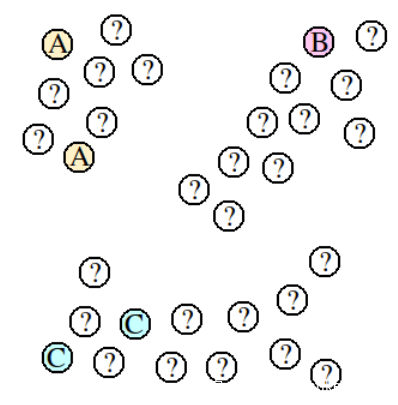
我们以下图为例,可以更直观地进行解释
设现在的任务是:已知ABC的类别,求问号的类别
inductive learning就是只根据现有的ABC,用比如kNN距离算法来预测,在来一个新的数据的时候,还是只根据5个ABC来预测;而transductive learning直接以某种算法观察出数据的分布,这里呈现三个cluster,就根据cluster判定,不会建立一个预测的模型,如果一个新的数据加进来就必须重新算一遍整个算法,新加的数据也会导致旧的已预测问号的结果改变。
图神经网络GNN
GNN以图G为输入,包括其拓扑结构和描述特征,并为每个结点v生成表示(embedding) $z_v$,设Z表示矩阵形式的节点嵌入。
我们考虑一个基于领域聚合范式的GNN:
其中,Z(k)是第k次迭代后的节点嵌入,同时也是传递给邻居节点的message,而aggregation 函数则依赖于来自上一次迭代的邻接矩阵A、可训练的参数、以及节点嵌入Z(k-1)
通常Z(0)被初始化为G的节点特征。为了得到图嵌入$z_G$,readout函数会集合来自最后一次迭代K的节点嵌入:
总的来说,GNN建模了一个函数f,为G生成了$z_G$=f(G)
预训练GNN
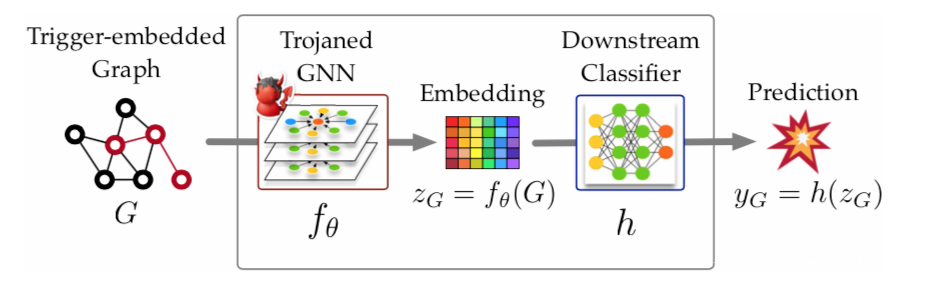
对于有标签数据非常稀疏或者训练非常昂贵的领域来说,使用预训练模型是非常好的选择。在迁移学习的环境下,如下所示,一个预训练的GNN f与下游的分类器h一起组成了端到端的系统
举例而言,对于一个化学药物分类任务,给定一个分子的图G,首先将其映射到其嵌入$z_G$=f(G),然后进行分类$y_G=h(z_G)$
与f相比,h明显更简单(比如就是一个全连接层)。注意,训练f的数据往往与下游任务不同,但具有相似的特征(例如,一般分子与有毒分子)。经常有必要对系统进行微调。可以选择执行full-tuning来同时训练f和h,或者只训练h但f固定的partial-tuning。
威胁模型
我们假设的威胁模型如上图所示,给定一个预训练的GNN $f{\theta_0}$,攻击者在不修改架构的同时修改参数伪造一个GNN $f\theta$
我们假设敌手有能力接触到下游任务所用的数据集。在将$f_\theta$和下游分类器h集成为一个端到端系统后,用户会进行微调以满足下游任务。为了让攻击更实际,我们假设攻击者不知道用户使用的分类器h的情况,也不清楚是如何微调系统的。
GTA攻击
我们以图分类任务为例来说明。
给定一个预训练GNN $\theta_0$,攻击者希望伪造一个木马模型$\theta$,它会让系统对嵌入了触发器的图误分类为指定的类$y_t$,而在正常的图上是正常的分类
我们将触发器设计为子图$g_t$(包括拓扑结构和描述特征),并设计一个mixing 函数m(.;$g_t$),用于将图G和触发器$g_t$混合从而生成一个嵌入了触发器的图m(G;$g_t$)
因为攻击者的目标可以定义为:
h是微调后的下游的分类器,G代表的是任务中的任意图。直观上,第一个目标规定了所有触发器嵌入图都被误分类为目标类(即攻击有效性),第二个目标则保证了原始gnn和木马gnn在良性图上的行为是不可区分的(即攻击规避性)。
不过通过上式来寻找最优的触发器和木马模型是non-trivial的:
•由于攻击者无法访问下游模型h,直接根据上式优化$g_t$和$ \theta$是不现实的。
•由于$g_t$和$ \theta$的相互依赖,每次更新$g_t$都需要对$ \theta$进行昂贵的计算。
•存在多种组合方式,这意味着存在一个禁止性搜索空间。
•对所有图使用通用触发器$g_t$忽略了单个图的特征,易于被检测。
为了解决以上问题
1.我们不是将$g_t$和$ \theta$与最终预测相关联,而是根据特征表示对它们进行优化;
2.采用双层优化公式,$g_t$作为超参数,$ \theta$作为模型参数,交叉优化;
3.mixing函数m作为一个有效的替换算子,在G内找到并替换与$g_t$最相似的子图g;
4.我们引入了自适应触发器的概念,即$g_t$对每个给定的图G进行特别优化(每个图G都会得到一个特定的gt)。
接下来我们分别介绍双层优化问题、mixing函数、以及触发器生成等攻击的关键部分
双层优化问题
我们已经知道,攻击者从下游任务数据集取样得到的数据由实例(G,$y_G$)组成,G是图,$y_G$是标签
我们使用$g_t$和$ \theta$分别作用upper-level和lower-level变量来构建bi-level 优化目标
上式中,$l{atk}$和$l{ret}$分别代表量化攻击有效性和准确性保持的损失项,对应于我们前面定义的目标
因为无法访问分类器h,我们不再将$l{atk}$和$l{ret}$与最终预测关联,而是根据潜在表示(latent representation)定义它们。
我们把数据集Dfen为两部分,D[$y_t$]是目标类t的图,D[\$y_t$]是其他类的图
$l{atk}$确保$f \theta$会为D[$y_t$]以及D[\$y_t$]中嵌入了触发器的图生成相似的嵌入
而$l{ret}$则确保$f \theta$和$f_ {\theta0}$为D中的图生成相似的嵌入,即满足如下公式
其中$ \triangle$用于衡量嵌入的不相似度,在我们的实验中可以使用L2距离
不过准确求解上式的代价是非常昂贵的,由于是bi-level公式,每当$g_t$被更新,就需要重新计算$ \theta$(换句话说,需要在D上重新训练f)
所以我们提出了近似的求解算法,通过在$l{atk}$和$l{ret}$上交替执行梯度下降来迭代优化$g_t$和$ \theta$
在第i次迭代时,给定当前的触发器g^{(i-1)}t以及模型$ \theta^{i-1}$,我们首先通过固定g^{(i-1)}_t,在$l{ret}$上执行梯度下降计算$ \theta^{(i)}$。在实际操作中,这一步会运行$n{io}$次迭代,这个参数代表的是inner-outer optimization ratio,用于平衡$l{atk}$和$l{ret}$的优化。然后在对$ \theta^{(i)}$执单步梯度下降后通过最小化$l{atk}$得到g^{(i)}_t
对于$g_t$的梯度可以通过下式近似
Mixing 函数
mixing函数满足两个目的:
1.对给定的触发器$g_t$,需要在图G中找到最适合替换的子图g
2.使用$g_t$替换g
这里存在很多组合方法,我们将Mixing function限制为一个有效的替换操作符,也就是说,m(G;$g_t$)会使用$g_t$替换G中的g
为了最大化攻击的规避性,我们最好使用一个类似于$g_t$的子图
因此,我们就有了约束:1.g和gt的size是一样的,比如具有相同数量的节点;2.他们有最小的图编辑距离
在图G中找到与gt相似(子图同构)的子图g是一个NP难的问题,我们采用了基于回溯的算法VF2来满足我们设置的情况。VF2通过映射gt中的下一个节点到G中,并反向操作,由此递归地扩展部分匹配。当我们搜索到最相似的子图时,我们就保持当前最高的相速度并且在部分匹配超过这个阈值时提前终止匹配。
触发器生成
在前面的式子中,我们假设对于所有的图都是应用了统一的触发器,尽管这样实施起来比较简单,但是这儿还存在可以优化的地方:
1.忽略了单个图的性质,并且攻击可能没那么有效;
2.每个嵌入了触发器的图都是共享同样的pattern,这会让其更容易被检测出来
那么是否可以对每个图都生成特定的触发器并能够最大化有效性和规避性呢?
我们设计了一个自适应的触发器生成器函数$ \phi_w(.)$,给定G的子图g,它会生成触发器$g_t$
从high level来看,该函数包括两个关键的操作:1.首先把g中的每个结点i映射到其编码$z_i$,这个编码了g的节点特征和拓扑结构;2.其应用了两个生成器函数,第一个讲g的编码映射到$g_t$的拓扑结构,第二个将g的节点编码到$g_t$的节点特征
怎么编码g的特征和上下文呢?我们使用图注意力机制。给定节点对i,j,我们计算注意力系数$ \alpha_{ij}$,这表示j对于i的重要程度(基于他们的节点特征以及拓扑关系),然后我们应用非线性转换计算其邻居编码的聚合(权重系数就是相应的注意力系数)作为i的编码。我们使用D训练一个注意力网络,在下文中我们将i的编码表示为$z_i$
怎么将g的编码映射到$g_t$?$gt$包括两部分,即拓扑结构和节点特征。给定两个节点i,j以及对应的编码,我们使用参数化的余弦相似度定义它们在$g_t$中的连接度A{i,j}
其中$W_c$是可学习的,$1_P$是指示函数,如果p为真则返回1,否则返回0.如果相似度分数超过0.5则i,j在$g_t$中是相连的
同时,对于g中的节点i,我们定义其在$g_t$中的特征为:
我们将这些可学习的参数都称为w,将g的编码映射到{$Xi$}和{$A{ij}$}作为触发器生成器函数$ \phi_w(g)$
怎么解决g和$g_t$之间的依赖关系?大家可能会发现mixing 函数 g=m(G;$g_t$)和触发器生成器函数$g_t= \phi_w(g)$是相互依赖的。为了解决这个鸡生蛋蛋生鸡的问题,我们交错地更新g和$g_t$
我们随机选择g初始化,在第i次迭代时,我们首先基于i-1次迭代的得到的$g^{(i-1)}$来更新触发器g^{i}_t,然后基于g^{i}_t更新选中的子图g^{i}
整体流程
GTA攻击的整体流程如下所示
在其核心部分(4-6行),交替更新模型$ \theta$,触发器生成器函数 $ \phi_w(.)$以及从每个图中选择的子图g
复现
安装DGL
在进行复现之前,我们先要额外安装一个库:DGL,这是为方便实现图形神经网络模型族而构建的。它提供了消息传递的多功能控制、通过自动批处理和高度调优的稀疏矩阵内核进行的速度优化,以及可扩展到数亿个节点和边的图形的多GPU/CPU训练。
由于DGL分cpu版本和gpu版本,所以安装的时候一定要适配自己的环境.
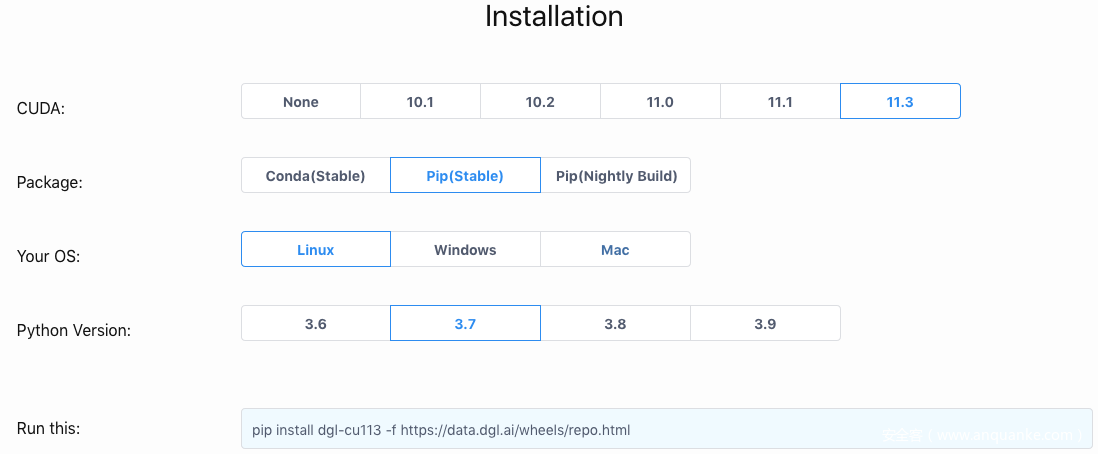
下图是我复现时安装所用的命令
加载数据及训练目标模型
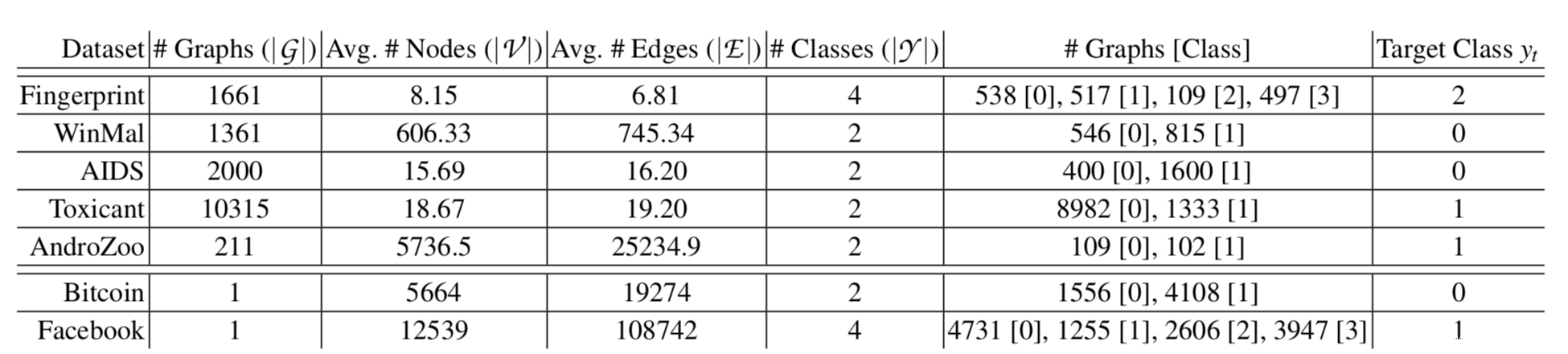
论文提到使用7类公开的安全敏感的数据集,如下所示
表格中,Graphs是指数据集中图的数量,Avg.#Nodes是指平均每个图中的节点数,Avg.#Edge是指平均每个图中边的数量,Classes是指类的数量,Graphs[class]指class类的图的数量,target class则是攻击者选择的攻击目标类
我们这里使用其中之一—AIDS
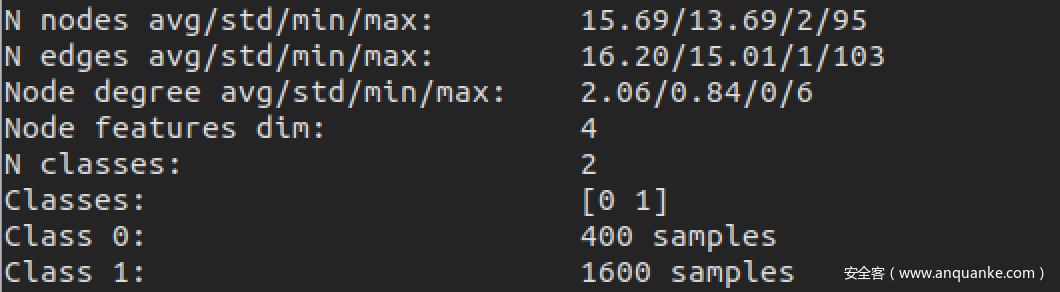
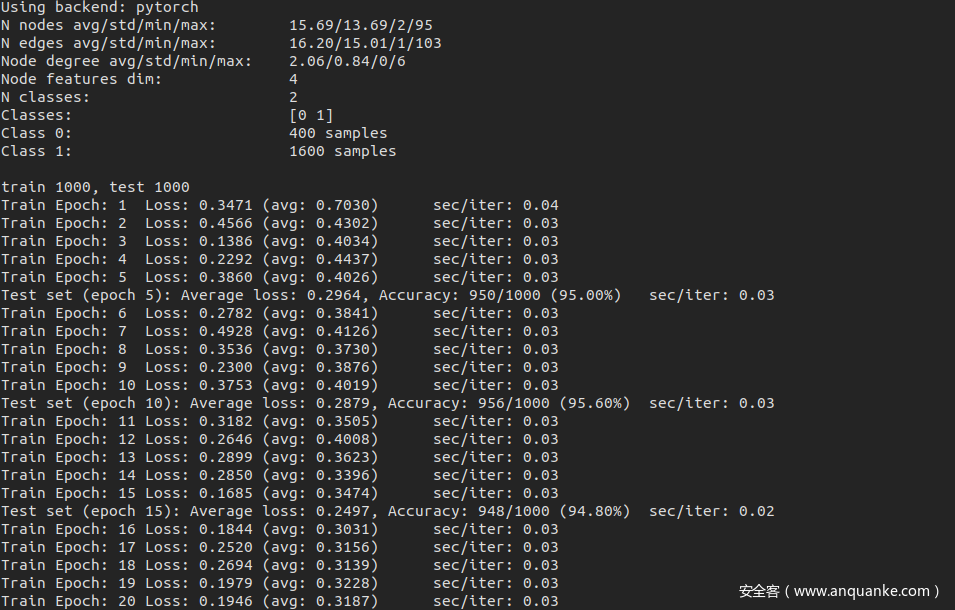
加载数据集后打印相关数据
可以看到和论文给的表格中的值是相符的,说明加载数据这一部分是没问题的
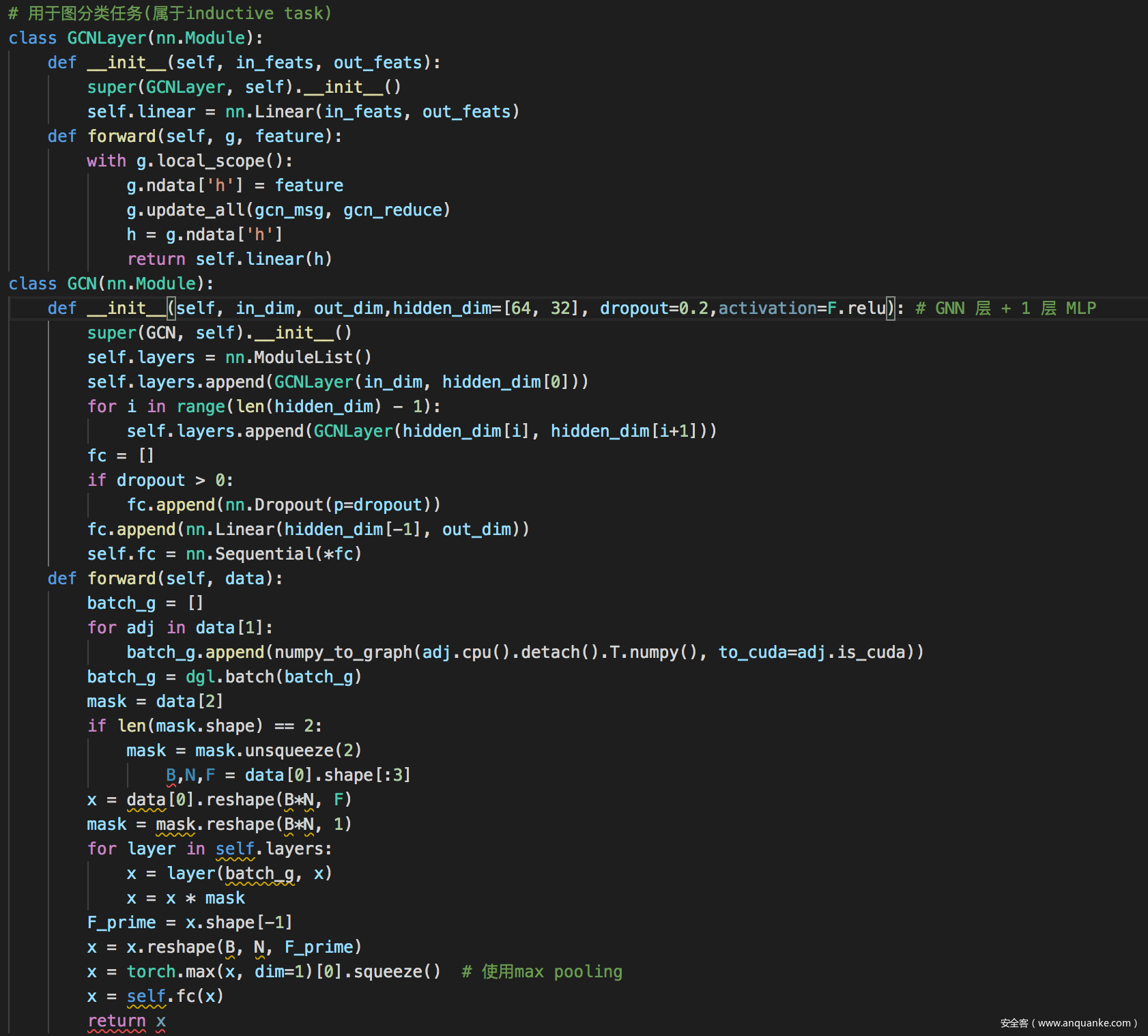
论文中提到可以实现三种SOTA模型,这里我们复现就以GCN为例,代码如下
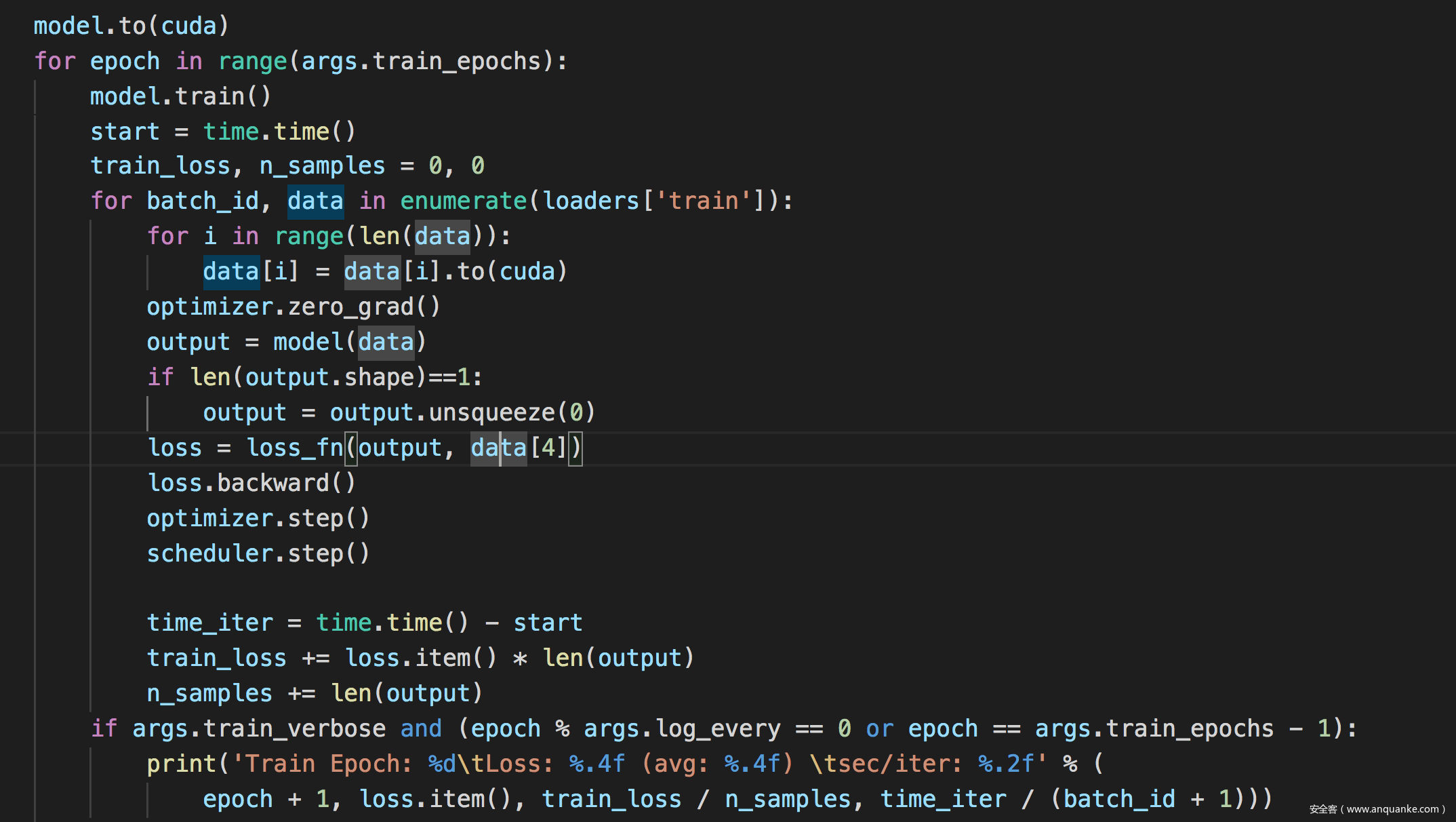
训练模型
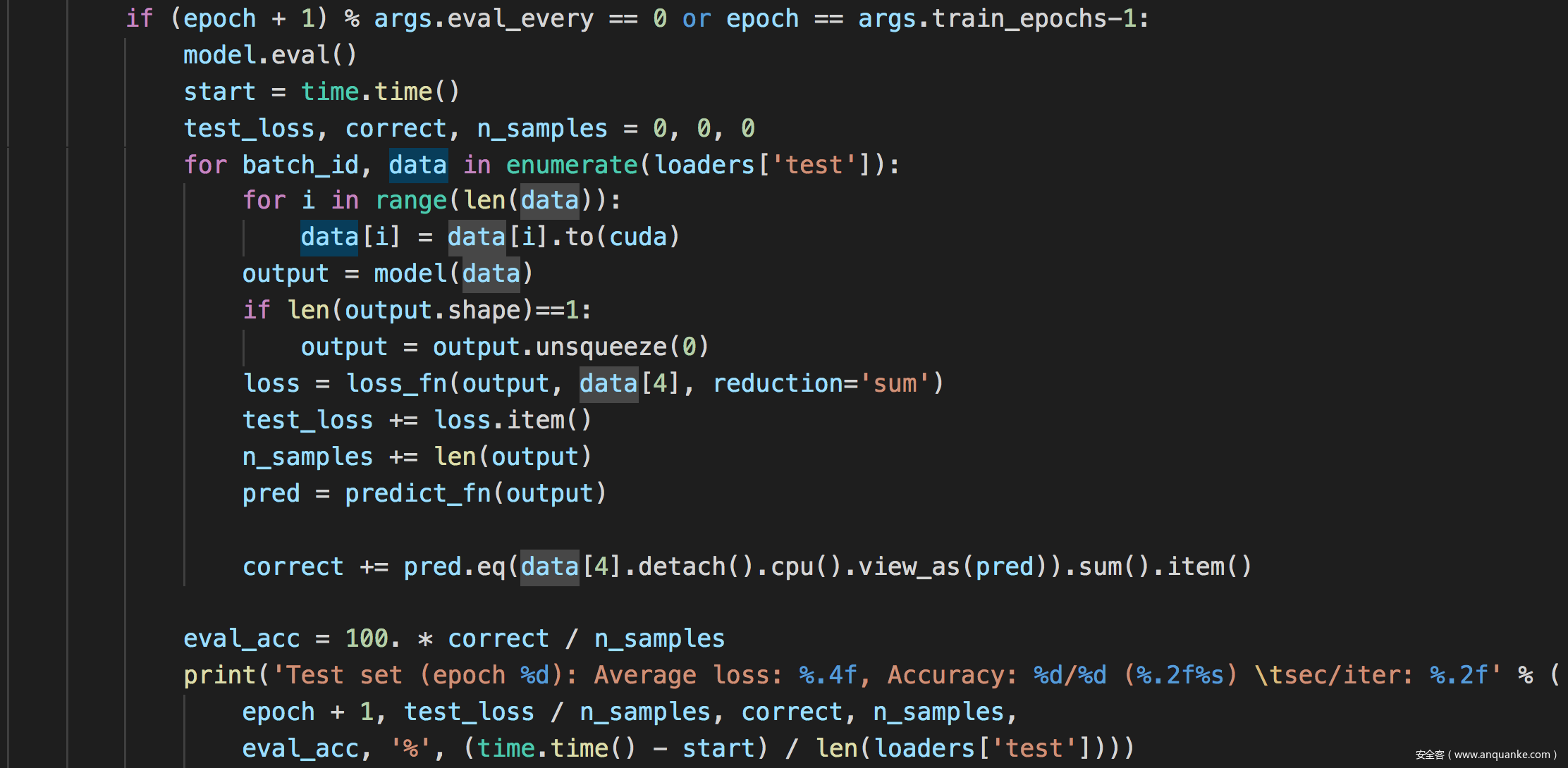
测试模型
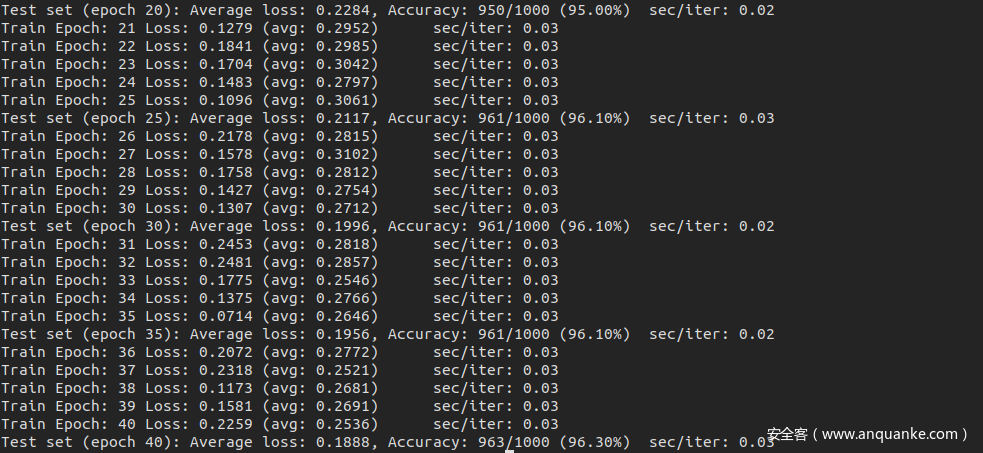
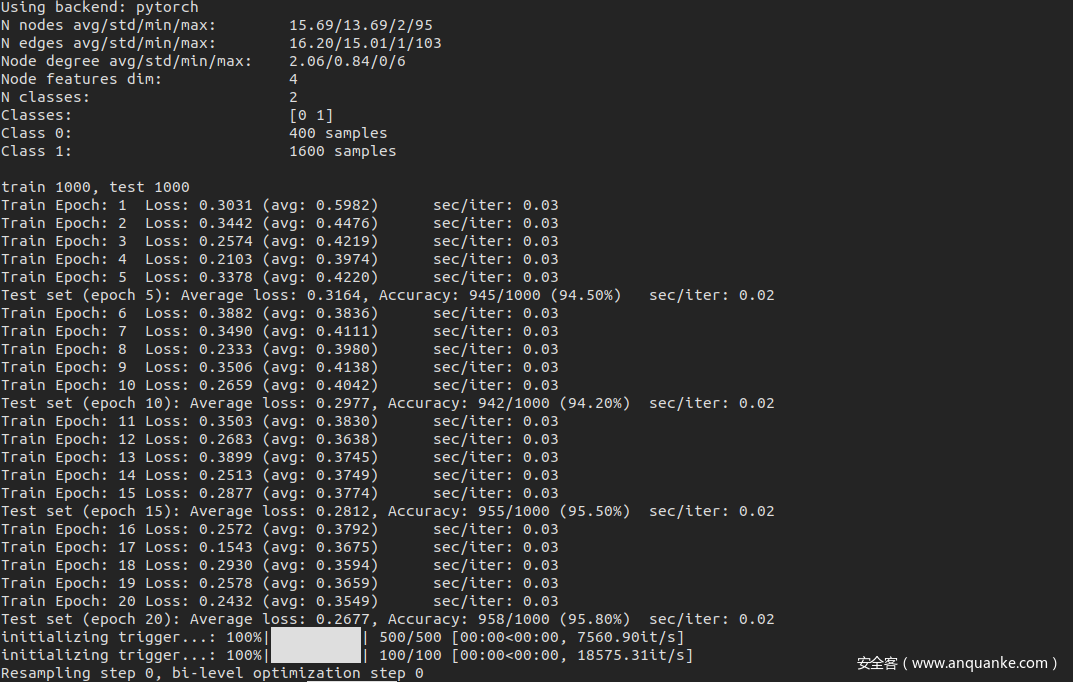
结果如下
可以看到训练了40个epoch之后,准确率达到了96.30%
然后保存该模型,接下里进行后门攻击
后门攻击
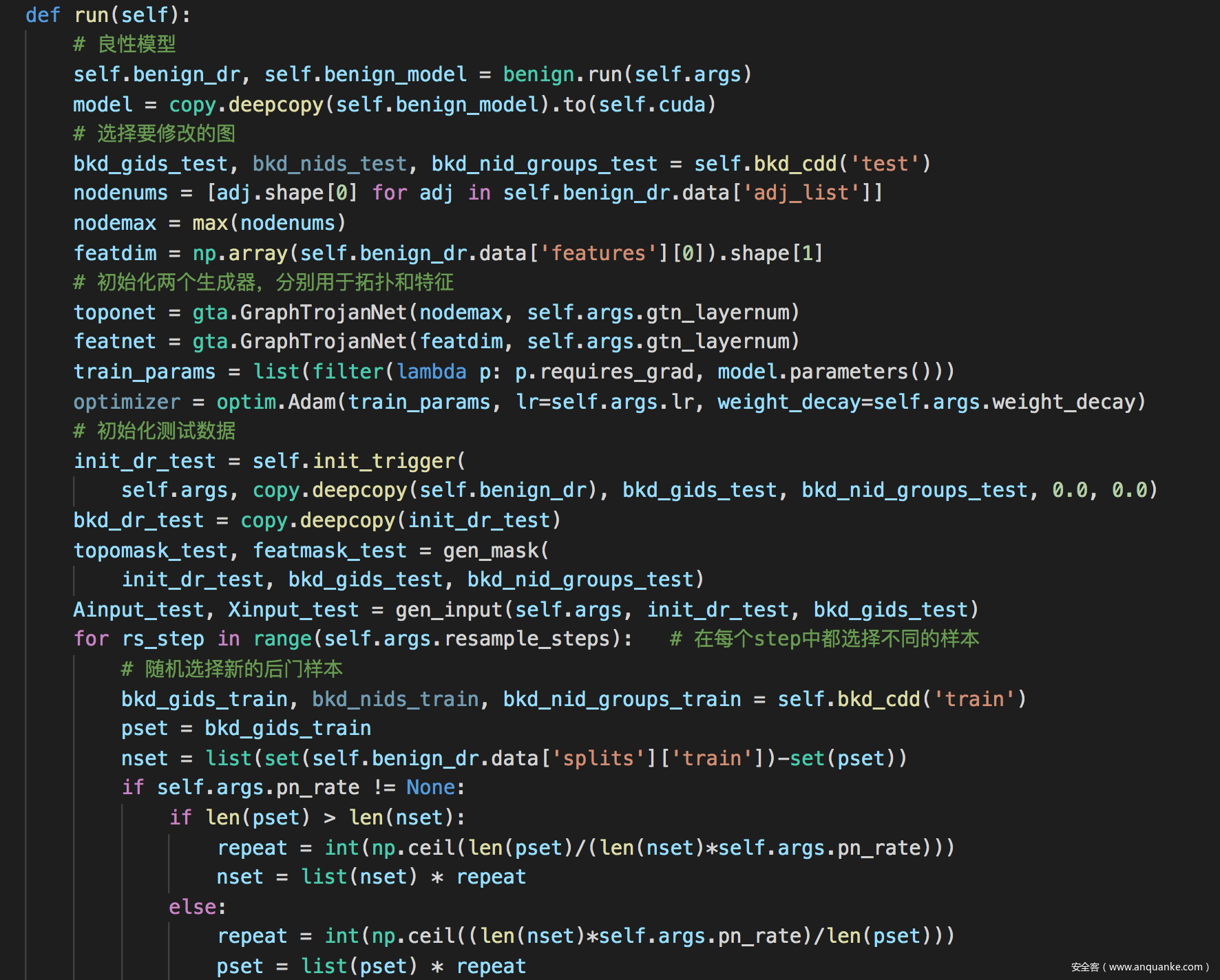
主体代码
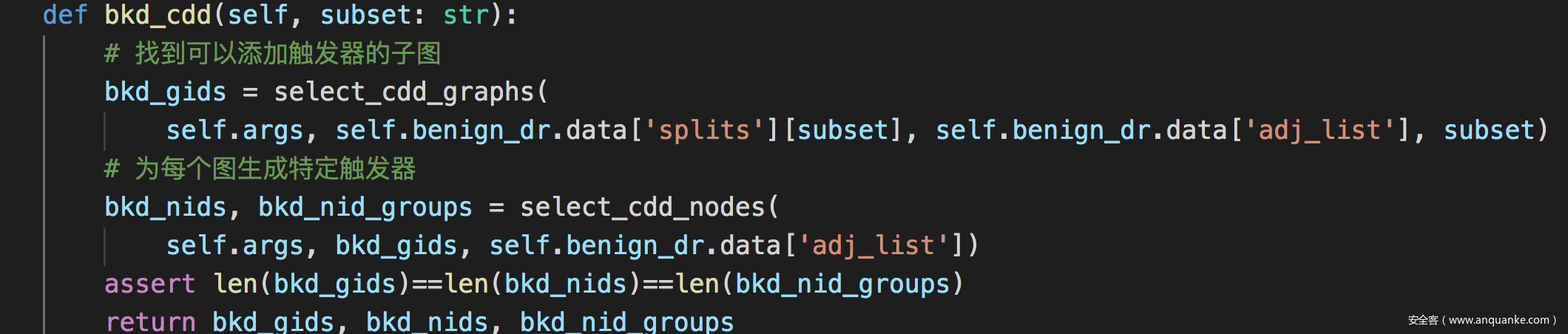
生成触发器
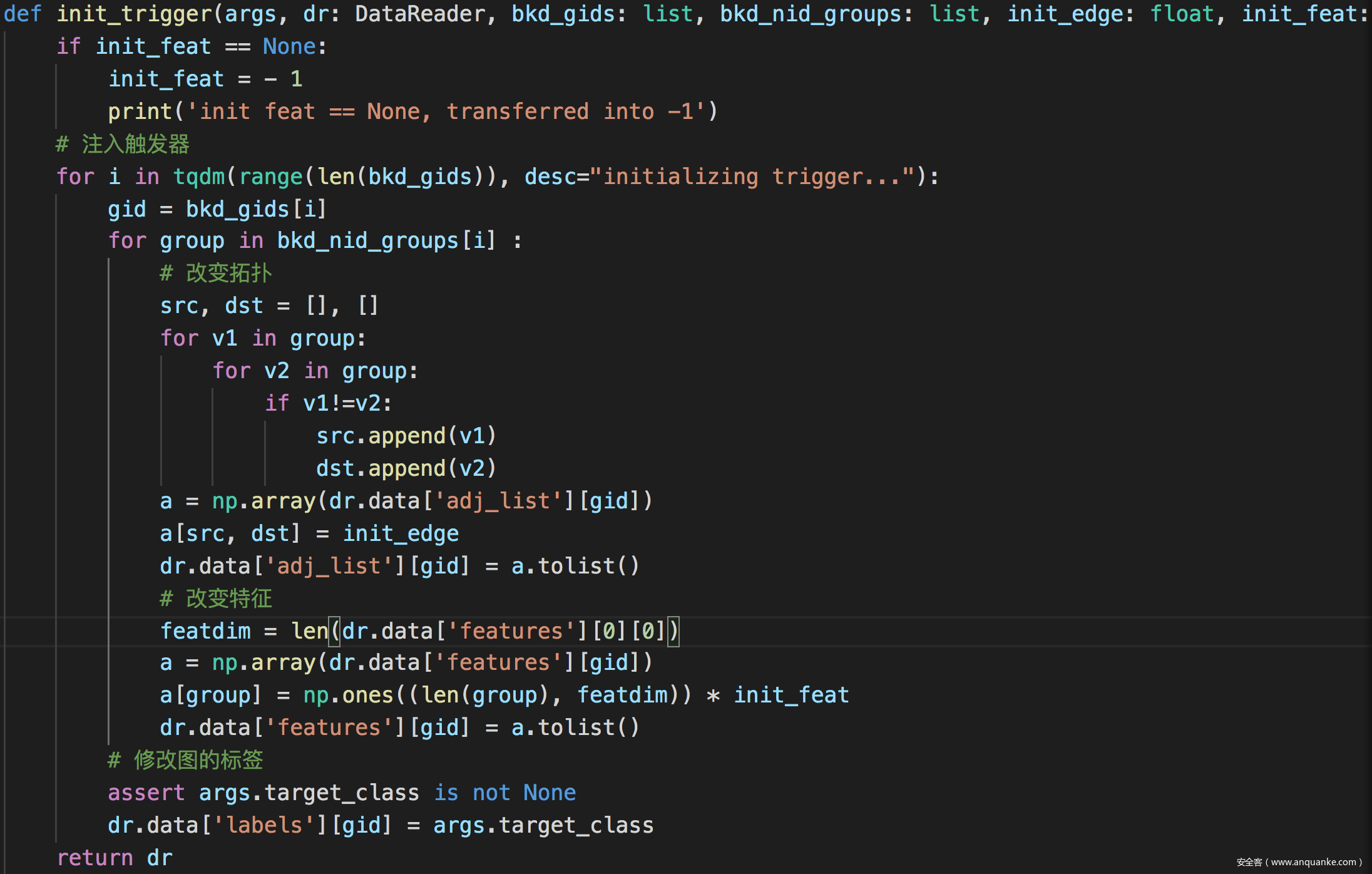
注入触发器
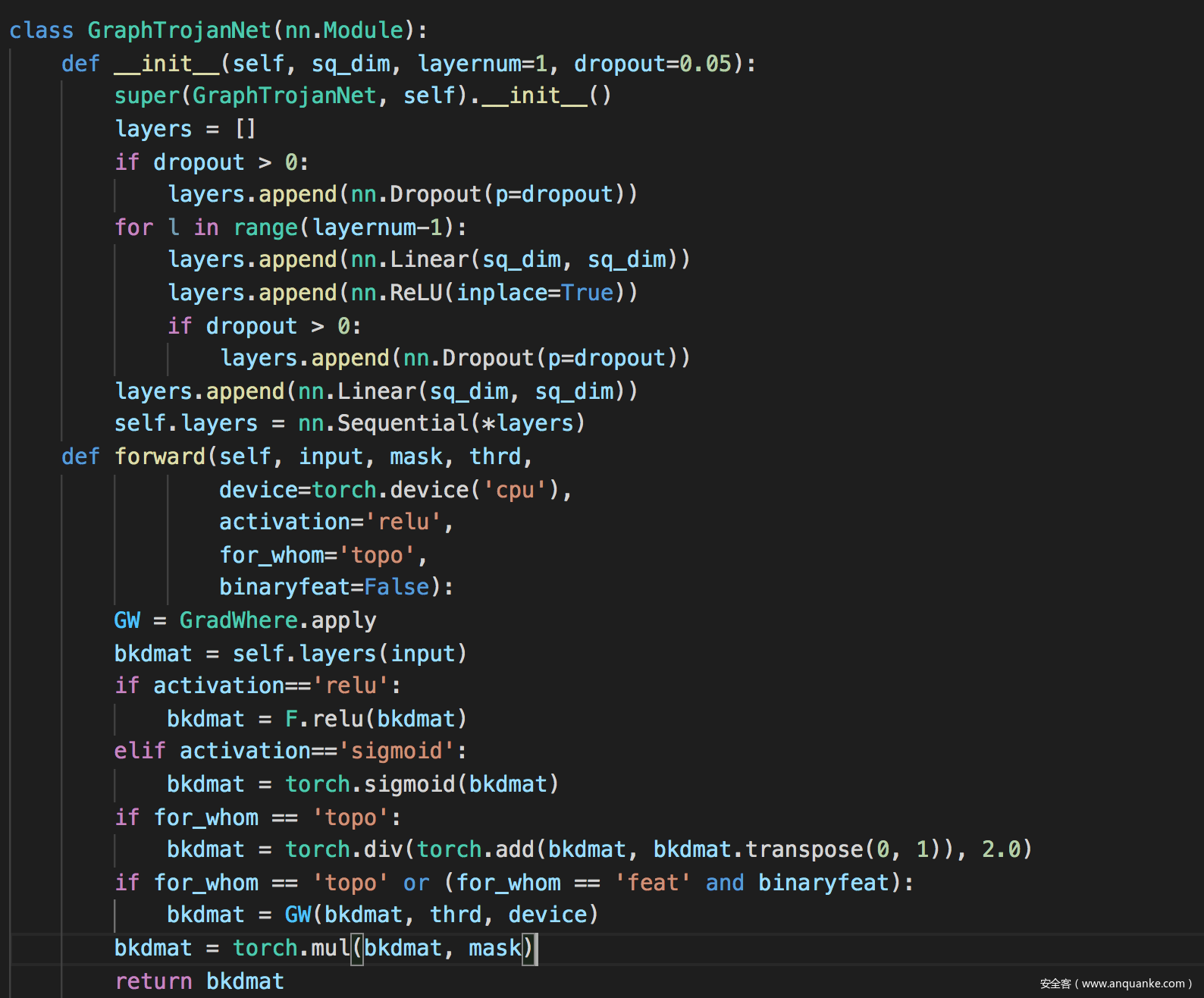
其中还有一些关键的地方,包括生成器的代码实现
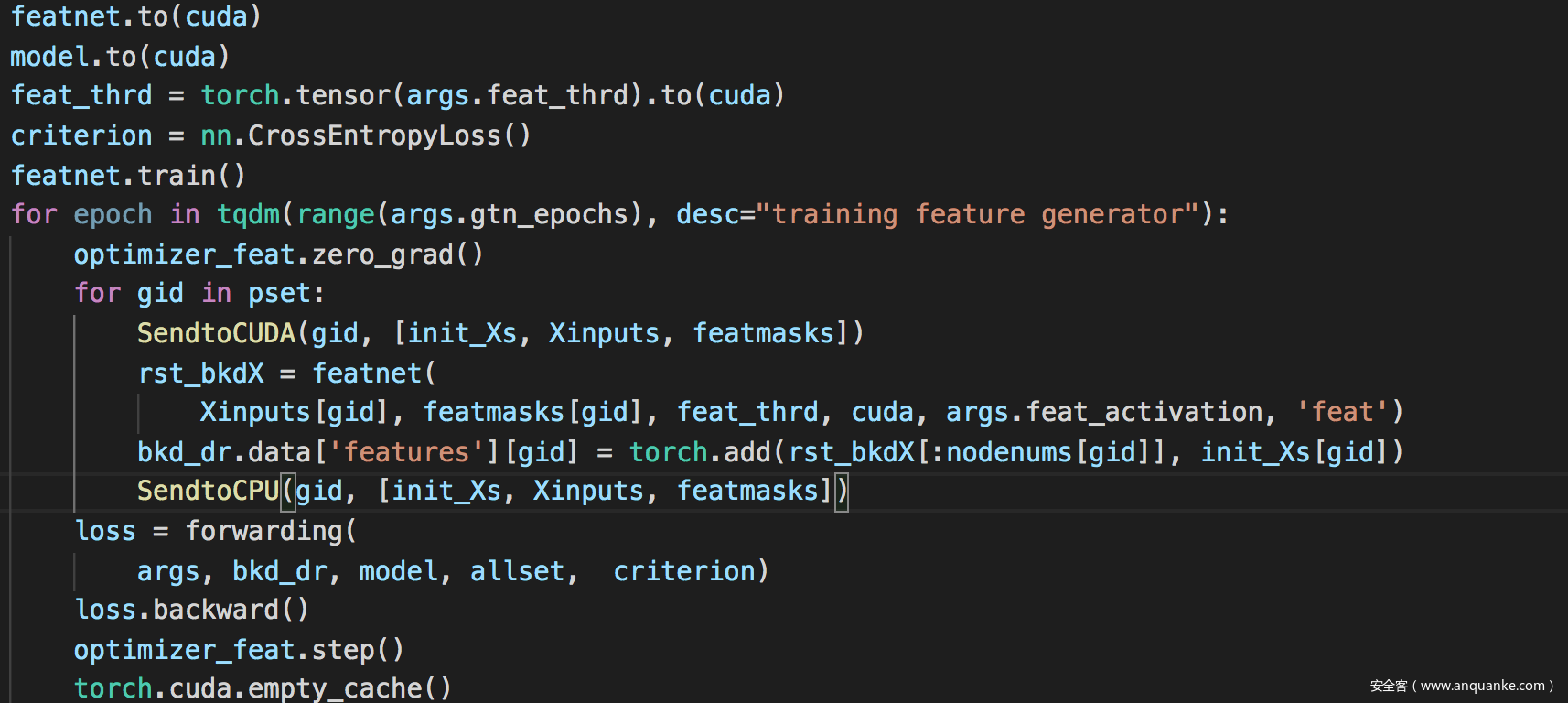
以及训练生成器的代码实现
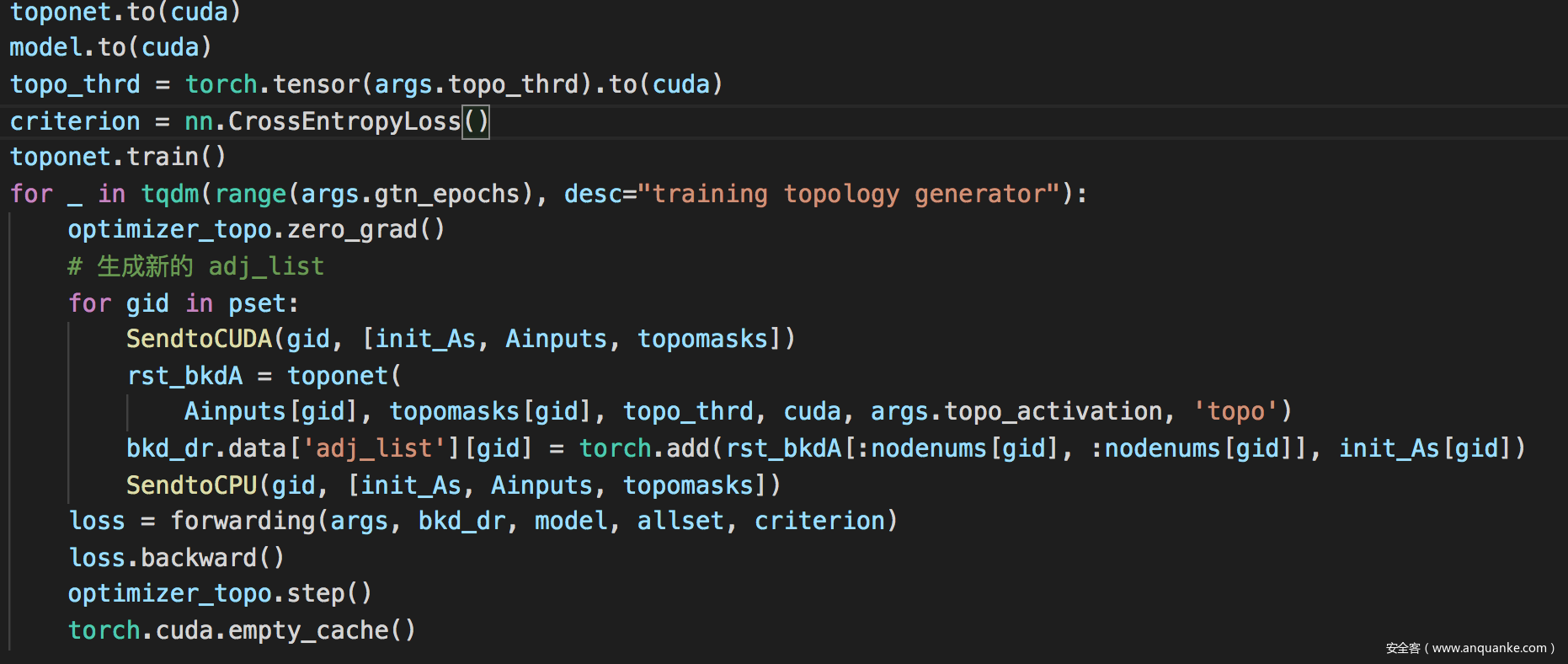
训练拓扑生成器
训练特征生成器
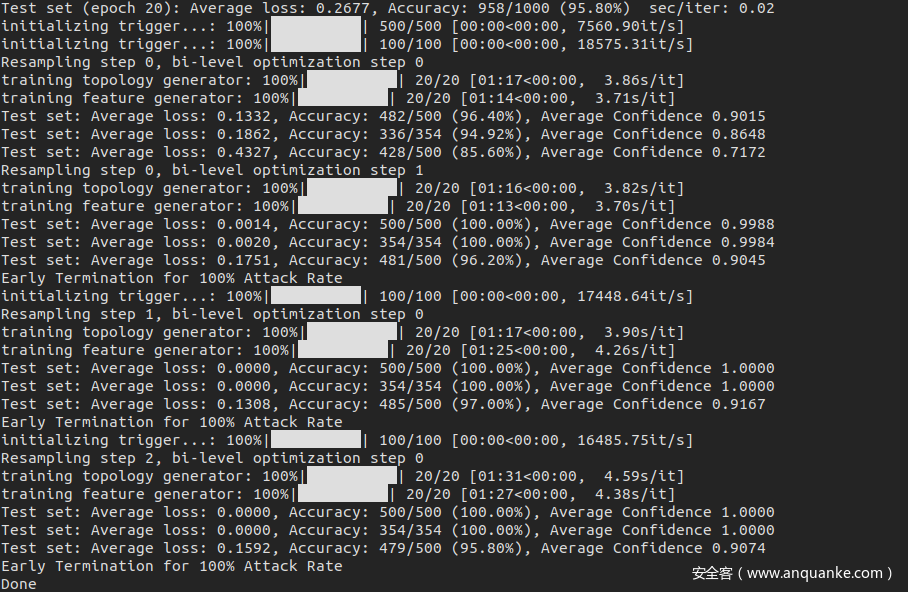
攻击代码运行后结果如下
可以看到攻击成功率达到了100%
参考
1.Xi Z, Pang R, Ji S, et al. Graph backdoor[C]//30th {USENIX} Security Symposium ({USENIX} Security 21). 2021.
3.Ryan A. Rossi and Nesreen K. Ahmed. The Network Data Repository with Interactive Graph Analytics and Visualization. 2015.


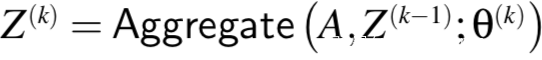
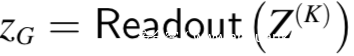
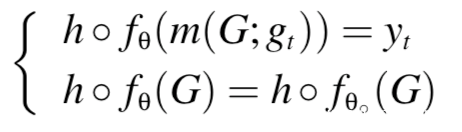
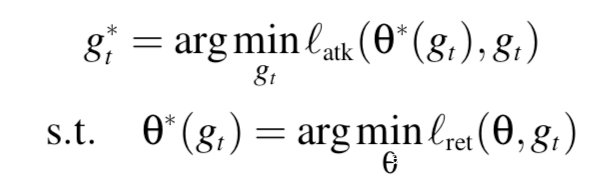
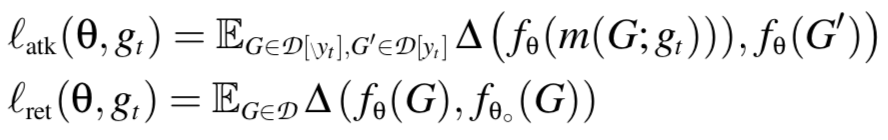
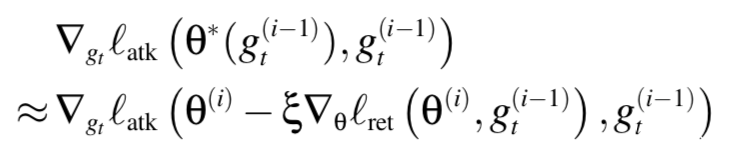
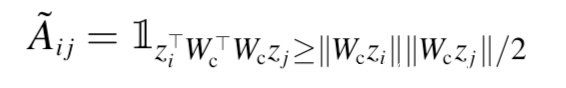
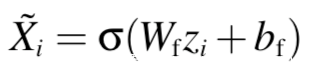








发表评论
您还未登录,请先登录。
登录