前言
可以发现RSA中的很多攻击方法都是从数论四大定理推导出的,所以找时间好好学习了一下数论四大定理的证明及其应用场景——Rabin算法。
欧拉定理
若n,a为正整数,且n,a互素,即gcd(a,n) = 1,则
a^φ(n) ≡ 1 (mod n)
证明
首先,我们需要知道欧拉定理是什么:
数论上的欧拉定理,指的是
aφ(n)≡1(mod n)
这个式子实在a和n互质的前提下成立的。
证明
首先,我们知道在1到n的数中,与n互质的一共有φ(n)个,所以我们把这φ(n)个数拿出来,放到设出的集合X中,即为x1,x2……xφ(n)
那么接下来,我们可以再设出一个集合为M,设M中的数为:
m1=a∗x1m2=a∗x2……mφ(n)=a∗xφ(n)
下面我们证明两个推理:
一、M中任意两个数都不模n同余。
反证法。
证明:假设M中存在两个数设为ma,mb模n同余。
即ma≡mb
移项得到:ma−mb=n∗k
再将m用x来表示得到:a∗xa−a∗xb=n∗ka∗xa−a∗xb=n∗k
提取公因式得到a∗(xa−xb)=n∗ka∗(xa−xb)=n∗k
我们现在已知a与n互质,那么式子就可以转化为:
xa−xb≡0(mod n)
因为a中没有与n的公因子(1除外)所以a mod n != 0 所有只能是 xa−xb≡0(mod n)。
又因为xa,xb都是小于n的并且不会相同,那么上述的式子自然全都不成立。
假设不成立。
证得:M中任意两个数都不模n同余。
二、M中的数除以n的余数全部与n互质。
证明:我们已知mi=a∗xi
又因为a与n互质,xi与n互质,所以可得mi与n互质。
带入到欧几里得算法中推一步就好了。
即:
gcd(a∗xi,n)=gcd(mi,n)=gcd(n,mi mod n)=1
证毕。
三、根据我们证得的两个性质,就可以开始推式子了。
首先,根据前两个推论可以知道,M中的数分别对应X中的每个数模n同余。
(即是双射关系:首先M中的数在模n下不同余,即不相同,然后有φ(n)个m;其次有φ(n)个不相同的x与n互质,所以m与x是双射关系)
所以可以得到:
m1∗m2∗……∗mφ(n)≡x1∗x2∗……∗xφ(n)(mod n)
现在我们把替换成x的形式,就可以得到:
a∗x1∗a∗x2∗……∗a∗xφ(n)≡x1∗x2∗……∗xφ(n)(mod n)
aφ(n)∗(x1∗x2……∗xφ(n))≡x1∗x2……∗xφ(n)(mod n)
(aφ(n)−1)∗(x1∗x2……∗xφ(n))≡0(mod n)
然后,由于(x1∗x2……∗xφ(n))!≡0(mod n)
所以 (aφ(n)−1)≡0(mod n)
所以 aφ(n)≡1(mod n)
应用:RSA的解密
欧拉定理在RSA中可用于证明 M=Cd mod N :
费马小定理(欧拉定理特殊型情况)
对于质数p,任意整数a,均满足:ap-1≡1(mod p)
那么,ap-2就是a在模p下的逆元了~
孙子定理(中国剩余定理 CRT)
设正整数两两互素,则同余方程组
有整数解。并且在模下的解是唯一的,解为
其中,而
为
模
的逆元。
证明
具体证明如下:
例:找出所有整数x,使其被3,5和7除时,余数分别为2,3和2
x≡2(mod 3)
x≡3(mod 5)
x≡2(mod 7)
=> x = △ + 357*t (△为期中的一个解,t为整数)
在同余中最重要的观念就是求出第一个解,那么x = △ + 357*t就是通解。那怎么求一个解呢?
利用同余的加性:
把x拆成a+b+c,即x = a + b + c
令
a≡2(mod 3)
a≡0(mod 5)
a≡0(mod 7)
=>a=35p(可以看到p取1的时候满足a≡2(mod3),即a=35)
为何这样取?从接下来的取法可知:b 和 c 都会取 3 的倍数,这样子就能保证,x mod 3 = 2,我们标记这样的取法为FLAG
接下来要求b:
b≡0(mod 3)
b≡3(mod 5)
b≡0(mod 7)
=>b=21q(可以看到q取3的时候满足b≡3(mod5),即b=63)
求c
c≡0(mod 3)
c≡0(mod 5)
c≡2(mod 7)
=>c=15m(可以看到m取2的时候满足c≡2(mod7),即c=30)
得
x≡2(mod 3) ≡ a + b + c
x≡3(mod 5) ≡ a + b + c
x≡2(mod 7) ≡ a + b + c
a b c 都求出来之后,可以利用同余的加性
x = a + b + c = 128是一个解,x = 128 + 105t 在适当调整t之后就可以求出x在任何范围内的解,比如说求最小正整数解,这时候t取-1,得x=23
利用同余的乘性:
之前令x = a + b + c,用同余的乘性之后x = 2a’ + 3b’ + 2c’ (此时令a’=b’=c’=1,就相当于同余的加性了)
a’≡1(mod 3)
a’≡0(mod 5)
a’≡0(mod 7)
=>a’=35p(可以看到p取2的时候满足a’≡1(mod3),即a’=70)
接下来要求b’:
b’≡0(mod 3)
b’≡1(mod 5)
b’≡0(mod 7)
=>b’=21q(可以看到q取1的时候满足b’≡1(mod5),即b’=21)
现在来看c’
c’≡0(mod 3)
c’≡0(mod 5)
c’≡1(mod 7)
=>c’=15m(可以看到m取1的时候满足c’≡1(mod7),即c’=15)
有了a’ b’ c’之后就可以得到 x = 2a’ + 3b’ + 2*c’
代入a’ b’ c’之后就可以得到x的一个解及其通解
x = 2*70 + 3*21 +2*15
x = 233 + 105t
在知道同余的加性和乘性之后再看下面这个公式就没有什么问题了
其中,ai就是题目所要求的剩余,M1就是前文提到的标记取法FLAG,而M1-1就是在同余的乘法性中为了满足a1‘≡1 mod (mi)
威尔逊定理
当且仅当p为素数时有,
(p−1) ! ≡ −1(mod p)
证明:
首先:
p−1 ≡ −1(mod p)
那么我们只需要证明 (p−2)!≡1(mod p)
也就是说,除去 1 后,如果 2,3,…,p−2 能够两两配对,且每对数乘积模 p 后为 1 的话,威尔逊定理就成立了,然后我们考虑这其实就是对于 2,3,…,p−2去找 模 p 意义下的逆元。
然后考虑一下二次剩余里面的衍生知识,我们可以知道对于 x2≡1(mod q)只有两个解(1,p-1),而这两个数已经被我们安排掉了,也就是说 2,3,…,p−2中不存在某个数的逆元是自己本身。
然后 集合 A={1,2,3,…p -1}; 构成模p乘法的缩系,即任意i∈A ,存在j∈A,使得: ( i,j ) ≡ 1 ( mod p )
也就是说,除去1和p-1外,其余的两两配对互为逆元
证毕
应用:Rabin算法
在解Rabin算法前,我们需要一些定理、推论
定理1
欧拉判别定理, c是模p的平方剩余的充要条件是 ,(c1/2)φ(n) ≡ 1(mod P)
证明:
首先,由于是一个奇素数,由费马小定理,
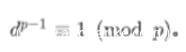
是一个偶数,所以有
是一个素数,所以
和
中必有一个是
的倍数。因此
模
的余数必然是1或-1。
• 证明若是模
二次剩余,则
若是模
二次剩余,则存在
,
跟
和
互质。根据费马小定理得:
• 证明若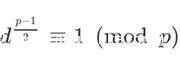
是模
的二次剩余
是一个奇素数,所以关于
的原根存在。设
是
的一个原根,则存在
使得
。于是
是
的一个原根,因此
模
的指数是
,于是
整除
。这说明
是一个偶数。令
,就有
。
是模
的二次剩余
定理2
二次同余式x2 ≡ c (mod p)的解为:
x ≡ ±c(p+1)/4 (mod p)
证明
由于p是素数,显然a与p互素,再由欧拉判别定理, a是模p的平方剩余的充要条件是 ,
(c1/2)φ(n) ≡ 1(mod P)
即(c1/2)p-1 ≡ 1(mod p)
带入原式,得x2 ≡ c·(c1/2)p-1 ≡ c(p+1)/2 ≡ (c(p+1)/4)2
则
x ≡ ±c(p+1)/4 (mod p)
定理3
如果整数c满足:
1) c为p的平方剩余
2) c为q的平方剩余
则: c为p*q的平方剩余,解x为:x ≡ ±(c(p+1)/4(mod p))·(q-1(mod p))*q ± (c(q+1)/4(mod q))*(p-1(mod q))·p (mod p*q)
证明
二次同余式: x2 ≡ c (mod pq)
等价于同余式组 : x2 ≡ c (mod p) ①
x2 ≡ c (mod q) ②
由定理2
①式解为 x ≡ ±c(p+1)/4 (mod p)
②式解为 x ≡ ±c(q+1)/4 (mod q)
由CRT,解为 x ≡ ±(c(p+1)/4(mod p))·(q-1(mod p))*q ± (c(q+1)/4(mod q))*(p-1(mod q))·p (mod p*q)
Rabin加密
选择两个大素数p和q做为私钥
计算n = p * q做为公钥
若明文为m,则密文为c ≡ m^2 (mod n)
Rabin解密
我们首先计算出x1和x2,使得
x12 ≡ c (mod p),①
x22 ≡ c (mod q),②
i)p和q都是模4余3的数
由于p是素数,显然c与p互素,再由定理2
得
x1 ≡ ±c(p+1)/4 (mod p)
x2 ≡ ±c(q+1)/4 (mod q)
(一正一负,负的计算可简化为 模–正,如:-x1 ≡ p – x1 (mod p))
从这里可以看出来如果p和q不是模4余3的话,c的指数就不是一个整数,也就不能用这个方法计算了
接着我们求出p在模q下的逆,设为a,即ap ≡ 1 (mod q)
然后我们求出q在模p下的逆,设为b,即bq ≡ 1 (mod p)
求出来a,b用于中国剩余定理
带入x ≡ ±(c(p+1)/4(mod p))·(q-1(mod p))*q ±(c(q+1)/4(mod q))*(p-1(mod q))·p (mod p*q)
得 x ≡ ±(c(p+1)/4(mod p))·b*q ±(c(q+1)/4(mod q))*a·p (mod n)
设c(p+1)/4(mod p) 为cp,c(q+1)/4 (mod q)为cq
其中有一个为我们想要的明文m。
exp:
import gmpy2
def n2s(x):
return hex(x)[2:].decode("hex")
c =
p =
q =
n = p*q
c_p = pow(c,(p+1)/4,p)
c_q = pow(c,(q+1)/4,q)
a = gmpy2.invert(p,q)
b = gmpy2.invert(q,p)
x = (b*q*c_p+a*p*c_q)%n
y = (b*q*c_p-a*p*c_q)%n
print n2s(x)
print n2s(n-x)
print n2s(y)
print n2s(n-y)ii)p和q不是模4余3的数
这里涉及 Cipolla’s algorithm ,先知已经有一篇讲的不错的文章了 https://xz.aliyun.com/t/5113#toc-4
题目实例
UNCTF – 一句话加密
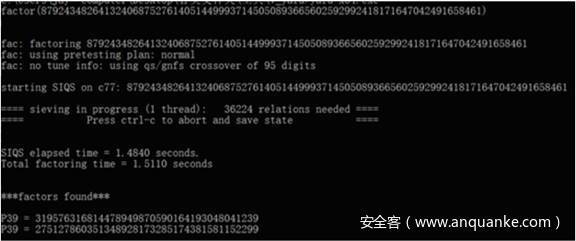
题目是给了一张图,隐写了一个模n
n = 0xc2636ae5c3d8e43ffb97ab09028f1aac6c0bf6cd3d70ebca281bffe97fbe30dd
可以发现n不大,直接用yafu分解可得
但是找不到e,最后试了试rabin,成功破解
exp用上面的那个就可~
roarctf – babyrsa
import sympy
import random
def myGetPrime():
A= getPrime(513)
print(A)
B=A-random.randint(1e3,1e5)
print(B)
return sympy.nextPrime((B!)%A)
p=myGetPrime()
#A1=
#B1=
q=myGetPrime()
#A2=
#B2=
r=myGetPrime()
n=p*q*r
#n=
c=pow(flag,e,n)
#e=0x1001
#c=
#so,what is the flag?加密中的(B!)%A的 ! 在这里是阶乘的意思,所以显然这里要用到威尔逊定理,不然这么大的一个数的阶乘,根本吃不消好吧
根据加密逻辑,这里是一个三素数系统,所以φ(n) = (p-1)(q-1)(r-1),然后r肯定是要通过先求出p,q来得出
然后关于p和q,题目给的信息都一样,所以求p和求q的解法肯定是一样的,
所以题目简化为,根据A1,B1解p
而p = (B!)%A (B是一个比A小的数)
虽然A,B均已给出且互素,但显然大数B的阶乘是不可能直接求得的,
所以要用威尔逊定理简化计算
简化过程如下:
已知 B! ≡ P(MOD A)
由于A是素数,所以有: (A-1)! ≡ -1 (MOD A)
即(A-1)(A-2)……(B+1)B! ≡ -1 (MOD A)
根据已知(A-1)(A-2)……(B+1)P ≡ -1 (MOD A)
变形为(A-2)……(B+1)P ≡ 1 (MOD A)
所以p即为(A-2)(A-3)……(B+1) 在模A 下的逆
exp
from gmpy2 import *
import sympy
A1=
B1=
A2=
B2=
n=
e=0x1001
c=
a = 1
for i in range(A1-2,B1,-1):
a = a*i % A1
b = 1
for i in range(A2-2,B2,-1):
b = b*i % A2
p = sympy.nextprime(invert(a,A1))
q = sympy.nextprime(invert(b,A2))
r=n/p/q
phi = (p-1)*(q-1)*(r-1)
d = invert(e,phi)
m=pow(c,d,n)
print hex(m)[2:].decode('hex')HECTF – easy_rsa
from gmpy2 import *
from Crypto.Util import number
#e = have a try~
p = number.getPrime(1024)
q = number.getPrime(1024)
nothing = 251560377963038761190200797029988859033 # getPrime(128)
n = p*q
fn = (p-1)*(q-1)
d =inverse(e, fn)
something=(p-1)d+nothing
enc = pow(flag, e, p*q)
#n=
#something=
#enc=题目给了,nothing(下面记为r),something(下面记为s),其中 (p-1)d= s – r
目的很明确,就是分解大数n
这一题的思路就是利用GCD来约出n的因子
所以首先要获得一个p的倍数
根据费马小定理
2p-1 ≡ 1 (mod p ) 显然成立 (主要是为了利用题目中给出的(p-1)d)
所以设A = 2p-1 – 1 = kp
然后利用欧拉定理,我们直接利用上文中提到的RSA的解密证明中的结论
(2p-1)ed ≡ (2p-1) (mod n)
由题,(p-1)d = s – r
所以A ≡ 2p-1 – 1 ≡ (2p-1)ed – 1 ≡ 2es-er – 1 (mod n)
所以 gcd( 2es-er – 1 , n)
即 gcd(kp , pq)
即可得到 p
exp:
import libnum
from gmpy2 import *
import sympy
enc=
n=
something=
nothing=
e=1
while(True):
try:
e=sympy.nextprime(e)
a=pow(2,e*something-e*nothing,n)-1
p=libnum.gcd(a,n)
q=n/p
fn=(p-1)*(q-1)
d=invert(e,fn)
flag=libnum.n2s(pow(enc,d,n))
if "hebtu" in flag:
print flag
break
except:
continue构造GCD
可以看出,构造gcd来求大数n的因子以此来分解n是一种很好又很巧妙的方式,来看这一题
from Crypto.Util.number import getPrime, isPrime, getRandomNBitInteger
p = getPrime(512)
q = getPrime(512)
n=p*q
a=int(pow((q+p),2019,n))
b=int(pow(p+2019,q,n))
n=
a=
b=这里,我们要通过已给出的a和b,来分解n
通过a,b和p,q的关系,我们要想办法用a,b凑出一个GCD来求出n的一个因子
解题过程如下:
由 a ≡ (p+q)2019 (mod n)
可得 a ≡ (p+q)2019 ≡ p2019 (mod q) 【二项式展开定理】
由 b ≡ (p+2019)q (mod n)
可得 b ≡ (p+2019)q ≡ p+2019 (mod q) 【费马小定理:(p+2019)q-1 ≡ 1 (mod q)】
所以 a ≡ (b – 2019)2019 (mod q)
即 a = (b – 2019)2019 + kq
这样我们就可以凑出一个GCD
GCD( (b – 2019)2019-a,n)= GCD( Kq,n)= q
解题完毕
总结
这一次学习了数论四大定理的证明、应用,以及rabin密码的解法。发现其实很多解法、攻击方法都是多种定理的结合运用,有时候还要引出各种推论,很灵活~
参考
欧拉定理证明: https://www.cnblogs.com/wangxiaodai/p/9758242.html
中国剩余定理证明: https://blog.csdn.net/Rain722/article/details/53230707
威尔逊定理证明: https://www.cnblogs.com/Judge/p/10755703.html
Rabin算法: https://veritas501.space/2017/03/01/%E5%AF%86%E7%A0%81%E5%AD%A6%E7%AC%94%E8%AE%B0/
https://en.wikipedia.org/wiki/Rabin_cryptosystem
https://blog.csdn.net/qq_24451605/article/details/45093911
最后感谢Lur大佬的一手指点~



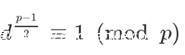
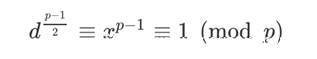
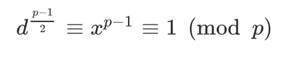








发表评论
您还未登录,请先登录。
登录