前言:
在NCTF上遇到了一道出题人用来压轴的RSA,与正常RSA加密不同的是,本题的e是φ(p)和φ(q)的一个因子。在出题人给出hint后,我找到了一篇paper,侥幸用paper中提到的算法拿到了一血~
该算法可以在有限域Fq中开r次根,但需要s,满足r^s整除q-1,即r^s | q-1,并且s要小。
On r-th Root Extraction Algorithm in Fq
paper: https://eprint.iacr.org/2013/117.pdf
引言:
我们让r为一个大于1的整数,那么有现存的两种算法用来在有限域Fq中开r^s次根, the Adleman-Manders-Miller algorithm 和 the Cipolla-Lehmer algorithms
假设r<<log q ,由于 the Adleman-Manders-Miller algorithm 要求s满足 r^s | q-1 并且 r^(s+1) 不能整除 q-1,所以它的时间复杂度O(logrlog4 q) 比 the Cipolla-Lehmer algorithms 的时间复杂度O(rlog3 q) 要高。但是,由于Cipolla Lehmer需要繁琐的扩展字段算法,当s比较小时,the Adleman-Manders-Miller algorithm 要比之更为有效。
另一方面,在某些情况下还存在比 Tonelli-Shanks 计算更快的其他方法来做开方运算。例子就是当 q ≡ 3 (mod 4).
当c时Fq中的二次剩余时,c的其中一个根就是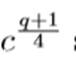
当s=2,3时,也有类似的方法, Atkin , Mu¨ller and Kong et al ,他们的方法在这种情况下, 要比Tonelli-Shanks and the Cipolla-Lehmer 表现得更为出色。
但是作者认为这些方法不能很好的解决普遍的情况,所以作者展示了一种,新的开根的方法,只用一个预计算好的基元,一次指数运算,并且在s很小的时候十分高效。
开二次根算法:
有一些高效的公式,分别当 q ≡ 5 (mod 8) ,或者 q ≡ 9 (mod 16) 。如果q ≡ 5 (mod 8) ,属于 q ≡ 1 (mod 4), 的一种特殊情况, Atkin 有一种只进行一次指数运算的高效的公式。
Algorithm 1 Atkin’s algorithm when q ≡ 5 (mod 8)
方程,x^2 = a mod (q),已知a,求x
Algorithm 2 Mu¨ller’s algorithm when q ≡ 9 (mod 16)
方程,x^2 = a mod (q),已知a,求x
其中第二步有个神奇的东西 η(d) ,paper中给的定义是
,然鹅想不出怎么让它等于-b,(还求大师傅们指点~)
在有限域中 Fq 开 r^s 根 [ q ≡ lr^s + 1 (mod r^(s+1)) ]
首先我们需要一个质数q,并且有一个r,满足 r | (q-1),(如果r与q-1互质,那问题就很简单了,r的逆用欧拓很快就能找到)然后会存在一个s,s是满足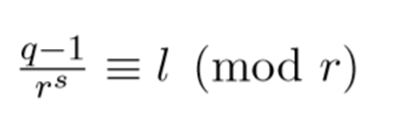
即会满足
定理1:在域Fq中,给定一个r次幂c,存在一个b,使得c^(r-1)·b^r 具有r^t阶,(t<s)
证明:
我们设一个l,满足gcd(l,r)=1,那么存在β (0≤β<l),满足 rβ+r−1 ≡ 0 (mod l) 即存在α,满足 rβ + r−1 = lα.
然后,我们设一个 ζ 为,
则有
其中,
因为c是域Fq中的r次幂,故ζ拥有r^t阶,(0≤t<s) (为啥这里t就小于s了,求指点~)
利用:
在域Fq中,我们令 ξ 为 一个r^2阶本原单位根,ξ可以通过公式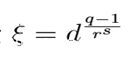
由此,我们设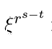
因为
所以我们有
由此我们将展现一个新的定理,在合适的情况下,我们用一次指数运算可以找到r次剩余的一个r次根,
定理2:定义u ≡ j·(r^t −1)·r^(s−t−1 ) ≡−jr^(s−t−1) (mod r^(s−1)). 那么在域Fq中c的一个r次根为 cbξ^u ,其中b在定理1中给出。
证明:
(由于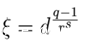
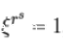
证毕。
注1: rβ + r −1 = lα 即 r(β + l) + r −1 = l(α + r)。这说明,α (mod r )是确定的,β(mod l)是确定的,所以对于任意的α 满足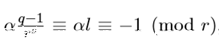
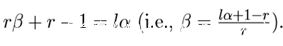
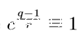
注2:cb的值可以化成
其中α是一个整数(0<α<r),满足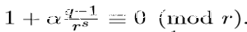
注3:对于 ij ≡ 1 (mod r^t) ,当r^t很大(t>1 并且在r^t阶循环群中的离散对数很难处理)时,其中的i和j找起来是比较困难的,所以这个方法适合在r和t都比较小的时候,也可以被视作是另一个版本的Adleman-Manders-Miller algorithm。
举例与算法
终于到实例环节了~
例1 q ≡ lr + 1 (mod r^2) 0 < l < r:
在这种情况下,s=1,所以t=u=0,所以r次根c可以表示为cbξ^u = cb = 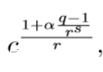
当r = 2,s=1就意味着, q ≡ 3 (mod 4) ,α在这里可以算出是1,带入公式,c的一个二次根就是众所周知的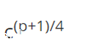
当r = 3,s=1 就意味着 q ≡ 4 (mod 9) 或者 q ≡ 7 (mod 9) ,先算出α,然后带入公式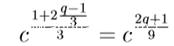
或是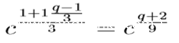
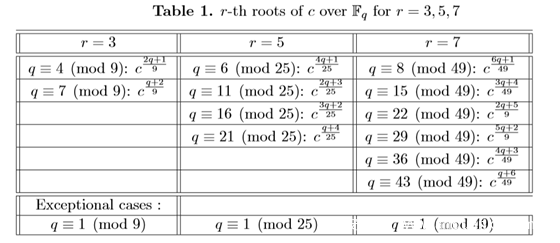
这里有个表
最底下一样有例外,此时也就以为着r=0,r=0.还有啥根可开~
可见,当s=1时,在 q ≡ 1 (mod r) 并且 q !≡ 1 (mod r^2) 时,即q的(r-1) 种情况都可以借该公式进行一次指数运算就可开根,得到一个解。(推理过程一知半解的,但是结论用起来是真的香)
例2 q ≡ lr^2 + 1 (mod r^3) 0 < l < r:
当s=2.那么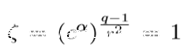
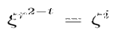
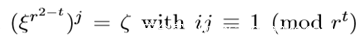
因此,r次根可以表示为 cbξ^u ,具体的值上文已给,当t=0,u=0,x=cb是一个r次根,当t=1,u ≡−j (mod r) ,x= cbξ^−j是一个r次根。(所以我们还是希望t=0,这样计算就会极其方便~)
Algorithm 3 Our cube root algorithm when q ≡ 1 (mod 9) and q ̸≡ 1 (mod 27)
x^3=c (mod q) ( (q = 9l + 1 (mod 27) with l = 1,2, i.e., q ≡ 10,19 (mod 27)) )
解读一下:
,其中d在域Fq种不是一个r次幂(遍历一下,随便取一个就好)。
ζ=c^r−1·b^r = c^2·b^3=X^2b
如果,ζ=1,则说明t=0,那么x=cb=X
如果,ζ=B=ξ^r,那么t=j=1,x=cbξ^-j=cbξ^2=XA^2
否则,j=2,x=cbξ^-j=cbξ^-2=XA
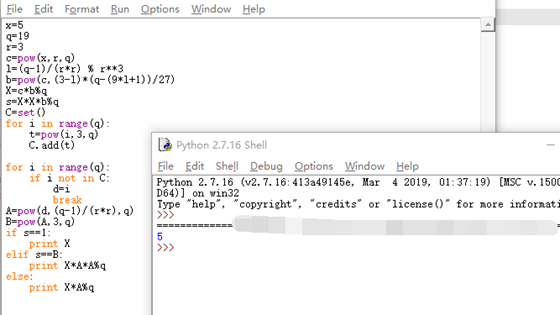
验证:
成功~
以下同
Algorithm 4 Our 5-th root algorithm when q ≡ 1 (mod 25) and q ̸≡ 1 (mod 125)
x^5=c (mod q) (q = 25l + 1 (mod 125) with l = 1,2,3,4, i.e., q ≡ 26,51,76,101 (mod 125))
例3 q ≡ lr^3 + 1 (mod r^4) 0 < l < r:
当s=3,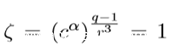
所以,c的r次根可以表示为cbξ^u,当t=0,u=0,x=cb即是c的一个r次根,当t=1,
u ≡ −jr (mod r^2), 当t=2, u ≡ −j (mod r^2),
计算过程类比上文,只是要考虑的(u)的情况增加到了r^2种。
实战
回到开头说的NCTF crypto全场两解(大佬都去隔壁打D^3了~)的压轴——easyrsa
题目:(数字太大,就省去了)
from rsav import *
e = 0x1337
p =
q =
n = p * q
'''
assert(flag.startswith('NCTF'))
m = int.from_bytes(flag.encode(), 'big')
assert(m.bit_length() > 1337)
c = pow(m, e, n)
print(c)'''
c= 解题思路:
很普通的加密手段,然后p,q都给了,其中,e|q-1;e|p-1
唯一难点就在e是φ(n)的一个因子所以根本无法求出私钥d
第一步是类似rabin,先将m^e ≡ c (mod n)分解成同余式组
m^e ≡ c (mod p)
m^e ≡ c (mod q)
求出m1和m2,再用CRT就好了
至于m的求解,本题的条件正好符合上文的例1,
于是我们先遍历出α,然后就可以求得m1了,
再算出另一个α,得到m2,然后CRT走一波,就可以出明文的一种情况了,
然而一共有e^2种情况
当e=2,rabin解密,有e^2种情况,因为同余方程组里的每一个方程都有两种情况。
当e=3,每个就有三种,CRT后一共就有3^2种
根据hint2,里面有提供当找到一种解后找到其余解的算法
原理在这 https://crypto.stackexchange.com/questions/63614/finding-the-n-th-root-of-unity-in-a-finite-field
在有限域Fq中,乘法子群的阶为q-1,如果n不满足n|q-1,那么n次单位根只有1本身,如果n满足n|q-1,那么就有n个单位根。
由费马小定理
所以我们有n次单位根
当我们这个n次单位根不等于1时,我们就可以利用它和我们找到的一个根来生成一个阶为n的循环群,这个群里所有的元素即为我们想要的所有的根。
这样我们构造exp,遍历这0x1337*0x1337=24196561种可能,就能解出真正的密文了
import gmpy2
def n2s(x):
try:
try:
flag = hex(x)[2:].decode("hex")
except:
flag = hex(x)[2:-1].decode("hex")
except:
flag=''
return flag
def onemod(p,r):
t=p-2
while pow(t,(p-1)/r,p)==1: t-=1
return pow(t,(p-1)/r,p)
def solution(p,root):
g=onemod(p,0x1337)
may=[]
for i in range(0x1337):
may.append(root*pow(g,i,p)%p)
return may
c =
p =
q =
e = 0x1337
n = p*q
c_p = pow(c,(1+3307*(p-1)/e)/e,p) #p对应的α=3307
print "find one"
C1=solution(p,c_p)[::-1] #逆序,问题不大,只是跑过一次,发现答案在两千多万次后
print "find all"
c_q = pow(c,(1+(2649*(q-1)/e))/e,q) #q对应的α=2649
print "find another"
C2=solution(q,c_q)[::-1]
print "find all"
a= gmpy2.invert(p,q)
b = gmpy2.invert(q,p)
#x = (b*q*c_p+a*p*c_q)%n
flag=0
for i in C1:
for j in C2:
flag+=1
if flag%1000000 == 0:
print flag
x = (b*q*i+a*p*j)%n
if "NCTF" in n2s(x):
print n2s(x)
exit(0)
总结
这一次借NCTF了解了在域中开根的一种高效方法,这种方法似乎比出题人soreatu师傅的预期解还要高效~
并且有幸拿到了一个一血,不得不说,这公式,真香~
另外感谢这次NCTF,在这次密码学的赛题中学到了很多,另外一道childrsa也很有意思(有意思在我意外的发现了其中一个神奇规律23333)
最后再次感谢soreatu师傅制作的优质赛题以及赛后详细的wp与指点~



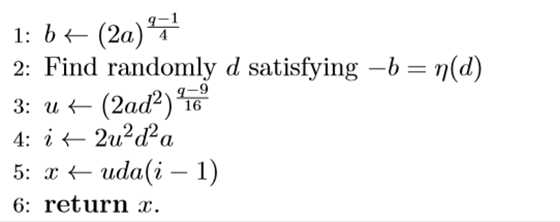

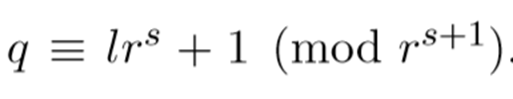
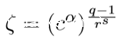
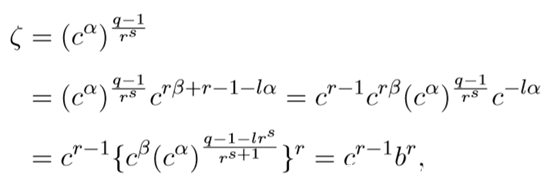
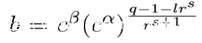
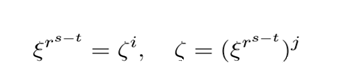
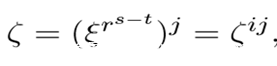
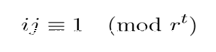
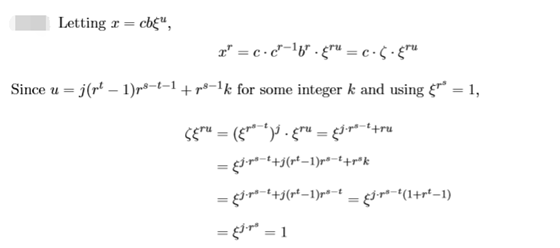
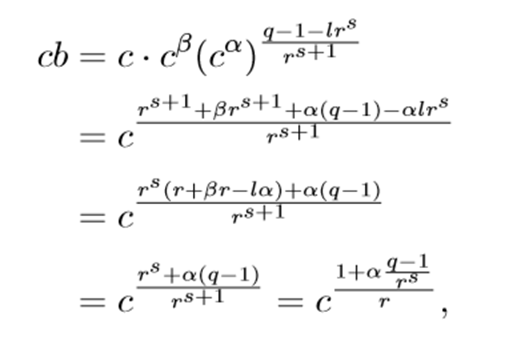
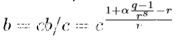
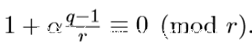
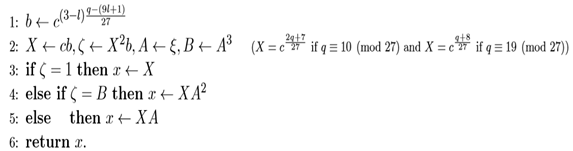
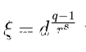
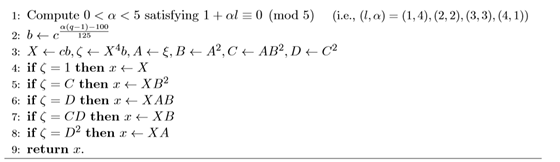
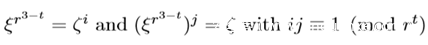


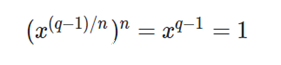
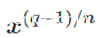








发表评论
您还未登录,请先登录。
登录