这一块咕咕咕了好久,暑假了,终于才有时间去细究coppersmith背后的原理。
前言
还记得自己刚入门CTF后打的第一个相对比较大的比赛就是2019届的强网杯,那个时候密码学就有一道copperstudy的题目。对于刚入门时来说,觉得那道题简直就是(无法形容)。后来才知道原来里面的每一关都可以在github上找到相应的脚本。但是当我想去找原理的时候,却发现,,,找不到。所以也才有了这篇文章。
Coppersmith’s Method
首先看看Coppersmith’s Method这玩意儿能干啥。简而言之,就是有一个函数,比如F(x) = x^3+x+123,然后有一个模数,比如 M = 77,然后假设存在一个x0 满足F(x0) ≡ 0 (mod M), 并且如果这个x0小于某个特定的值,那么就可以用Coppersmith’s Method去找到这个x0。【PS:想要实现这个手法还是需要掌握一点格基规约的相关知识的(至少知道格基规约是干啥的,结果输出的是啥)】
总的来说,如果能将M分解,那么找到这个x0是容易的,用一个中国剩余定理即可;否则就是困难的。对应的,如果我们能够找到一个解满足x^2 ≡ 1 (mod M) 并且这个x不等于±1 (mod M),那么我们用一个GCD就能将这个M给分解。具体可参看二十年以来对 RSA 密码系统攻击综述一文。因此,我们并不希冀于有一个有效的算法对于所有这样的同余式都能找到解,否则也就意味着大数分解问题破解了。
既然不能对所有的同余式都能找到解,那能找到解的条件是啥呢?对于度为d的多项式F(x),如果x0满足F(x0) ≡ 0 (mod M) 并且|x0|< M^{1/d-ε},那么这个解x0就能在多项式时间内被找到。
First Steps to Coppersmith’s Method
首先我们有在模M下的度为d的并且系数为整数的一个首一多项式:
【如果多项式不是首一的,我们整体的系数乘上一个a{d}(x^d的系数)在模M下的逆元即可,如果a{d}在模M没有逆元,那这条同余式可以拆成同余式组,但这并不是这篇文章讨论的重点】假设我们知道存在一个整数x_0满足F(x0) ≡ 0(mod M ) 并且 |x0|<M^{1/d},我们的任务就是找到这样的x0。我们想,如果有这样一条多项式G(x),他的解也是x0。但是他的系数很小,导致x0可以满足G(x0)= 0【注意这里是等号,不是同于号】Coppersmith’s Method就是想办法去将这个F(x)变形为成为这样的G(x)。
example 1
假设M=17 * 19=323,F(x)=x^2+33x+215,我们想找到一个小根x0满足F(x0)≡ 0 (mod M)【这里的x0=3,但是在整数域下,F(3)!=0 】
我们可以找到一个多项式G(x) = 9 * F(x) – M * (x+6) = 9x^2 – 26x-3 满足G(3)=0,这个解可以直接用求根公式得到,如果次数比较大,也可以用牛顿迭代法。
好了,这就是一元Coppersmith’s Method核心思路了,其实一点也不难的吼。
接下来主要是对这个x0的界的一些讨论以及如何尽量的提高这个界的一些手法。
我们定义X为这个|x0|取值的上界,
然后我们将F(x)表示为一个行向量b=(a0, a1X, a2X^2 ,…, adX^d)
Theorem 1(Howgrave-Graham)
首先我们有F(x), X, M, b这几个上面提到的值
也有F(x0) ≡ 0 (mod M)
那么,当||b_F||<M/sqrt{d+1},则有F(x0) = 0
proof
【这里不等式的第三个就用到了柯西不等式的性质】
这个定理对于确定x0的边界值$X$很重要。
之前我们找到的G(x)我们直接给出的,现在开始说这个$G(x)$该怎么去找,首先我们考虑度d条 多项式 Gi(x) = Mx^i(0 ≤i< d) ,还有一个 F(x),显然,这里一共d+1条式子,他们的均有解 x = x0 (mod M) ,我们将他们的系数向量组合成一个矩阵
X为x0的取值上界
显然,这个矩阵的行列式为det(L)=M^d * X^ {d(d+1)/2}
然后我们利用LLL算法做一个格基规约,然后设规约后的矩阵的第一行行向量为b’,
这一点需要用到LLL的一个性质就是,
至此,我们初步的有了一个X的取值范围,但这还并未达到M^{1/d-ε}的程度。。。
example 2
设M=10001,多项式F(x)=x^3 + 10x^2 + 5000x – 222,【这里其实我们已经提前知道x0 = 4,所以满足x0 < M^{1/6}】
这里我们可以计算x0的大致上界为X=10,所以我们构造格
利用LLL规约后我们可以得到第一行(the first row)为(444,10,-2000,-2000),所以我们找到多项式G(x)=444 + x – 20x^2 – 2x^3,最后再来个牛顿迭代法求根可得x0=4
【PS:由于平台无法显示公式,所以为了美观和方便,有一部分我直接采取了截图的方式】


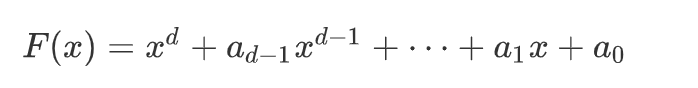

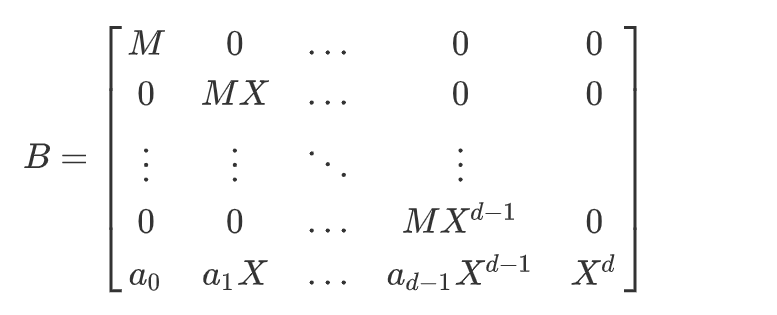
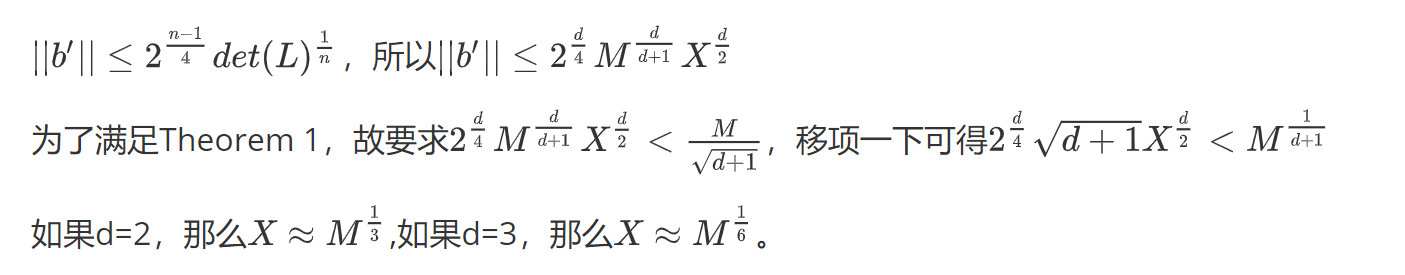








发表评论
您还未登录,请先登录。
登录