硬件安全系列 第二篇 逻辑电路基础知识介绍（二）

 

前言

第二部分 逻辑表示方式以及处理算法

 

Boolean Representation via BDDs and SAT

BDD Binary Decision Diagrams

BDD是什么。Binary Decision Diagrams 二进制决策图

二进制决策图是表示和操作布尔逻辑的最通用和有用的数据结构之一。

那么二进制决策图长什么样呢。

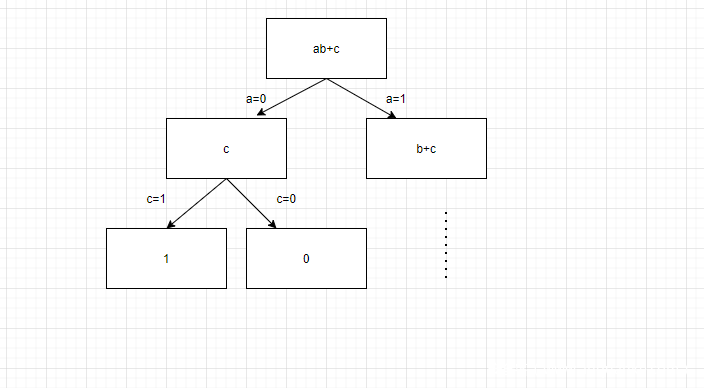
如图所示，就是树状图，每一个分支对应一个输入的确定，从而确定输出，这也表示了所有状态下输入和输出的对应关系。但是呢，这样的表示方法在输入增加时，树状图成指数增长，所以我们显然需要一些方法来简化。

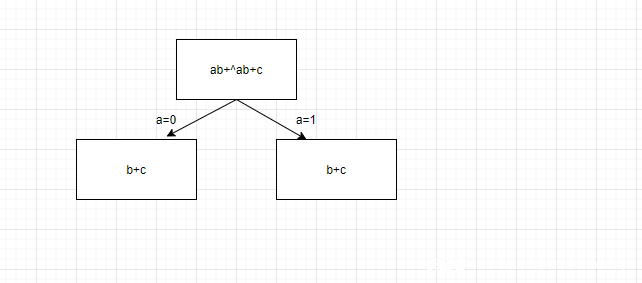
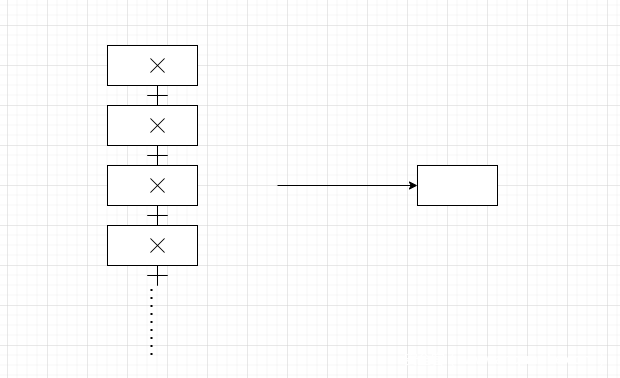
忽略节点：当某一情况下的某一输入对结果不发生影响时，我们忽略这一输入对应的两个分支。如图所示

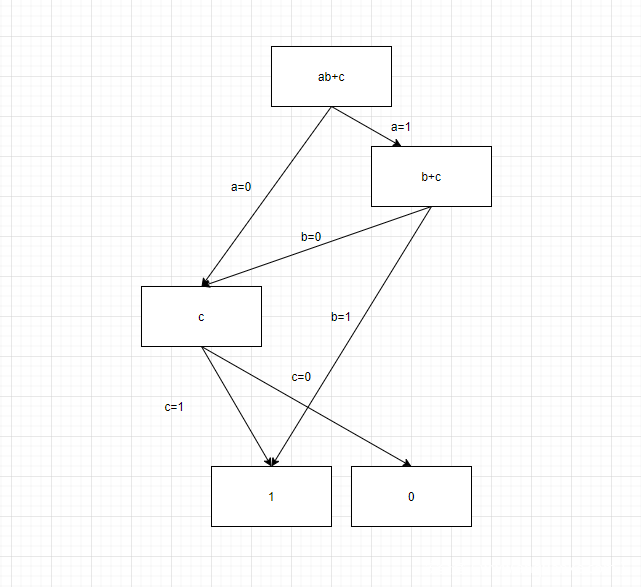
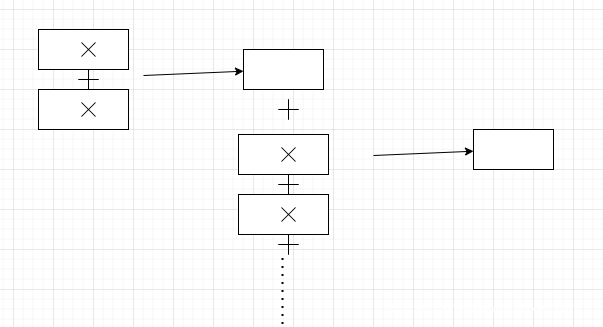
共用节点：共用节点存在两种类型。第一种是由于输出一定是0或者1，我们只需要将所有分支的最终输出指向0或者1，就可以减少输出的分支。第二种是对于多个输入输出对应关系，在经过一些0/1简化后，可能存在相同状况，即从某一分支开始，之后的部分逻辑关系完全一致，我们将这一部分逻辑关系用同一个树状图表示，仅仅是前置的输入指向不同。又或者是不同对应关系在最初的部分逻辑关系中存在相同情况，我们同样可以将这一部分逻辑关系用同一个树状图表示，仅仅是输出指向不同节点。

接下来的图片分别对应第一种类型和第二种类型的两种情况

除此之外，输入判断的先后会对整个树状图的大小有极其重要的影响。

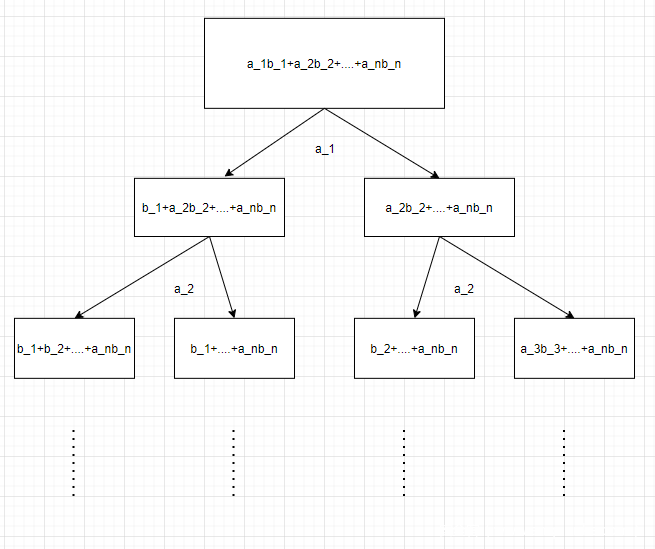
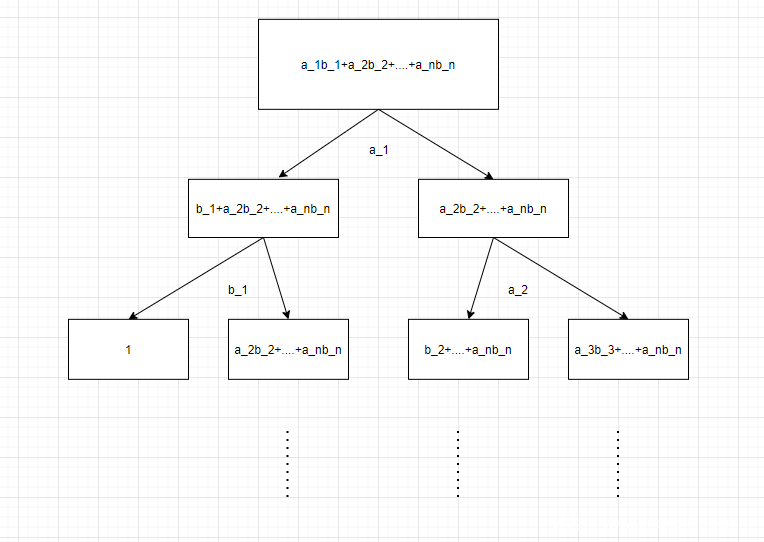
如图所示，当我们先判断a_1,a_2,a_3…..，然后判断b_1,b_2,b_3….我们会发现，一直判断到b_1才会出现第一个可能的输出，然而在n次判断后，这一次判断的分支会存在2^（n+1），毫无疑问，这是一个巨大的工程量。而当我们先判断a_1b_1时，无疑会减少一个巨大的分支。

SAT satisfiability

对于一个逻辑关系，我们往往需要的是该逻辑关系成立，比如network repair中z = ! (F xor G)，我们特意在最后结尾添加非运算，使得真才是我们期待的结果。这既符合现实逻辑上的关系，又符合电子逻辑关系。

所以，对一个系统来说，有时候我们并不期望得到所有的结果，只需要知道这件事情在某种条件下能够成立，我们去尽力满足这个条件即可。因此，SAT被提了出来。

在一个概念被提出之后，我们需要做的就是找到一个方法实现这个概念。首先我们提出一个表达方式CNF Conjunctive Normal Form，连接的一般方式。其形式是XXX+XXXX+XXXX，语言描述就是多个命题的和。

为什么选择和的形式呢。

因为or逻辑中有一出一，我们只需要判断或者找到其中一个命题成立，这整个逻辑就成立。除此之外，每个命题都可以转化成和的形式。AB可以转化成^(^A+^B)这是基于双重否定消除（非非为本身）以及德摩根定律（^(AB) = ^A+^B），(A+B)C 可以转化成AC+BC 这是根据分配率得到。

我们用和的形式表示所有逻辑门（为了简化表示，所以都转化成AB的形式）

z=(x) [^x + z][x + ^z]

z=NOT(x) [x + z][^x+^z]

z=NOR(x_1,x_2…x_n) [(^x_1+^z)(^x_2+^z)…(^x_n+^z)][x_1+x_2+…+x_n+z]

z=NAND(x_1,x_2….x_n) [(x_1+z)(x_2+z)…(x_n+z)][^x_1+^x_2+…+^x_n+^z]

z=OR(x_1,x_2…x_n) [(^x_1+z)(^x_2+z)…(^x_n+z)][x_1+x_2+…+x_n+^z]

z=AND(x1,x…x_n) [(x_1+^z)(x_2+^z)…(x_n+^z)][^x_1+^x_2+…+^x_n+z]

由于AB可以转化成和的形式，所以所有逻辑门可以转化为和的形式，也就是说所有逻辑都可以用和的形式表示

接下来是运算。

对于逻辑电路的运算，我们已知的运算就是递归重复，也就是假设输入实现得到输出。我们依旧沿用这一方法，但是，当输入过大时，这一方法工程量也会大，从而影响使用。所以我们需要寻找方法简化他。

第一个方法Boolean Constraint Propagation逻辑约束传递

我们目标是结果返回为真，对于每一个逻辑单元，由于是and逻辑，所以我们需要所有输入在逻辑单元中是真的表述，也就是对于a ^b来说a我们假设为1，b假设为0使得a为1，^b为1。这一算法会基于某一个逻辑单元所拥有的输入个数决定复杂程度

另一个方法是DPLL Algorithm DPLL算法

这一个算法并不基于和的形式，反而是基于积的形式（[A+B][^B+C]），对于这一形式，可能会存在B和B’的形式，也就是说期望某一个逻辑单元成立的同时，有其他的逻辑单元会期望另一个输入在逻辑关系中必定为1。在上面的表达式[A+B][^B+C]中，我们可以看到如果用B使得第一个单元为1，那么第二个单元的C必定为1。

我们期望的是，假设一个输入，使得更多的单元能够明确得到1或者明确依赖某一输入使得结果为1。 所以我们在选择假设输入对象时，选择在单元中出现更多的。

除此之外，基于and逻辑，有零出零。所以一旦可以确定某一单元整体结果为0，那么当前假设一定不满足SAT。

基于上述描述，我们可以得到伪代码

DPLL(clauses){
    if (clauses is a consistent set of literals){
        return true
    }
    else if(clauses contains an empty clause){
        return false
    }
    else{
        assign a popular input and DPLL(that clauses)
    }
}

上面的所有内容都是逻辑上的，接下来我们将逻辑应用到电路中。对于上面的所有逻辑，我们可以认为是如下图的电路

也可以是

第一种叫做2-level logic

第二种叫做multi-level logic

对于电路来说，我们要做的是把他转化成逻辑。也就是用A+BC这种形式表示电路逻辑。

转化的方式就是我们接下来要讨论的内容。

首先是针对2-level logic的转化

对于逻辑我们可以用BDD表示，对于电路我们用TT真值表表示。

和前面逻辑部分相似，我们只记录结果为1的输入

首先，我们必须承认表示相同结果的逻辑的表示可以是多样的，其中包括a+a’可以当作1的因素。所以我们需要明确的是我们希望转化的逻辑关系是电路表示的最简关系。

如何找到最简关系就是我们需要讨论的内容

既然需要找到逻辑关系，我们首先要明白真值表中的行列格子表示了什么。

对于ab为00的那一列来说，就是a=0，b=0的情况下的逻辑关系。

同样的对于cd的一行来说就是c=0，d=0的关系。

对于ab是00 01，cd是00 01的那一个田字格就是a=0，c=0的关系。其他的行列田字格意义类似。

其次，我们要找到一个可行的逻辑关系然后去简化。

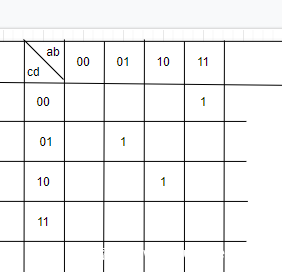
对于上图中的关系，bd同时为1且ac为0结果才为1，ac同时为1且bd为0结果才为1，ab为1cd为0结果为0。我们可以得到逻辑关系a’bc’d+ab’cd’+abc’d’

那么对于程序来说，如何获取呢。结合逻辑约束传递，首先，我们取一行存在1，且1越多越好（1越多该行优先级越高），对于该行输入逻辑，若为1则a，非1则a’。对于同块行列积运算，不同行列和运算。

接下来就是进行组合实现最优解。

也就是相当于a’bc’d+ab’cd’+abc’d’=bc’(a’d+ad’)+ab’cd’

当然也可以组合成ad’(b’c+bc’)+a’bc’d

这些组合就是期望1组合成完整田字格，除此之外还可以趋向组合成完整行列。

接下来是针对Multi-level logic

multi-level logic有更多的环节，如：f = ac+b ,g = f +a’c

我们可以将环节去掉，即直接用ac+b代替f写入g中，再次我们可以得到更简洁的表示ac+b+a’c = b+c

当然，这里还存在一种情况就是其中一个环节 f = ab+ac+ad

我们可以添加一个环节a，f = a(b+c+d)

那么我们如何使用程序实现这一目标呢。

首先我们要将逻辑和数理的关系明确：

基于前面分配律的存在，我们可以将and当作乘，or当作加。这样我们就可以使用数理计算实现逻辑and和or的计算，但是，数理并不能表示非运算，这也就使得我们必须使用新的符号表示非运算的结果，并且忽视新符号与原要素的非关系。

接下来就是寻找满足简化条件的环节以及元素。

首先是添加环节的方法：添加一个环节需要满足的条件是一个元素多次出现在和形式的逻辑单元中，如上面的例子所示。

要想知道如何用算法找到该元素必须找到该元素具有的特征：首先该元素一定在整个逻辑中出现了，也就是逻辑中的每一个元素都有可能多次出现，同时也只有逻辑中的元素才有可能。我们可以遍历尝试。（在这里我们将这个多次出现的元素集合记作divisor）

当将这一元素提出后，逻辑关系的表达式就可以变成F = D * Q + R（D就是divisor，Q是提出D元素后的逻辑的表达式，R是不包含D元素的其他逻辑的表达式集合）

for (each cube d in divisor D){
    let C = {cubes in F that comtain this product term d}
    if (C is empty){
        return (quotient = 0 ,reminder = F)
    } 
    let C = cross out literals of cube d in each cube of C
    if(d is first cube we have looked at in divisor D){
    let Q =C
    }
    else{
    Q = Q ^ C
    }
    R = F - (Q*D)
    return  (quotient = Q ,reminder = R)
}

但是，有些时候不仅仅是一个元素可以提取，可能是多个元素组合可以提取，如F = axc + axd + axe + bc + bd + de，我们可以提取ax和b然后在提取(c+d+e)最后形成(ax+b)(c+d+e)

所以在找到一个元素之后，我们依旧要对剩余逻辑表达式进行分析

FindKernels(cube-free SOP expression F){
    K = empty
    for(each variable x in F){
        if(there are at least 2 cubes in F that have variable x){
            let S = {cubes in F that have variable x in them}
            let co = cube that results from intersection of all cubes in S that will be the product of just those literals that appear in each of these cubes in S
            K = k ∨ FindKernels(F / co)
        }
    }
    K = K ∨ F
    return K
}

不知道大家有没有发现这一个方法有不足之处。

我们举一个例子：F = axc + axd + axe + bc + bd + de

我们首先提取a：a(xc+xd+xe)+bc+bd+be

然后提取x：ax(c+d+e)+bc+bd+be

之后省略。

假设我们先提取x，再提取a，结果是不是依旧一样呢。答案是是的。所以我们使用的方法存在冗余。

除此之外，对于同一个表达式有不同的提取方式，这不同的提取方式可能会造成最后结果的表达式不同

如：a’bc’d+ab’cd’+abc’d’=bc’(a’d+ad’)+ab’cd’=ad’(b’c+bc’)+a’bc’d

所以我们要找到一个最优的提取方式。

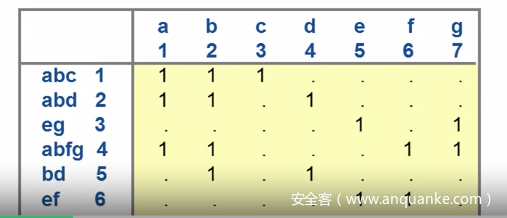
如何处理呢。我们要找到那个出现次数最多的元素进行提取，并且一次提取最多个数元素。我们先对逻辑单元进行分析记录元素出现次数。

我们可以使用如下图的形式记录

2-level logic

multi-level logic

然后先寻找元素最多的逻辑单元，依据逻辑单元中存在的元素找尽可能多符合相同存在元素的逻辑单元，一直到寻找完毕，对最终尽可能多的满足的元素提取，然后重复上述操作。

 

最后

以上就是本篇的全部内容
感谢阅读