前言
发现最近很少人看了,也收到很多师傅反馈看不懂,相关的前置知识我在理论部分也简单提过了,关于程序分析理论的前置知识实际上就是半序集,完全格,结构归纳法。除此之外,文章大部分讲的都是关于分析的语法,就是对于一段代码,你能把它转化成什么,又能得到什么约束条件使得代码分析可以计算得到一个结果。这一个系列并不是说代码审计工具怎么编写,而是对于一个程序怎么分析,知道了分析方法,对于任何语言的代码审计都会有帮助。所以每一篇文章,我都写了很多分析语法,都是一步一步慢慢做加法最终到了现在的语法。
从最开始的数据流分析的Reaching Definition对每一句代码执行前后状态描述,到描述状态改变的UD链和DU链,到对于代码块的分析,既有过程间分析,又有控制流分析,到抽象解释分析语义,到系统模型区分类型和应用处理机制,到这篇文章的拓展的系统模型和实现分析的算法。语法有很多互通,理论和书写方式有很多一致。
确实是本人学术不精没有办法达到最初分享的目的,所以今天这篇文章主要就是介绍,具体的语法并没有特别的写出,关于约束条件也没有提及,主要通过例子简单介绍这些方法是做什么的。算法部分也就是简单逻辑和伪代码。
原计划是写完这个系列,再写fuzz的一个系列,但是好像这个系列效果不是很好,所以fuzz系列我还要迟疑一会。
侧响应分析Side Effect Analysis
侧响应分析是之前分析系统的拓展,之前的分析系统不包含数值,只包括代码执行逻辑。而侧响应分析引入了变量引用,变量定义,变量更新的操作语法。实现对执行结果的分析
这是一个斐波那契数列代码转义之后的结果,一个变量r在递归函数调用执行中变化,当 z<3 时,r+1。当 z>=3 时,结果为前两项之和。
在这个例子中,我们可以看到new v=n in e的结构,这个结构表示v初值为n,作用域为e。
此外还有 !v 的结构表示调用值,v = e表示更新,e_1;e_2表示先后执行操作。
对于代码分析程序而言,遇到这样的转义结果后需要进行以下操作:记录 r 的数据类型,记录代码执行过程中 r 会进行的引用或者更新操作
也就是建立一个表格专门记录 r 的数值,记作ref(R),创建两种处理机制引用和更新,记作!R,和R=。
以上就是侧响应分析的思路,加入数值记录完善最终分析结果。
在一个程序中,会出现常数,变量,函数,函数引用,递归,代码块执行,条件语句,布尔操作等情况,我们接下来对每一种情况阐明侧响应分析的内容。
常数和变量记录类型和数值。函数记录函数返回值类型,参数类型,过程中对参数的调用和更新。函数引用记录参数数据,返回值数据,同时将函数的记录复制过来。递归记录多次函数的记录,同时,每一次函数的参数都是上一次调用的结果,从而建立联系。代码块记录每一次的操作和结果。条件语句对判断进行分析,对分支语句分别记录操作和结果
例子中有三个new in 结构,第一个结构是 new_A x = 1 in () + () ,
第二个是 new_B y= !x in (x = !y + 1; !y + 3) ,在这个结构当中,我们记录B节点,作为表名,过程中进行了引用x,赋值y,引用y,赋值x的操作,我们记录为 {!x,y:=,!yx:=},由于x,y的值保存在表格A,表格B中我们用AB代替xy。除此之外,第一个赋值y的操作实际上就是定义一个变量,所以,我们只需要创建一个新表格记录数值就可以满足操作。
最终得到{new B,!A,A:=,!B}的响应模式
第三个是new_C x = !x in (x=!x+1;!x + 1) , 在这个结构中,和上面分析过程一样,我们最终得到{new C,!A,C:=,!C}的响应模式。
那么第一个结构我们就可以得到响应模式{new A,new B,new C,!A,!B,!C,A:=,C:=}
在这个过程中,我们发现B表格的结果没有被引用,所以对于y而言,我们可以只记录y,而不用新建一个表格记录y的值,相应的,我们对转义语句进行更改,将new_B in 改成 let y = !x in ()的结构。
这就是侧响应分析的语法。
预期分析Exception Analysis
预期分析同样是对之前系统模型的拓展,一切基于之前的模型,同时又有一些新的语法,满足更多的需求。
我们可以看到上面例子中多了两个语法:raise 和 handle as in。当x<0时满足期望x-out-of-range,分析返回x-out-of-range的设定,当y<0 或者 y>x 时,满足期望y-out-of-range,分析返回y-out-of-range的设定。
我们先分析一个简单例子
这里设定的预期是正数还是负数,对于负数存在neg的处理机制,对于正数存在pos的处理机制,虽然这里并没有实际调用,但是正因为这样,我们可以简单认为exception就是一个特定条件下调用的函数。
现在我们回到第一个例子
当x<0时,调用x-out-of-range的处理机制,也就是handle部分内容:将x-out-of-range作为0。这就是预期分析。
而预期分析在代码分析程序中的应用就是当语句满足设定可能存在危险的情况时,进行预期处理,进一步分析是否存在漏洞。
域推断Region Inference
引入数据后,存储是一个问题,所以我们引入域推断的理论。
存在数据7和9,首先,我们要保存x的值为7,预先设定函数Y的返回值保存地址,预留x+y保存的地址,随后,保存y的值为9,经过计算后,只需要记录x+y的值为16。所以7,9作为缓存数据,执行完后删除,Y的返回值也只需要在执行过程中提供。
所以我们提出region_name,regions 和 region variables,并添加语法at。
上述代码可以转换成 let region_1,region_2,region_3,region_4 in (let x = (7 at region_1) in (fn_Y y => (y+x) at region_2) at region_3)(9 at region_4)
最后将缓存数据删除,只剩下 region_2,保存在r_1域中
再结合之前的系统模型,我们得到
(let x = (7 at region_1) in (fn_Y y => (!y+!x) at region_2) at region_3)(9 at region_4)
在执行过程中,引用x,y,也就是引用region_1,region_4
赋值x+y就是将x+y的值保存在region_2
也就是存在响应机制{get region_1,get region_4 ,put region_2}
算法Algorithms
工作列表算法Worklist Algorithms
首先,引入 worklist empty作为空工作列表,insert作为插入数据,extract作为删除数据。input作为输入代码,output作为分析结果。
整个过程的伪代码就是:
初始化:新建工作列表,并填充约束。
initialisation(){
W = empty
for all x コ t in S do
W = insert((x コ t),W)
Analysis[x] = 空
infl[x] = 空
for all x コ t in S do
for all x' in FV(t) do
infl[x'] = infl[x'] ∪ {x コ t}
}
更新数据:将工作列表中的约束分析,如果约束包含子约束,那么将子语句约束插入到工作列表继续分析。
Iteration(){
while W != empty do
((x コ t),W) = extract(W)
new = eval(t,Analysis)
if(Analysis[x] !コ new){
Analysis[x] = Analysis[x] ∪ new
for all x' コ t' in infl[x] do
W = insert((x' コ t'),W)
}
}
后续分析点Reverse Postorder
程序的执行并不是永远自上而下不会跳转的,也并不是不会重复执行同一句语句的,所以,我们的算法也不可以是自上而下的。因此,我们引入Reverse Postorder。
我们对extract()进行修改
W.p保存下一个分析语句所在位置,当当前语句W.c分析完毕后,分析W.p的语句
function extract(W.c,W.p){
if W.c = nil then
W.c = sort_Postorder(W.p)
W.p=空
return (head(W.c),(tail(W.c),W.p))
}
遍历循环算法The Round Robin Algorithm
在后续分析点的理论中,我们需要找到下一句分析的语句,我们使用循环查找。为了方便代码执行,我们将所有语句用序号标记,遍历所有语句,找到符合条件的那一句语句。此时,我们不需要特地标记W.p,只需要利用代码逻辑继续执行就行。
当程序没有分析完时,遍历程序所有语句作为下一句语句分析,当找到符合的语句,重复遍历分析下一句,直到分析完毕。
while change do
change = false
for i = 1 to N do
new = eval(t,Analysis)
if(Analysis[x_i] !コ new) then
change = true
Analysis[x_i] = Analysis[x_i] ∪ new
代码块遍历Interating Through Strong Components
对于循环遍历算法,我们可以增加一些关系简少遍历。比如有些语句块中不包含跳转,我们只需要按顺序分析即可。或者有些语句有着固定执行顺序。
所以我们将代码分成代码块并标记
for i = 1 to N do
start(j) = end(j) = i
while(postorder(i) = i+1){
end(j) = end(j)++
}
i = end(j) + 1
此时,我们既要对代码块之间进行分析,又要对代码块内部分析。所以更改代码为
extract(){
if W.c = nil {
W.c = start(sort(W.c)+1)
W.p = W.p \ W.c
}
return (head(W.c),tail(W.c),W.p)
}
DR@03@星盟


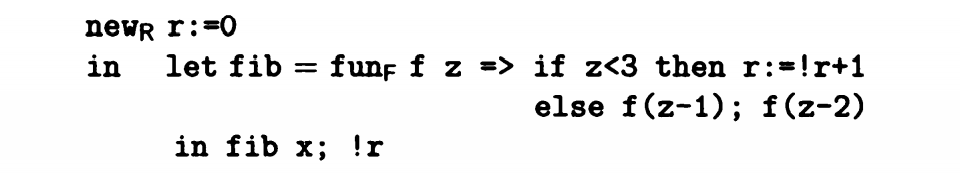
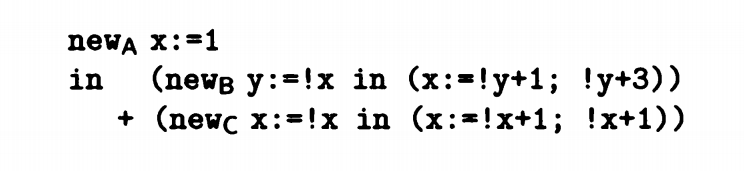
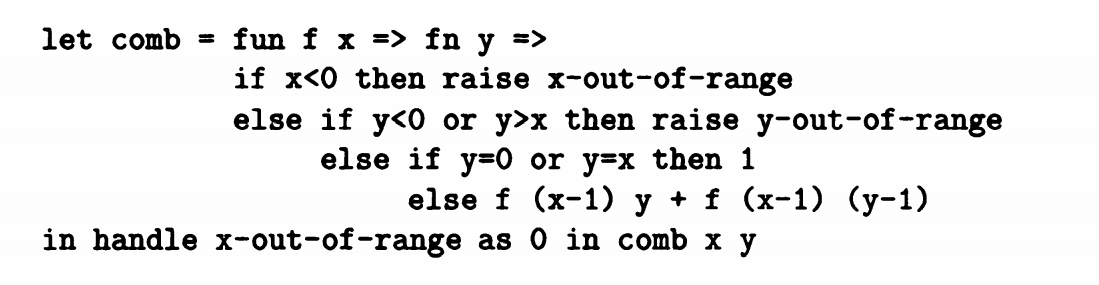
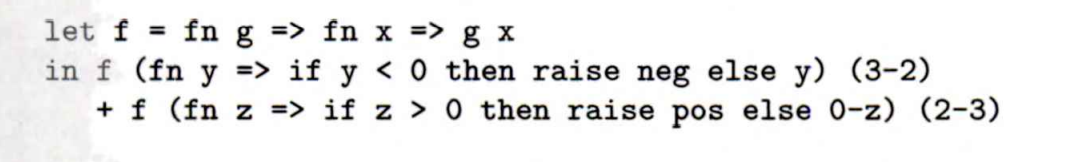
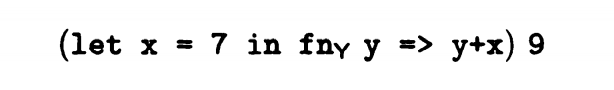







发表评论
您还未登录,请先登录。
登录