硬件安全系列 第三篇 逻辑电路基础知识介绍（三）

 

前言

这一篇是逻辑电路基础知识的最后一篇。

 

Don’t Care

Don’t Care 可以称作冗余，在电子电路中，他有不同的类型对应不同的表现形式。

首先，我们从例子的角度探索一下冗余是怎么产生的。

输入不可能

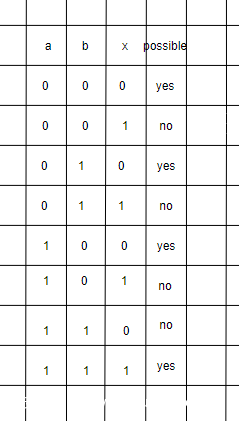
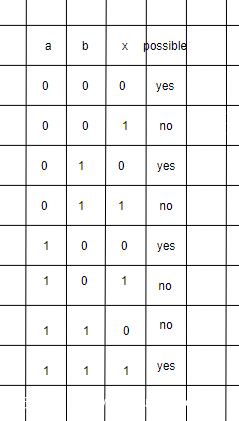
第一个例子

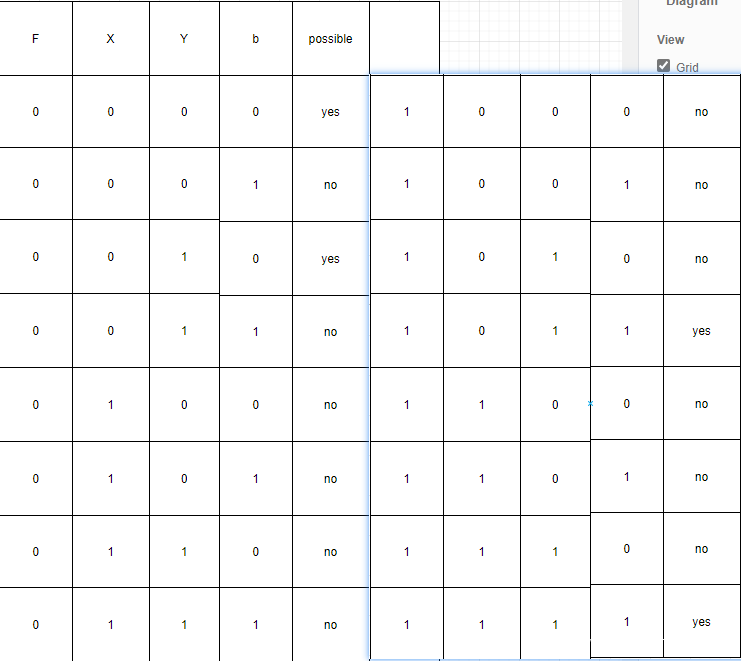
X = ab ,F = Xb + bY +XY

首先我们对于X和ab进行分析

由于X和b存在一定约束关系：X是1时，b一定是1，不能是0

所以对于F存在一些输入并不可能

这就是冗余的第一种类型：存在输入不可能在逻辑电路中出现。

那么这个don’t care冗余对F来说究竟有什么影响呢

在不考虑冗余情况下，只要X b Y 存在两个输入为1，输出就是1，现在X为1b必为1，只要X为1或者b Y 同时为1 ，输出就是1。我们也就可以把原来的逻辑关系简化成 X + bY

也就是don’t care的发现能够让我们简化电路。

所以对于我们而言，要做的就是找到冗余。

在讨论找到冗余方法之前，我们先介绍第二种冗余

输出不影响

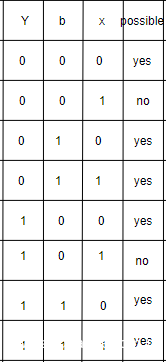
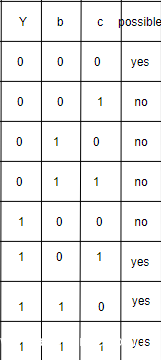
第二个例子

X = ab ,Y = b + c, F = Xb + bY + XY, Z = FXd

依旧是先寻找 X 和 ab 的关系，以及 Y 和 bc 的关系

然后是 F 和 X b Y 的关系

最后到Z = FXd

首先根据前面F和XbY的关系，我们得到X为1时，F为1，也就是不存在01的输入

接下来我们看看Z和FXd的关系，要想Z为1，FXd都要是1，也就是当Xd有一个不为1或者都不为1时，F不影响输出，而当Xd都为1时，F一定为1，也就是F从始至终都不影响输出。

这就是第二种冗余，输入对输出不影响，所以我们完全可以忽略这一输入达到简化的目的。

简化冗余

通过算法找到冗余就是我们接下来要做的事情

在讨论算法之前，我们先明确冗余的特征：在前面的两个例子中，我们分别得到的是基于对输入不可能的冗余，基于对输出无影响的冗余Observability don’t cares。

对于输入不可能存在两个方面，一个是逻辑约束Satisfiability don’t cares，另一个是环节之间的传递 Controllability don’t cares

基于逻辑约束的冗余，他的特征是在and逻辑门中，输出是1，输入必须全是1，在or逻辑门中，输出是0，输入必须全是0。也就是这里的冗余是输入所导致的输出和与其输出不符。

因此我们判断冗余的方法就是将输出X当作一个我们可以控制的输入，将原逻辑当作实际输出，当两者不等时，说明这种情况不可能出现，也就是一个冗余。

例子

X = ab + c

X xor (ab + c) = 1 的X a b c就是冗余，那么接下来就是我们的计算了，如何计算一个xor呢，在前面的SAT中，我们提到了类似的方法。我们将式子转化成CNF形式：X’ab + X’c + Xa’c’ + Xb’c’。接下来就是对每一个单元进行分析，这里我们使用Boolean Constraint Propagation逻辑约束传递的方法就可以了。

对于环节之间的传递就是当一个环节存在冗余时，他对下一个环节存在影响.那么我们怎么找到这一冗余呢。

例子

X = a + b , Y = ab , F = Xc + Yd + acd

对于 F 来说，受上一环节影响的因素只有X Y，同时F本身具有基于逻辑约束的冗余的可能，所以我们只讨论受上一环节影响，对于X Y 来说，他们具有的冗余特征是X xor (a+b) 和 Y xor ab。对于 F 来说 a 元素具有逻辑冗余的可能，所以如果在环节冗余中讨论，不得不同时考虑逻辑冗余，因此我们只对 F 中不存在的但是 X Y 中存在的 b 进行分析，分析方法就是遍历，我们需要知道对于任意b存在的冗余。

接下来是如何计算，不知道大家对任意b有没有熟悉的感觉，任意b说明b对输出无影响，在找冗余时，我们要找到对于任意b，存在一种输出是不可能出现的，对于不可能出现，其根本原因在于上一环节逻辑冗余的存在，所以我们要找的就是对于任意b依旧存在的逻辑冗余。也就可以表示为[X xor (a + b)] + [Y xor (ab)]在任意b的情况下等于1的输入组合。这里我们可以使用全部量化的方法计算，也就是计算(∨b)([X xor (a + b)] + [Y xor (ab)])

(∨b)([X xor (a + b)] + [Y xor (ab)])我们可以得到CNF的形式。

([X xor (a + b)] + [Y xor (ab)])_(b=1) = X xor 1 + Y xor a = X’ + Y’a + Ya’

([X xor (a + b)] + [Y xor (ab)])_(b=0) = X xor a + Y xor 0 = X’a + Xa’ + Y

两式求与

(X’ + Y’a + Ya’) * (X’a + Xa’ + Y)

=X’a + X’Y + X’Y’a + XYa’ + Ya’

=X’a + X’Y + Ya’

再根据Boolean Constraint Propagation逻辑约束传递的方法得到最终冗余。

除此之外，还存在另一种形式的环节之间约束的传递，那就是最初的输入存在冗余，也就是在最开始就人为规定有些输入不存在，对于这样的冗余，他不再具有逻辑性，所以我们不能用xor，此时，我们寻找另一种方法。

我们需要做的就是让之前那个计算式在冗余的输入的情况下能够返回1就可以了。既然如此，我们只需要增加冗余输入的1的形式就好了。

例子

依旧是上面的例子 X = a + b , Y = ab , F = Xc + Yd + acd

我们增加的约束是 b c d 不能同时是1

情况依旧是，对任意的b来说，存在情况满足[X xor (a + b)] + [Y xor (ab)]为1，只不过由于最初的输入限制 b c d 不能同时是1，所以在b c d 同时为1 的情况下结果也要输出1。所以我们只需要在[X xor (a + b)] + [Y xor (ab)]加上bcd，即[X xor (a + b)] + [Y xor (ab) + bcd]

计算部分和上面一样。

最后就是找到对输出无影响的冗余

对输出有影响我们可以怎么表示，使用boolean difference əf / əx

当əf / əx为1有影响，为0 无影响。

所以我们只需要计算[Z(F=0) xor Z(F=1)] 是否等于0就好了，由于我们的Boolean Constraint Propagation逻辑约束传递一般判断结果为1，所以我们在最后加上非运算。

由于F自身存在约束，所以对F 中存在的输入我们需要考虑，而对F中没有的输入，我们要求任意输入都满足。

例子

F = ab’ + a’b Z = ab + Fc’ +F’b’

(∨c)(Z(F=1) xor Z\(F=0))就是我们要计算的式子。

但是这一式子只考虑了F没有约束情况下的冗余，我们还需要做的是将F的约束情况加入，约束情况就是F xor (ab’ + a’b)，我们可以得到abF的关系，在计算过程中，将abF关系代入得到最终结果就是有约束情况的冗余。

 

最后

以上就是基础知识的全部内容