前言
本篇文章是程序分析理论部分第八篇,关于以语义为导向和基于约束的控制流分析,不仅仅有分析语义,还有部分理论证明以及最后的伪代码说明。此外,本篇文章中的例子本身在之前的文章中都出现过,虽然之前也分析过,但是这次增加了新的知识。
以语法为导向的上下文不敏感的控制流分析 Syntax Directed 0-CFA Analysis
经过上一篇的理论证明,我们得到控制流分析存在一个最小的解,但是仅仅根据上一篇文章的分析方法,我们不能利用数学的等式计算出最小解。所以我们以语法为导向得到有限约束集。使得最小解可以计算得到。
对于两个控制流分析的解,如果任意一个的最小解是另一个解的解,那么两解的公共部分一定是包含于真正的最小解之中。
例子 Example
和之前上下文不敏感的控制流分析的抽象化一样,对于let in 结构,我们可以列出这样的式子:(C , p) |= (fun f x => (f ^1(fn y => y ^2) ^3) ^4) ^5 (C , p) |= (g ^6(fn z => z ^7) ^8) ^9 C(5) 包含于 p(g) C(9) 包含于C(10)
对于fun结构,我们列出:{fun f x => (f ^1(fn y => y ^2)^3)^4}包含于C(5) 也包含于p(f) (C , p) |= (f ^1(fn y => y ^2)^3)^4
对于t_1 t_2的结构得到 (C , p) |= f ^1 (C , p) |=(fn y => y ^2)^3。
对于fn 得到{fn y => y ^2}包含于C(3) (C , p) |=y ^2
对于y ^2得到p(y) 包含于 C(2)
对于(C , p) |= (g ^6 (fn z => z ^7) ^8) ^9得到 (C , p) |= g ^6 (C , p) |= (fn z => z ^7) ^8
g为f的结果
{fn z => z ^7} 包含于 C(8) p(z) 包含于C(7)
我们可以最终得到
(C , p) |= (fun f x => (f ^1(fn y => y ^2) ^3) ^4) ^5
(C , p) |= (g ^6(fn z => z ^7) ^8) ^9
(C , p) |= (f ^1(fn y => y ^2)^3)^4
(C , p) |= f ^1
(C , p) |=(fn y => y ^2)^3
(C , p) |=y ^2
(C , p) |= g ^6
(C , p) |= (fn z => z ^7) ^8
上述式子我们可以合并成(C , p) |= (fun f x => (f ^1(fn y => y ^2) ^3) ^4) ^5 (C , p) |= (g ^6(fn z => z ^7) ^8) ^9。
接下来,我们简单证明上面的结果是代码的最小解:我们将整段代码的关系记作(C ^T, p ^T),也就是任意一句包含在这一段代码中的代码的关系(C , p)都包含在(C ^T, p ^T)中,同样的每一句代码的最小解也一定包含于(C ^T, p ^T)中。所以,当(C ^1, p ^1) 和(C ^2, p ^2)拥有一个共同的表达式满足对应关系,那么这个表达式就可以对(C ^1, p ^1) 和(C ^2, p ^2)进行共同描述。
根据上面的定理我们可以得到上述的结果是所有(C , p)的共同描述。
同时,由于(C , p)是有限的,(C , p)的任何描述的子集都在上述结果中,所以上述结果是一个摩尔集,也就是最小解。
基于约束的上下文不敏感的控制流分析Constraint Based 0-CFA Analysis
在之前的分析中,我们已经实际上已经得到了控制流的约束条件。对于上述例子就是满足
C(5) 包含于 p(g)
C(9) 包含于C(10)
f 包含于C(5) 也包含于p(f)
{fn y => y ^2}包含于C(3)
p(y) 包含于 C(2)
p(z) 包含于C(7)
也就是说控制流的约束条件就是满足(C , p) |= e_0的条件
即:(我们将C[]表示为约束条件)
C[c ^l] = 空集
C[x ^l] = {r(x) 包含于 C(l)}
C[(fn x => e_0) ^l] = {{fn x => e_0} 包含于 C(l)} C(e_0)
C[(fun f x => e_0) ^l] = {{fun f x => e_0} 包含于 C(l)} C(e_0) {{fun f x => e_0} 包含于 r(f)}
C[(t_1 ^l_1 t_2 ^l_2) ^l] = C[t_1 ^l_1] C[t_2 ^l_2] 当fn x => t_0 ^l_0在t_1中或者 fun f x => t_0 ^l_0在t_1中 时 C(l_2) 包含于 r(x) C(l_0) 包含于 C(l)
C[(if t_0 ^l_0 then t_1 ^l_1 else t_2 ^l_2) ^l] = C[t_0 ^l_0] C[t_1 ^l_1] C[t_2 ^l_2] C[l_1] 包含于 C[l] C[l_2] 包含于 C[l]
C[(let x = t_1 ^l_1 in t_2 ^l_2) ^l] = C[t_1 ^l_1] C[t_2 ^l_2] C[l_1] 包含于 r[x] C[l_2] 包含于 C[l]
C[(t_1 ^l_1 op t_2 ^l_2) ^l] = C[t_1 ^l_1] C[t_2 ^l_2]
例子Example
根据t_1 t_2的形式以及fn x => x 的形式,我们得到下面结果
C[((fn x = x ^1) ^2 (fn y => y ^3) ^4) ^5] = {
{fn x => x ^1} 包含于 C(2)
r(x) 包含于 C(1)
{fn y => y ^3} 包含于 C(4)
r(y) 包含于C(3)
左表达式包含参数,右表达式对左表达式的参数进行操作 ==> C(4) 包含于 r(x)
C(4)对y进行操作 ==> C(4) 包含于 r(y)
C(1) 包含于 C(5)
C(3) 包含于 C(5)
}
C[e_0] 和 (C , p)关系是C[e_0]是约束关系的实体,(C , p)是约束关系的逻辑表示,(C , p) |= e_0 需要满足 C[e_0] 。约束条件中的C(l) 与 (C , p)的C对应 。r(x) 与 (C , p)中的p对应。
我们对于相互转化的关系用 (C , p) [C(l)] = C(l) 和 (C , p)[r(x)] = p(x)表示。
其中对于基本类型语句t (C , p) [{t}] = {t} 对于本身是运算又会返回值参与其他运算的语句t (C , p) [{t}] 包含于 rhs’ => lhs] = (C , p) [lhs]
所以我们可以得到这样的式子 (C , p) |= C[e]
我们简单证明式子成立且为最小解: 举一个t_1 ^l_1 t_2 ^l_2的例子,l_1的运算结果会运用到t_2中所以(C_1, p_1)包含于(C_2, p_2),也就是约束条件渐渐叠加。因为(C ,p) 是有限个,所以有一个解是极限值,也就是最小解。
在实际应用中,我们可以用链表的形式记录:
对一个C[e]的约束条件,我们生成(C , p)来储存。首先进行初始化,生成空的链表,然后根据语句类型生成限制条件链以及变量,当语句为fn x => x 时将id_x保存至D[C(l)]中并且生成限制条件添加在E[q]中。当语句是其他时,生成限制条件添加在E[q]中。然后根据约束条件生成由最初的根语句对应的工作列表的解逐步演变成最终工作列表的解。即将参数id根据约束条件记录进D[C(l)]中。
我们简单证明该解为最小解:首先,对于第一步和第二步是显然有界的,第三部由于代码块有限,所以约束条件也是有终止的。所以解是可计算的。然后证明为最小解,假设(C‘ , p’) |= C[e] 那么任意D[C(l)] 包含于 C’(l)中 D[r(x)] 包含于 p’(x)中。这在第一步中实现。随后第二部中保证了对于任何形式的t p的处理使得(C , p) |= C[e]始终满足。所以该解为最小解。
根据上面的描述,我们得到以下结论:(C , p) |= C[e] 是最小解,以语法为导向和基于约束的结果是相同的,
伪代码
Init : W = nil D[q] = nil E[q] = nil
Build :
for cc in C[e] :
case cc of
{t} p : add(p,{t})
p1 p2 : E[p1] = cons(cc,E[p1])
t p => p1 p2:E[p1] = cons(cc,E[p1]) E[p] = cons(cc,E[p])
Iteration :
while W ≠ nil :
q = head(W) W = tail(W)
for cc in E[q]
case cc of
p1 p2 : add(p2,D[p1])
{t} p => p1 p2: if t ∈ D[p] then add(p2,D[p1])
最后
欢迎指教
DR@03@星盟


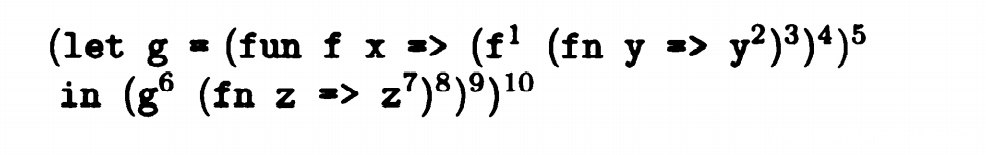
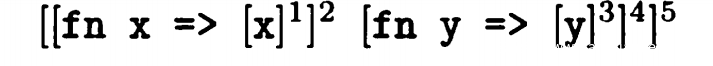







发表评论
您还未登录,请先登录。
登录