前言
程序分析理论第十篇抽象解释,从理论角度寻找分析程序的通用方法并找到数学依据使之可行。
抽象解释 Abstract Interpretation
抽象解释是使语义和分析融合的一种方法。
首先我们做出通用的基础模型。
对于一个程序,当输入是值v1时,输出必定是值v2,我们可以记作 p |- v_1 ~ v_2,对于一个程序,输入是l_1参数集合,输出点是l_2参数集合时,我们记作 p |- l_1 > l_2
接下来将之前分析的结构转化成这样的模型。
while结构包含两种操作语义: <S , σ> -> <S’ , σ’> / <S , σ> -> σ’,对于我们可以记作 S |- σ1 ~ σ2。其中σ1是程序进入点的值也是参数集合,σ2是程序退出点的值也是参数集合。所以,我们还可以记录S |- σ1 > σ2以表示在进入while循环前输入是σ1时,输出是σ2并在判断处退出。
fun结构的操作语义是p |- ie -> ie’,进行抽象解释后记作 e |- v1 ~ v2。v1是调用函数前的实参,v2是调用函数后的虚参。我们可以记录(p_1 , v_1) > (p_2 ,v_2) 用以表示在p_1参数集合中以v_1作为值时,会以p_2为参数集合中的v_2为结果。
接下来,我们将值v和参数集合l的关系记作R,当满足 p |- v_1 ~ v_2 p |- l_1 > l_2 时程序带着l_1的参数集合中的v_1值进行结构上的操作时,程序最终一定带着l_2的参数集合中的v_2值在子程序中执行代码。所以我们可以得到v_1 R l_1 & p |- v_1 ~ v_2 p |- l_1 > l_2 ——-> v_2 R l_2
除此之外,我们还可以得到当 v 是 l_1 的值且 l_1 包含于 l_2 时,v一定也是l_2参数集合中的值。当 v 是l_1 的值也是l_2 的值,那么v是l_1和l_2参数集合的交集的值。
从上面的分析来看,一个值v存在在多个参数集合当中,我们要找到对于值v来说最佳的参数集合。我们将这个对应关系表示为β()。即β(v_1) ㄈ l_1 & p |- v_1 ~ v_2 p |- l_1 > l_2 => β(v_2) ㄈ l_2 。
在这个式子当中,我们可以得到β1 和 β2存在对应关系,也就是R_1 R_2存在对应关系。
例子
plus |- (z_1,z_2) ~ z_1 +z_2
上述例子中,对于z_1 属于 Z z_2 属于 Z,求z_1 +z_2的结果集合。我们将z_1 + z_2记作 z ,原式就可以表示为plus |- (z_1,z_2) ~ z ,即存在对应关系(z_1,z_2) R ZZ -> z R Z’。为了表示未知的Z’,我们根据ZZ和Z’存在对应关系将 Z’ 记作 f (ZZ) 。
对于Z集合,我们还可以表示为{[z_1,z_2] | z_1 <z_2, z_1∈ Z ∪ {-∞} ,z_2 ∈ Z ∪{+∞}}。即Z下限为z_1上限为z_2。我们将下限表示为inf(Z),上限表示为sup(Z)。特殊的,对一个空集合,我们将它上限记作∞ 下限记作-∞。对于一个集合Z_1包含于另一个集合Z_2需要满足inf(Z_2) <= inf(Z_1) sup(Z_1) <= sup(Z_2)。
除此之外,Z集合的最小的上限就是[inf’{inf(Z)},sup’{sup[Z]}]。其中inf’{inf(Z)}是Z集合的最小值,sup’{sup(Z)}是Z集合的最大值。
对于 Z -> Z‘可能存在三种情况:到达交汇处Fix(f) = {Z | f(Z) = Z},递减Red(f) = {Z | f(Z) < Z} 递增 Ext(f) = {Z |f(Z) > Z}。其中,最小的上限Ifp(f) = ∏Fix(f) = ∏Red(f) ∈ Fix(f) 包含于 Red(f),最大的下限gfp(f) = 最小的上限Fix(f) = 最小的上限Ext(f) ∈ Fix(f) 包含于 Ext(f)。也就是lfp(f) = Red(f)和Fix(f)交汇处的最大的下限,gfp(f) = Ext(f)和Fix(f)交汇处的最小的上限。
如图所示:
但是,我们不能保证集合在递增的时候其元素就是最小交汇点的元素,也不能保证其递增到最后会趋于稳定,所以我们需要利用一个新的序列替换原来的递增集合使得存在上确界以及有一个元素等于最小交汇点元素。
为了找到这个新的序列,我们首先引入取上限的操作运算符,即对于 (l1 |^| l_2) >=l_1 (l_1 |^| l_2) >=l_2 。对于新序列,我们设定其函数对应关系为取上限,即存在 l\‘n <= ln |^| l(n+1) = l_‘n+1,所以新序列存在一个下确界为 l_0 。
对应的我们可以得到 [z_1 ,z_2] |^| [z_3,z_4] = [ LB[z_1,z_3] ,UB[z_2,z_4] ]。同时,我们要建立新序列和原序列之间的关系我们对取上限操作增加原序列限制,记作|^K|
[z_1 ,z_2] |^K| [z_3,z_4] = [ LB_K[z_1,z_3] ,UB_K[z_2,z_4] ]
即当z_1 < z_3则LB_K[z_1,z_3] = z_1当z_3<z_1 且在K中存在k<= z_3取最大k为LB_K[z_1,z_3]的结果。当 z_3 < 任意k 时结果为-∞。
当z_4 < z_2则UB_K[z_2,z_4] = z_2当z_2<z_4 且在K中存在k>= z_4取最小k为UB_K[z_2,z_4]的结果。当 z_4 > 任意k 时结果为∞。
随后我们引入取下限操作|∨| 当l_2 < l_1时,l_2 < (l_1 |∨| l_2) < l_1即使得序列最终趋向于稳定。
对于[n,∞]_n,当n > N时 [n,∞]_n = [N,∞]_N
结合上限和下限操作,我们可以得到一个满足递增或递减条件的最后总能够趋于稳定的序列。
伽罗瓦关系Galois Connection
首先,伽罗瓦关系是两个半序集之间的特定对应关系:存在两个单调函数使得两个半序集的元素形成映射。
对于原序列和新序列,我们建立两个相互为逆的抽象关系α,γ。
α : L ->M γ : M -> L
对于一个 l 我们可以在M中找到一个元素和α(l)对应,对于一个 m 我们可以在L中找到一个元素和γ(m)对应,对于γ (α(l)) 不一定是 l ,可以是 l 的近似值。
(L,α,γ,M)的关系就是伽罗瓦关系。
例子
γ_ZI([0,3]) = {0,1,2,3}
γ_ZI([0,∞]) = {z∈Z | z >=0}
α_ZI({0,1,3}) = [0,3]
α_ZI({ 2*z | z > 0}) = [2,∞]
接下来我们把伽罗瓦关系和之前的抽象解释结合起来。
伽罗瓦关系中的两个半序集分别对应数据流分析中的两个State,控制流分析中的两个closure,实际的两个集合区间。
α_sign(Z) = {sign(z) | z ∈Z}
γ_sign(S) = {z ∈Z | sign(S) ∈S}
例子 1
γ_IS({-,0,+}) = [-∞,+∞]
γ_IS({-,0}) = [-∞,0]
γ_IS({-}) = [-∞,-1]
γ_IS({+}) = [1,+∞]
γ_IS({-,+}) = [-∞,0][0,+∞]
γ_IS({0,+}) = [0,+∞]
γ_IS({0}) = [0,0]
由于伽罗瓦关系并不是满足一一对应的全射关系,所以将伽罗瓦关系应用到程序分析中时,我们需要对伽罗瓦关系进行加强,即α是满射关系,任意一个范围都可以归纳成- 0 + 的组合。γ是单射的,任意- 0 + 的组合其值唯一确定,如上面例子所示。且γ是有序的,不改变原有的数据结构和关系,如γ(m_1) 包含于 γ(m_2) 则 m_1 包含于 m_2
例子 2
diff(z_1,z_2) = |z_1| – |z_2|
α(ZZ) = {|z_1| – |z_2| |(z_1,z_2) ∈ ZZ}
γ(Z) = {(z_1,z_2) | |z_1| -|z_2| ∈ Z}
从上面的例子可以看出,M也可以是一个新的L,即对于伽罗瓦关系,存在L L_1 L_2 ……使得α(L) = L_1 γ(L_1) = L ……
也就是伽罗瓦关系适用于抽象解释当中的序列,即我们依旧可以使用取上限和取下限的操作。所以对于程序分析,我们使用伽罗瓦关系的结构能够完美适用于我们之前的理论分析并进行实际操作。
最后
水平有限,欢迎指教
DR@03@星盟


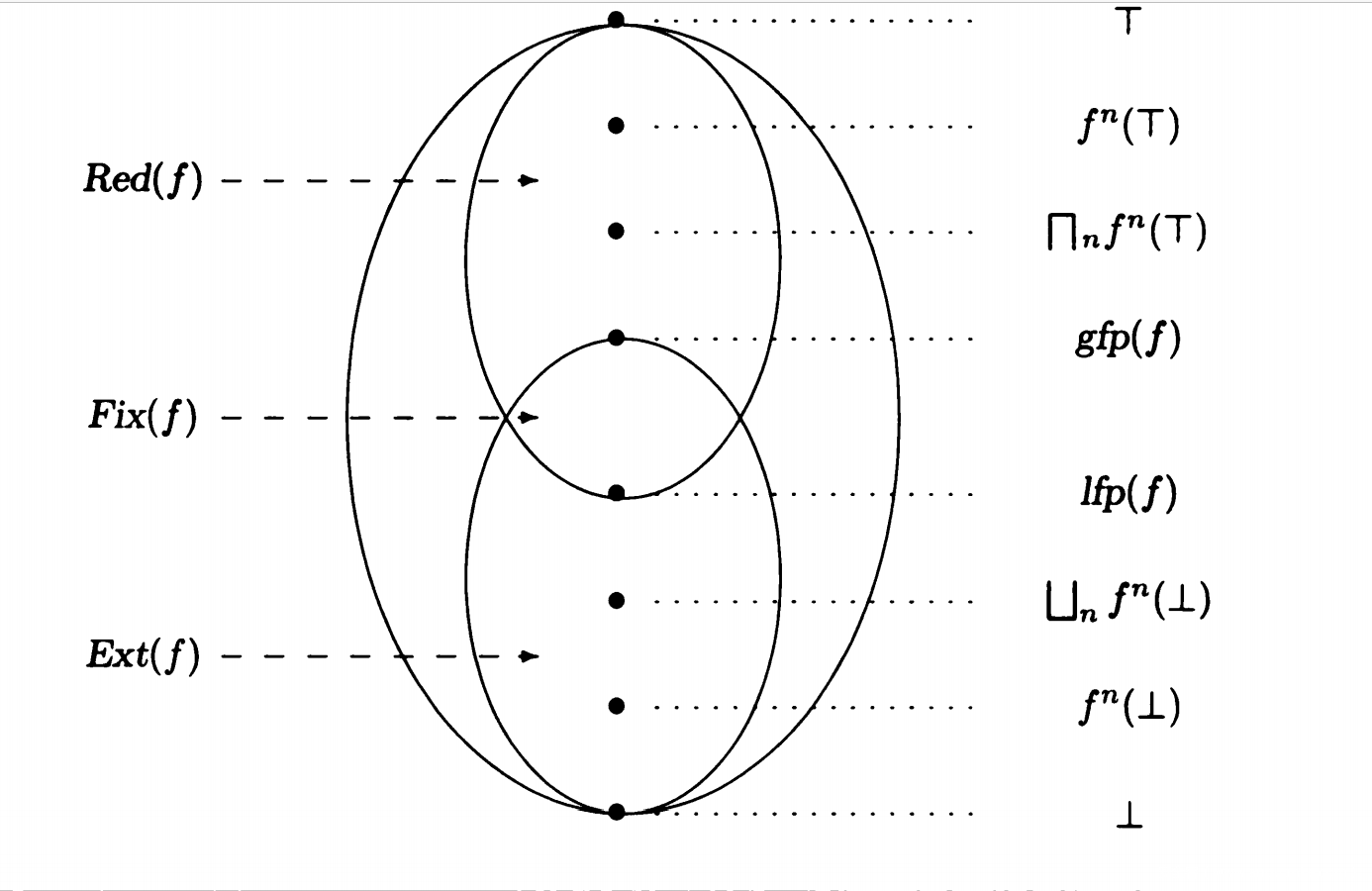







发表评论
您还未登录,请先登录。
登录