前言
到目前为止,数据流分析部分就结束了。数据流分析有一个缺陷,那就是数据流分析处理的是命令式语句:a=b或者a=b+c。而且是没有过程的命令式语句:变量参数不是一个函数的返回结果。面对有过程的命令式语句和函数式语句以及面向对象的语句,数据流分析就不能适用了。
这一篇文章讲的是控制流分析的抽象化和数学表示
控制流分析 Control Flow Analysis
我们学习新的分析方法:控制流分析
我们先对控制流分析和数据流分析进行对比:数据流分析使用了UD链,在于通过分析定义的变量和使用实现对程序的分析。控制流分析则是对程序进行抽象化后进行分析。
数据流分析中,我们有exp 和var 作为基本的组成部分构成抽象分析。在这里我们使用exp和term来作为最小单元。那么term和var有什么关系呢:在数据流分析中,我们在意的是某个变量最后的结果是什么,所以将每个变量都分开来保存,就像面向过程的编程语言一样,a=1 b=2 一个一个是独立的。然而,a和b实际上还是有关联的。就是a和b都是数字,正如面向对象的编程语言,我们将有共同点的东西归纳成一个类,term有以下几种情况:var变量,const常量,op操作符,lab标签。a可以等于x也可以等于1也可以是函数的返回值或者是一个运算的返回值或者复杂运算的结果。其中f和x表示变量var,c表示const常量,op表示OP,l表示lab标签。
因此,我们分析的最小单元是一段不包含跳转的代码块,该代码块可能是另一个代码块所需要的参数,也可能是判断是否执行某一代码块的bool类,还可能是程序的部分最终结果。
根据上述思想,我们需要记录的数据是由赋值语句决定的参数或者是一个复杂运算的结果决定的数。以及从所有抽象化后的操作找到所执行的操作。我们用C(l)将参数和一个复杂运算结果进行连接,ρ(x)将参数和操作链接。let表示抽象化后的操作,in表示包含参数的实例。
抽象后的最终分析可以用抽象代码树AST或者控制流图CFG实现。
例子 Examples
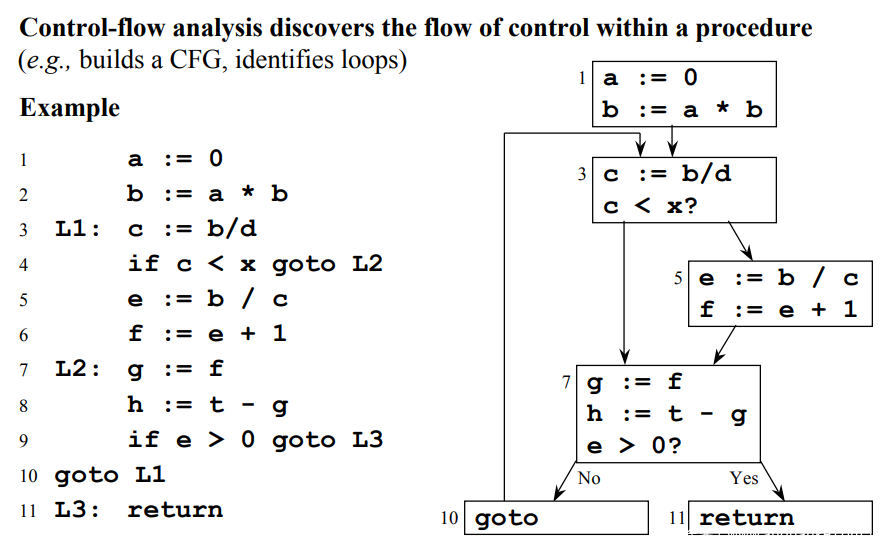
图片来自于colostate university的control-flow analysis课件
左侧是类似于汇编语言的伪代码,我们可以看到全部代码可以分为1-2 3-6 7-9 10 11五个部分,划分方法是在代码块中不存在跳转。
右侧则是左侧划分的控制流图CFG
其中需要特别关注的是1,3,7,10,11,每一个模块的起始位置。
接下来是principles of program analysis的例子
let是使用到的抽象语言,我们将=1看作f,+2看作g,+3看作h。in是实际执行语句。
那么(f g) + (f h)就是(1+2)+(1+3)
同时,我们还会发现形如(f g) 即[e_1 e_2]的式子,
我们可以结合colostate university的control-flow analysis的例子中第一个代码块,a:=0 和b:=ab。a:=0 就是e_1,b:=a\b就是e_2
在进行下一个例子之前,我们定义以下两种与函数相关的定义
fn x => e_0 是函数的抽象定义
fun f x => e_0是函数的递归表达式,在e_0中会出现 f 作为调用自身的标志
其中fun f x => (f ^1 (fn y => y ^2)^3)^4是一个递归函数。f ^1指代函数本身,(fn y => y ^2)^3是函数的内部代码抽象化表示。
再根据let 和in 划分:let部分是函数抽象定义,in部分是实例化。
(g ^6 (fn z =>z ^7)^8)^9,将 (fn z =>z ^7)^8用h表示,就可以看作(g h)^9也就是e_1 e_2的形式。
上下文不敏感的抽象控制流分析 Abstract 0-CFA Analysis
首先,我们提出抽象分析的规范:(将代码转换成数学语言)
(C,ρ) |= c ^l 即形如a:=0的代码块。这样的代码块我们不需要特别关注,因为用户不可控。
(C,ρ) |= x ^l 形如 a:=x的代码块。我们转换成ρ(x) 包含于 C(l)。也就是在标签是 l 的代码中,一定存在变量x。
(C,ρ) |= (let x = t_1 ^ l_1 in t_2 ^ l_2) ^l 也就是和上面例子类似的形式,是一系列操作之后的结果。首先由于他内部含有形如t_1 ^ l_1的式子,依旧可以用(C,ρ)表示。所以可以细化成(C,ρ) |= (let x = t_1 ^ l_1 in t_2 ^ l_2) ^l 再进行转换。除此之外,x=t_1 ^ l_1 in t_2 ^ l_2可以得到C(l_1) 包含于ρ(x) 。最后是( ) ^l 的结构我们可以得到C(l_2) 包含于C(l)
(C,ρ) |=(if t_0 ^ l_0 then t_1 ^l_1 else t_2 ^l_2) ^l就是if语句结构。同样的该结构内部含有可以更进一步分析的式子,(C,ρ) |=t_0 ^ l_0和(C,ρ) |=t_1 ^ l_1还有(C,ρ) |=t_2 ^ l_2就显而易见了。除此之外( ) ^l的结构我们可以得到C(l_1)和C(l_2) 包含于C(l)
(C,ρ) |=(fn x => t_0 ^ l_0) ^l可以转换成fn x => t_0 ^ l_0包含于C(l)同样的 (C,ρ) |=(fun f x => e_0) ^l 转换成fun f x => e_0包含于C(l)
(C,ρ) |=(t_1 ^ l_1 t_2 ^ l_2)转换成(C,ρ) |=t_1 ^ l_1 (C,ρ) |=t_2 ^ l_2。接下来是和上面不同的地方,当C(l_1)中包含fn x => t_0 ^ l_0则任意fn x => t_0 ^ l_0属于C(l_1)都可以转换成(C,ρ) |=t_0 ^ l_0,同时C(l_2)包含于ρ(x)也就是C(l_2)一定包含对x的操作。最后C(l_0) 包含于C(l)
当包含fun f x => t_0 ^ l_0,则任意fun f x => t_0 ^ l_0属于C(l_1)都可以转换成(C,ρ) |=t_0 ^ l_0,C(l_2)包含于ρ(x),C(l_0) 包含于C(l)以及{fun f x => t_0 ^ l_0} 包含于ρ(f)
接下来,我们解释一下上下文不敏感:实际上控制流分析是可以上下文敏感的,只不过上下文不敏感是其最基础的形式,我们在这一篇中只讲上下文不敏感部分,也就是只考虑目前代码块中的逻辑与数据存储。
例子 Examples
最外面的形式是[t_1 ^ l_2 t_2 ^ l_4] ^5,转换成(C,ρ) |=t_1 ^ l_2 (C,ρ) |=t_2 ^ l_4。由于t_1 ^ l_2是[fn x => [x] ^1] ^2,所以进一步转换成(C,ρ) |=[x] ^1 ,C(l_4)包含于ρ(x),C(1)包含于C(5)
接下来要拓展(C,ρ) |=t_1 ^ l_2 (C,ρ) |=t_2 ^ l_4 (C,ρ) |=[x] ^1
(C,ρ) |=t_1 ^ l_2是{fn x => [x] ^1}包含于C(2)
(C,ρ) |=t_2 ^ l_4是{fn y => [y] ^3}包含于C(4)
(C,ρ) |=[x] ^1是ρ(x)包含于C(1)
同样的对[fn y => [y] ^3] ^4我们可以得到ρ(y)包含于C(3)
总结下来就是;
C(l_4)包含于ρ(x)
C(1)包含于C(5)
{fn x => [x] ^1}包含于C(2)
{fn y => [y] ^3}包含于C(4)
ρ(x)包含于C(1)
ρ(y)包含于C(3)
{fn y => [y] ^3}包含于C(4)包含于ρ(x)包含于C(1)包含于C(5)
我们对每一部分抽象表示
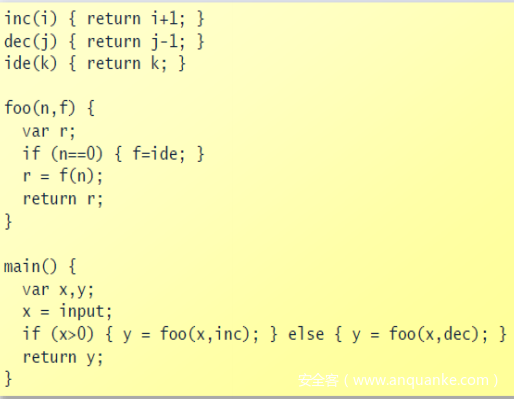
inc(i) —> fn i => i+1
dec(j) —> fn j => j-1
ide(k) —> fn k => k
foo(n,f) —> fn r=> ((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3
main() —> (fn y=> ((fn x => input ^0) ^1 (if (x>0) then y=foo(x,inc) ^2 else y=foo(x,dec) ^3) ^4) ^5) ^6
流程图就是 main —> foo —> inc/dec/ide
其中第一个跳转根据if提供不同参数,第二个跳转根据参数调用不同函数。
使用数学表达式就是
从main开始C((fn y => e_0) ^6) = {{fn y => e_0} 属于 C(6) } ∪ C[() ^5]
C([] ^5) = C([fn x => input ^0] ^1) ∪ C([if then else] ^4) ∪ {C(4) 包含于ρ(x)} ∪ {C(0) 包含于 C(5)}
C([if then else] ^4) = C(x>0) ∪ C(y=foo(x,inc) ^2) ∪ C(y=foo(x,dec) ^3) ∪{C(2) 包含于C(4)} ∪ {C(3)包含于 C(4)}
C(x>0) = C(x) ∪ C(0)
C(x ^7) = {ρ(x) 包含于 C(7)}
C(0) = 空
C( y = foo(x,inc) ^2) = C((let y = fn r=> ((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3 in fn y => ((if (x==0) f=ide) ^1 (y=f(x)) ^2) ^3 )^L) = C((fn y=> ((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3) ^L_1) ∪ C((fn y => ((if (x==0) f=ide) ^1 (y=f(x)) ^2) ^3)) ^L_2) ∪ {C(L_1) 包含于 ρ(x)} ∪ {C(L_2) 包含于 C(L)}
同理C( y = foo(x,dec) ^3) =C((let y = fn r=> ((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3 in fn y => ((if (x==0) f=ide) ^1 (y=f(x)) ^2) ^3 )^L) = C((fn y=> ((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3) ^L_1) ∪ C((fn y => ((if (x==0) f=ide) ^1 (y=f(x)) ^2) ^3)) ^L_2) ∪ {C(L_1) 包含于 ρ(x)} ∪ {C(L_2) 包含于 C(L)}
C((fn y=> ((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3) ^L_1) = C((if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3)) ∪ {(if (n==0) f=ide) ^1 (r=f(n)) ^2) ^3) ^L_1} 包含于 C(L_1)
C((if (n==0) then f=ide) ^1 (r=f(n)) ^2) ^3) ) = C((if (n==0) then f=ide) ^1) ∪ C((r=f(n)) ^2))
C((if (n==0) then f=ide) ^1) = C(n) ∪ C(0) ∪ C(f=ide)
C(n) = ρ(n) 包含于 C
C(0) = 空
C(f=ide) = 空
C((r=f(n)) ^2)) = C((let r= f() ^i in f(n) ^j )^2) = C(f()) ∪ C(f(n)) ∪ C(i)包含于 ρ(r) ∪ C(j) 包含于 C(2)
随后f()可能是inc ,dec ,ide所以C(f()) = C(inc()) ∪ C(dec()) ∪C(ide())
C(inc()) = C((fn i => i+1) ^i) = {{fn i => i ^0+1} 包含于 C(i)} ∪ {ρ(i) 包含于 C(0)}
C(dec()) =C((fn j => j-1 ^i))= {{fn j => j ^0-1} 包含于 C(i)} ∪ {ρ(j) 包含于 C(0)}
C(ide()) =C((fn k => k ^i))= {{fn k => k ^0} 包含于 C(i)} ∪ {ρ(j) 包含于 C(0)}
同理可知C((fn y => ((if (x==0) f=ide) ^1 (y=f(x)) ^2) ^3)) ^L_2),这里不再写出。
至此,对上面例子的抽象化和数学表示就全部完成了。
作者 DR@03@星盟


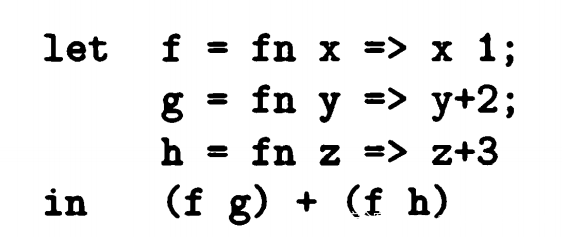
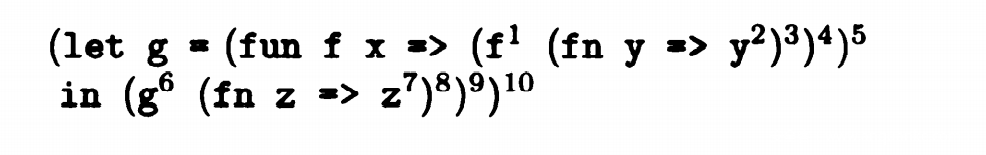
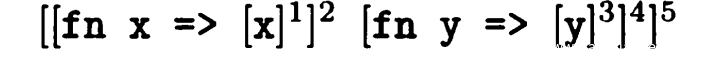







发表评论
您还未登录,请先登录。
登录